基本概念

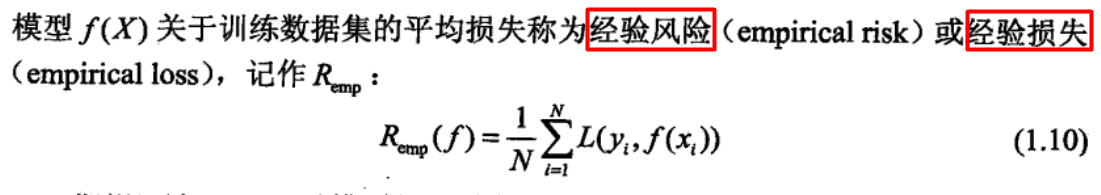
证明：

$S_{n}=\sum_{i=1}^{n}Z_{i}$

Hoeffding不等式：$P(ES_{n}-S_{n}\ge t)\le e^{-\frac{2t^{2}}{\sum(b_{i}-a_{i})^{2}}}  $

(其中$[b_{i},a_{i}]$是$Z_{i}$所属的范围，下面这个问题里设为[0,1])

$令Z_{i}=L(Y_{i},f(X_{i})),则S_{n}=\sum_{i=1}^{n}Z_{i}=\sum_{i=1}^{n}L(Y_{i},f(X_{i}))$

$E(S_{n})=nEZ=nEL(Y_{i},f(X_{i}))$带入Hoeffding不等式：

$P(nEL(Y_{i},f(X_{i}))-\sum_{i=1}^{n}L(Y_{i},f(X_{i})) \ge t) \le e^{-\frac{2t^2}{n}}$

$P(R(f)-\widehat{R}(f)\ge \frac{t}{n})\le e^{-\frac{2t^2}{n}}$

$令s=\frac{t}{n}带入即得。$