sklearn下的ROC与AUC原理详解

ROC全称Receiver operating characteristic。

定义

TPR：true positive rate，正样本中分类正确的比率，即TP/(TP+FN)，一般希望它越大越好

FPR：false negtive rage，负样本中分类错误的比率，即FP/(FP+TN)，一般希望它越小越好

ROC曲线：以FPR作为X轴，TPR作为y轴

roc_curve函数的原理及计算方式

要作ROC曲线，需要计算FPR及对应的TPR。

对于一个给定的预测概率，设定不同的阈值，预测结果会不一样。例如我们设定阈值在0.5以上的为预测正确的样本和阈值在0.3以上的结果，得到的预测就完全不同。而ROC曲线就是计算不同阈值下FPR及对应的TPR。

以https://www.w3cschool.cn/doc_scikit_learn/scikit_learn-modules-generated-sklearn-metrics-roc_curve.html?lang=en为例

>>> import numpy as np
>>> from sklearn import metrics
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
>>> fpr
array([ 0. ,  0.5,  0.5,  1. ])
>>> tpr
array([ 0.5,  0.5,  1. ,  1. ])
>>> thresholds
array([ 0.8 ,  0.4 ,  0.35,  0.1 ])

roc_curve从score中取了4个值作为阈值，用这个阈值判断，得到不同阈值下的fpr和tpr，利用fpr和tpr作出ROC曲线。

auc原理及计算方式：

AUC全称Area Under the Curve，即ROC曲线下的面积。sklearn通过梯形的方法来计算该值。上述例子的auc代码如下：

>>> metrics.auc(fpr, tpr)
0.75

roc_auc_score原理及计算方式：

在二分类问题中，roc_auc_score的结果都是一样的，都是计算AUC。

在多分类中，有两种计算方式：One VS Rest和 One VS One，在multi_class参数中分别为ovr和ovo。

ovr：以3分类为例，混淆矩阵分为3层，第一层为C1类和排除了C1的其他类，第二层为C2类和排除了C2的其他类，第三层为C3类和排除了C3的其他类，如图所示：

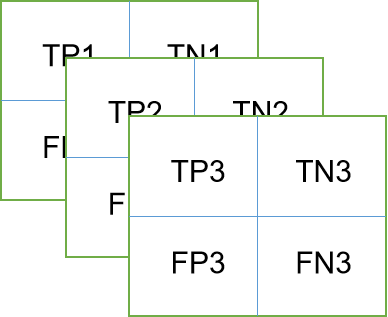
在这种情况下，需要指明如何得到总的score，sklearn的average参数有4种选择：

micro: 把所有类放在一起计算。即

$ TPR= \frac{TP1+TP2+TP3}{TP1+FN1+TP2+FN2+TP3+FN3} $

$ FPR= \frac{FP1+FP2+FP3}{FP1+TN1+FP2+TN2+FP3+TN3} $

然后以此作ROC曲线，求得score

macro: 为每一层分配相同的权值。即

$ TPR= \frac{1}{3}(\frac{TP1}{TP1+FN1}+\frac{TP2}{TP2+FN2}+\frac{TP3}{TP3+FN3}) $

$ FPR= \frac{1}{3}(\frac{FP1}{FP1+TN1}+\frac{FP2}{FP2+TN2}+\frac{FP3}{FP3+TN3}) $

weighted: 以该类在样本中占的百分比作为权重，计算TPR和FPR。

$ TPR= \frac{TP1}{TP1+FN1}w_1+\frac{TP2}{TP2+FN2}w_2+\frac{TP3}{TP3+FN3}w_3 $

$ FPR= \frac{FP1}{FP1+TN1}w_1+\frac{FP2}{FP2+TN2}w_2+\frac{FP3}{FP3+TN3}w_3 $

sample: 对于样本很不均匀的类，可以采用该方法。所以对多分类的roc_auc_score使用示例如下：

roc_auc_score(y_true, y_scores, multi_class='ovo',labels=[0,1,2],average='macro')