词向量的cbow模型

 word2vec完整的解释可以参考《word2vec Parameter Learning Explained》这篇文章。

 

cbow模型

   cbow模型的全称为Continuous Bag-of-Word Model。该模型的作用是根据给定的词$w_{input}$，预测目标词出现的概率$w_t$，对应的数学表示为 $p(w_t|w_{input})$。如下图所示，Input layer表示给定的词，${h_1,...,h_N}$是这个给定词的词向量（又称输入词向量），Output layer是这个神经网络的输出层，为了得出在这个输入词下另一个词出现的可能概率，需要对Output layer求softmax。

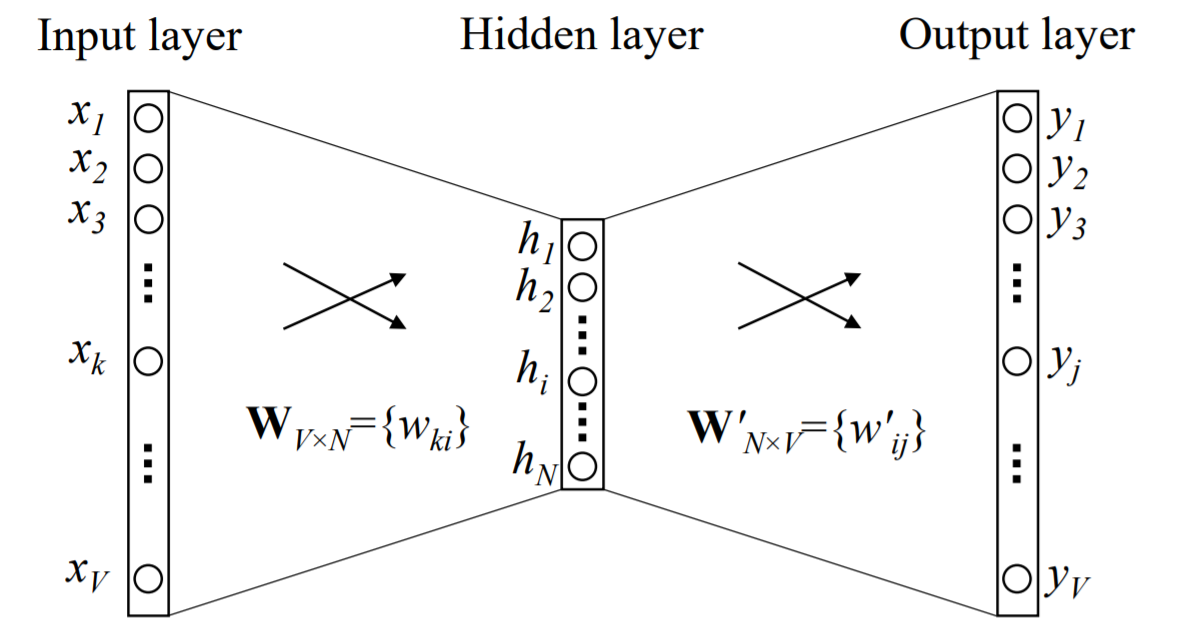
图1 单个词的CBOW模型（来源于word2vec Parameter Learning Explained）

    在cbow模型中，所有的词被编码成ont-hot向量，$V$为总词语数。input层的one-hot vector经过$W_{VXN}$矩阵后，被压缩为只有N个元素的向量$h$，之后经过$W'$矩阵出来，得到$\boldsymbol{u}$。于是根据公式，有  

$p(w_t|w_{input})=y_j=\frac{exp(u_j)}{\sum{exp(u_{j'})}}$

  最大化该条件概率，得到  

max$p(w_t|w_{input})$=max log$y_j$=$u_j$-log$\sum{exp(u_j)}$

于是得到词袋模型的Loss function:

E=-log$p(w_t|w_{input})$=log$\sum{exp(u_j)}$-$u_j$

这里，$u_j$表示第j个词向量。有了loss function,我们就可以很容易的利用各类框架进行词向量的训练了。

但是！在实际中，一个词的上下文有许多的词，往往我们需要的是，给定多个词，预测缺失词出现的概率。我们希望词袋模型能够处理这个问题。于是，为了利用之前的词袋模型，人们提出了新的解决方案。它的思路是这样的：它利用输入上下文词向量的平均与输入层到隐藏层权重的积作为输入，上下文词向量的平均作为输出。

$h=\frac{1}{C} W^T (x_1+x_2+...+x_C)$

利用之前得到的词向量，上面的公式可以简化为：

$h=\frac{1}{C}  (v_1+v_2+...+v_C)$

这里每个$v$代表了之前单个词的CBOW模型的输入词向量。

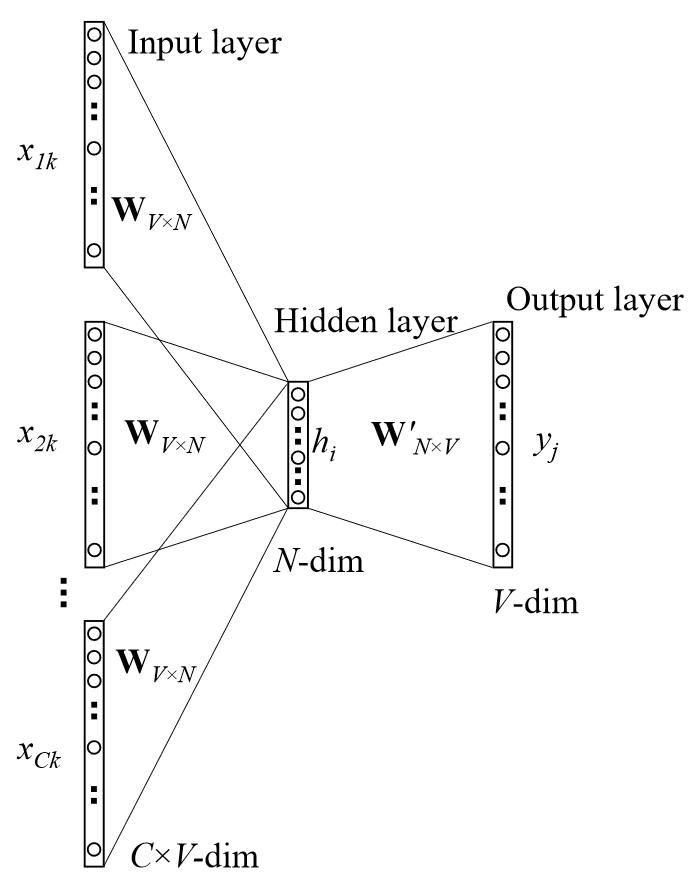
图2 多个词上下文的词袋模型