机器人关节空间轨迹规划--S型速度规划

• 关节空间 VS 操作空间

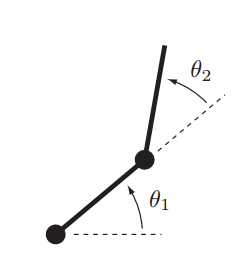
　　关节空间与操作空间轨迹规划流程图如下（上标ii和ff分别代表起始位置initial和目标位置final）：

 

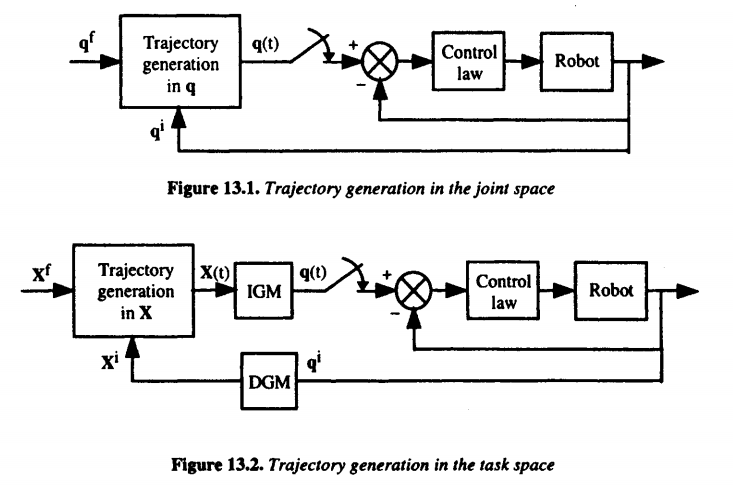
　　在关节空间内进行轨迹规划有如下优点：

1. 在线运算量更小，即无需进行机器人的逆解或正解解算
2. 不受机器人奇异构型影响
3. 可以根据机器人或驱动器手册直接确定最大速度或力矩

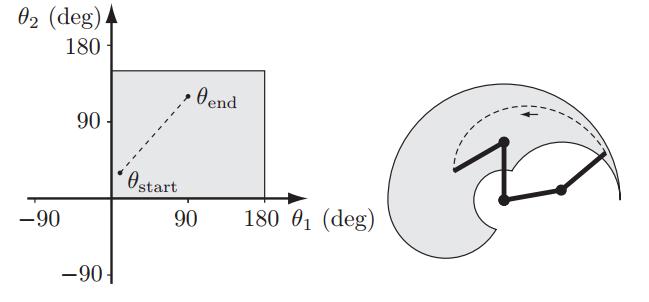
其缺点是对应操作空间的轨迹无法预测，增加了机械臂与环境碰撞的可能。例如，考虑下面的二连杆机构，关节运动的限制为：0∘≤θ1≤180∘0∘≤θ1≤180∘，0∘≤θ2≤150∘0∘≤θ2≤150∘

 　　下图中，左侧为关节空间内规划的线性运动轨迹，而其对应在操作空间的轨迹却是弧线。机构末端的可达空间在图中由灰色背景表示，其大小和形状受关节运动范围的影响。

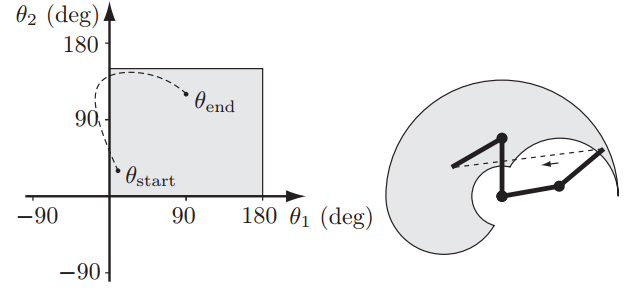
 　　下图在操作空间中规划了一条直线轨迹，其对应的关节空间轨迹为一弧线，且在运动过程中超出了关节值限制。操作空间内进行轨迹规划优点是直观，缺点是计算量大（需要计算逆解），会遇到奇异性问题以及关节运动超限等。

　　到底是选择在关节空间还是操作空间内进行轨迹规划，取决于任务需要。需要考虑避障或必须沿特定轨迹运动时选择操作空间轨迹规划，只需考虑速度、力矩、关节范围等运动约束时选择关节空间轨迹规划（The joint space scheme is appropriate to achieve fast motions in a free space）。

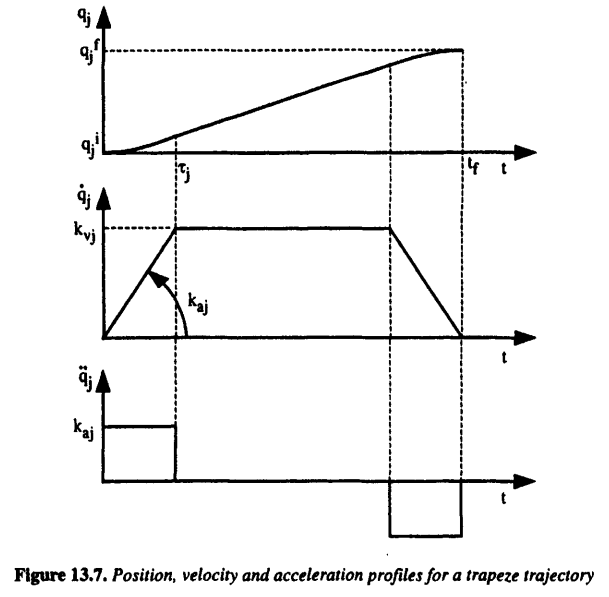
• 梯形速度曲线

　　运动控制系统中常用的梯形速度曲线如下图所示，会出现加速度不连续的情形（从kajkaj到0的跳变），这样可能会导致机械系统出现冲击或不可预料的振动，不过由于机械系统存在一定的弹性并不是绝对刚体，这种加速度不连续造成的冲击会被机械机构滤除或减轻。而对于高速重载的机器人来说，这种加速度不连续造成的影响就不能忽略了。可以参考知乎上这个问题：多轴插补为什么普遍使用梯形速度曲线？

•  S型速度曲线

 　　为了使加速度连续，可对梯形速度规划中的加速度曲线进行修改，使加速度曲线变为连续的二次曲线(a)或者梯形曲线(b)，如下图所示。其中，τ′τ′为加速段时间，λjkvjλjkvj为第jj个关节的最大运动速度

 

　　下面考虑a方法（Linear Trajectory with Polynomial Blends），关节jj的运动边界条件如下，即关节jj初始时刻位置为qijqji，初始速度加速度为0，τ′τ′时刻加速到最大速度λikvjsign(Di)λikvjsign(Di)，kvjkvj为理论上关节jj允许的最大速度，λjλj为一比例系数（0≤λj≤10≤λj≤1），DjDj为从起始位置到目标位置的位移，它是一个有正负的数值。

 

　　根据边界条件加速度二次曲线表达式为：k(t−τ′)tk(t−τ′)t，对其进行积分，可得qj˙(t)=16k(2t−3τ′)t2+Cqj˙(t)=16k(2t−3τ′)t2+C，根据速度边界条件可知C=0C=0，k=−6τ′3λjkvjk=−6τ′3λjkvj。于是推算出加速度、速度、位置的表达式分别为：

⎧⎩⎨⎪⎪⎪⎪qj(t)=qij−1τ′3λjkvjsign(Dj)(12t−τ′)t3qj˙(t)=−1τ′3λjkvjsign(Dj)(2t−3τ′)t2qj¨(t)=−6τ′3λjkvjsign(Dj)(t−τ′)t{qj(t)=qji−1τ′3λjkvjsign(Dj)(12t−τ′)t3qj˙(t)=−1τ′3λjkvjsign(Dj)(2t−3τ′)t2qj¨(t)=−6τ′3λjkvjsign(Dj)(t−τ′)t

 

　　加速度在t=τ′/2t=τ′/2时最大，其幅值为∣∣q¨jmax∣∣=32λjkvjτ′=υjkaj|q¨jmax|=32λjkvjτ′=υjkaj，则有：

τ′=32λjkvjυjkajτ′=32λjkvjυjkaj

 

　　根据上式和qj(t)qj(t)的表达式，可以计算出加速阶段的位移为：

|qij−qj(τ′)|=34(λjkvj)2υjkaj|qji−qj(τ′)|=34(λjkvj)2υjkaj

 

　　速度曲线与时间轴围成的面积为|Dj||Dj|，根据计算可以得到关系式：

t′f=τ′+|Dj|λjkvjtf′=τ′+|Dj|λjkvj

 

　　在加速度为0的阶段（最大速度阶段，τ′≤t≤τ′+h′τ′≤t≤τ′+h′），关节速度表达式为：

qi(t)=qj(τ′)+(t−τ′)λjkvjsign(Dj)qi(t)=qj(τ′)+(t−τ′)λjkvjsign(Dj)

 

　　减速阶段与加速阶段对称(t′f=2τ′+h′tf′=2τ′+h′)，减速阶段在时间段τ′+h′≤t≤t′fτ′+h′≤t≤tf′上的轨迹为：

⎧⎩⎨⎪⎪⎪⎪qj(t)=qfj+12[1τ′3(t−3τ′−h′)(t−τ′−h′)3+(2t−3τ′−2h′)]λjkvjsign(Dj)qj˙(t)=[1τ′3(2t−5τ′−2h′)(t−τ′−h′)2+1]λjkvjsign(Dj)qj¨(t)=6τ′3(t−2τ′−h′)(t−τ′−h′)λjkvjsign(Dj){qj(t)=qjf+12[1τ′3(t−3τ′−h′)(t−τ′−h′)3+(2t−3τ′−2h′)]λjkvjsign(Dj)qj˙(t)=[1τ′3(2t−5τ′−2h′)(t−τ′−h′)2+1]λjkvjsign(Dj)qj¨(t)=6τ′3(t−2τ′−h′)(t−τ′−h′)λjkvjsign(Dj)

 

　　如果目标点距离初始位置过近，可能达不到最大速度和加速度就要开始减速，考虑以最大速度做匀速直线运动阶段的时间为0这种临界状态（The minimum time tftf is obtained when the parameters λjλj and υjυj are the largest），为了能以最大速度运动，位移|Dj||Dj|必须满足如下条件：

|Dj|>32k2vjkaj|Dj|>32kvj2kaj

　　如果该条件不能满足，则最大速度值应为：

k′vj=23|Dj|kaj−−−−−−−√kvj′=23|Dj|kaj

　　前面的计算都只考虑单轴运动的情况，当需要多轴同步时，要考虑运动时间最长的轴（与每个轴的最大速度、运动位移等因素有关），将该时间作为同步运动的时间。在确定了同步时间之后，需要重新计算速度曲线的最大速度（运动快的轴要降低最大速度等待慢的轴），使得各轴在同一时刻到达设定的目标位置。

 

　　参考《Modeling Identification and Control of Robots》的第 13.3.4节 Continuous acceleration profile with constant velocity phase 以及 libfranka MotionGenerator，修改关节空间轨迹规划代码，并在while循环中进行轨迹生成的模拟。

　　traj.h

 

 　　traj.cpp

 

　　main.cpp

 

　　注意以下几点：

　　1. 原examples_common.h代码中的ddq_max_start_为加速度，ddq_max_goal_为减速度（接近目标点，开始减速），大多数情况下两者相等

　　2. 在根据速度曲线与时间轴围成的面积计算最大同步速度的时候，会遇到一元二次方程a⋅v2sync+b⋅vsync+c=0a⋅vsync2+b⋅vsync+c=0求解的问题，对于大于零的两个解要选其中数值小的那个，否则会超过最大速度限制，即取值为−b−b2−4ac√2a−b−b2−4ac2a。可以简要证明如下：

　　这两个解分布在v=−b2av=−b2a的两侧，而−b2a=tfka3=13(32kvka+|Dj|kv)ka=12kv+12(2|Dj|ka3kv)−b2a=tfka3=13(32kvka+|Dj|kv)ka=12kv+12(2|Dj|ka3kv)，根据|Dj||Dj|的条件 2|Dj|ka3kv−kv=13kv(2|Dj|ka−3k2v)>02|Dj|ka3kv−kv=13kv(2|Dj|ka−3kv2)>0，因此−b2a>kv−b2a>kv，即值较大的解会超出速度限制。

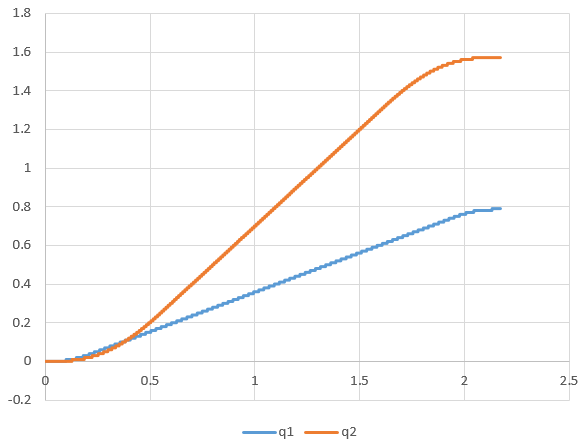
 　　将时间、轴1轴2的关节角度和速度保存在CSV文件中，用Excel画出散点图。关节角度随时间变化曲线如下（轴1从0→45°，轴2从0→90°）：

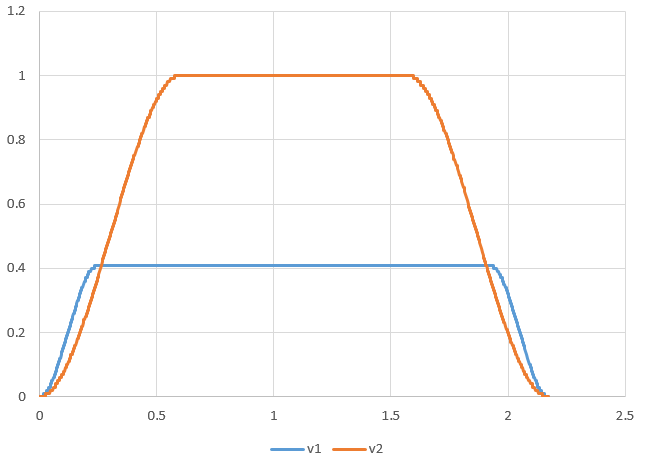
　　关节速度随时间变化曲线如下：

 

 

 

参考：

S型速度规划

线性轨迹的抛物线过渡（梯形加减速）

工业机器人运动轨迹规划方法简述

机器人中的轨迹规划（Trajectory Planning ）

周期同步位置模式(CSP)，轮廓位置模式(PPM)，位置模式(PM)

libfranka MotionGenerator

Robot and interface specifications

Trajectory Planning for Automatic Machines and Robots

Modeling Identification and Control of Robots. 13.3.4 Continuous acceleration profile with constant velocity phase

 

标签: 机器人学, 运动控制