c_pat_树题大杂烩(利用性质)
It Is Complete Binary Tree
第一行包含整数 N,表示树的结点个数。
树的结点编号为 0∼N−1。
接下来 N 行,每行对应一个结点,并给出该结点的左右子结点的编号,如果某个子结点不存在,则用 - 代替。
输出格式
如果是完全二叉树,则输出 YES 以及最后一个结点的编号。
如果不是,则输出 NO 以及根结点的编号。
思路
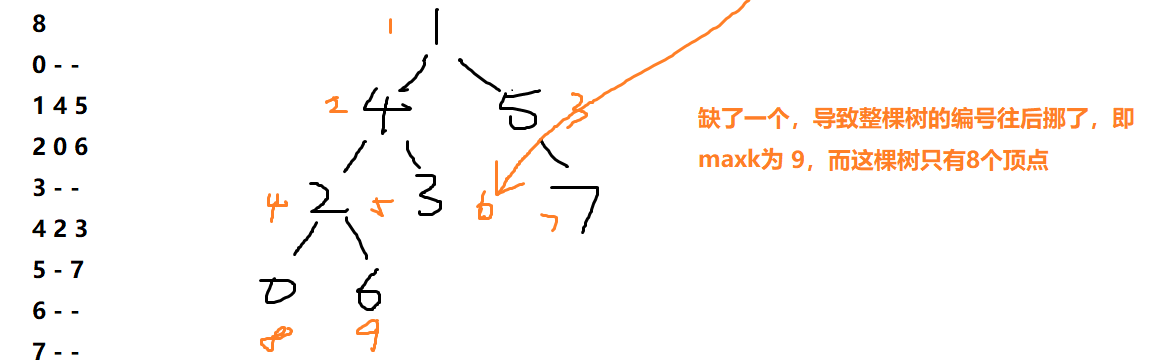
这里千万不要被题目给定的结点标号弄混淆(给的仅仅是一个编号而已),这里考的是完全二叉树的性质:如果这棵树是完全二叉树,则从上至下,再从左到右一定不会有空隙;
#include<bits/stdc++.h>
using namespace std;
const int N=25;
struct node {
int l=-1,r=-1;
} A[N];
int maxk, last_node, has_fa[N];
void dfs(int root, int k) {
if (k>maxk) {
last_node=root;
maxk=k;
}
if (A[root].l!=-1) dfs(A[root].l, 2*k);
if (A[root].r!=-1) dfs(A[root].r, 2*k+1);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
for (int i=0; i<n; i++) {
string l,r; cin>>l>>r;
if (l!="-") A[i].l=stoi(l), has_fa[stoi(l)]=1;
if (r!="-") A[i].r=stoi(r), has_fa[stoi(r)]=1;
}
int root=0;
while (has_fa[root]) root++;
dfs(root, 1);
if (maxk>n) cout<<"NO"<<' '<<root;
else cout<<"YES"<<' '<<last_node;
return 0;
}
Tree Traverse
现在给出它的后序遍历和中序遍历,请你输出它的层序遍历。
思路
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int n, post[N], in[N];
unordered_map<int, int> mp;
struct node {
int val;
node *left, *right;
};
node* dfs(int inL, int inR, int postL, int postR) {
if (postL>postR) return NULL;
int k=mp[post[postR]], lsz=k-inL;
node* root=new node();
root->val=post[postR];
root->left=dfs(inL, k-1, postL, postL+lsz-1);
root->right=dfs(k+1, inR, postL+lsz, postR-1);
return root;
}
void bfs(node* root) {
queue<node*> q; q.push(root);
int c=0;
while (!q.empty()) {
for (int i=q.size(); i>0; i--) {
auto now=q.front(); q.pop();
cout<<now->val;
if (c++!=n-1) cout<<' ';
if (now->left!=NULL) q.push(now->left);
if (now->right!=NULL) q.push(now->right);
}
}
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n;
for (int i=0; i<n; i++) cin>>post[i];
for (int i=0; i<n; i++) cin>>in[i], mp[in[i]]=i;;
bfs(dfs(0, n-1, 0, n-1));
return 0;
}
Is It a Binary Search Tree
现在,给定一个整数序列,请你判断它是否可能是某个二叉搜索树或其镜像进行前序遍历的结果。
思路
将整个序列排序,默认其为中序遍历的结果,然后用该序列和先序遍历检查是否是一颗BST;题中所说的镜像无非是将BST的性质反转:BST左子树各节点≥根结点,右子树<根节点,这只需要将中序遍历的结果逆序在检查一遍即可
注:镜像的时候,在中序序列找根应该是从右往左找,为什么?因为序列中会有重复元素,而镜像的做左子树都应≥root_val,所以从右往左找第一个不小与root_val的就是根的位置
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int c, post[N], pre[N], in[N];
bool dfs(int preL, int preR, int inL, int inR, int isMirror) {
if (preL>preR) return true;
int root_val=pre[preL], root_pos;
if (!isMirror) { //如果不是镜像,则[inL, root_pos]是左子树
for (root_pos=inL; root_pos<=inR; root_pos++) if (in[root_pos]==root_val)
break;
if (root_pos>inR) return false;
} else { //如果是镜像,为了方便递归,root_pos应该从右往左找(会有重复元素),此时[inL, root_pos]还是镜像后的左子树
for (root_pos=inR; root_pos>=inL; root_pos--) if (in[root_pos]==root_val)
break;
if (root_pos<inL) return false;
}
int lsz=root_pos-inL;
if (!dfs(preL+1, preL+lsz, inL, root_pos-1, isMirror) || !dfs(preL+lsz+1, preR, root_pos+1, inR, isMirror)) return false;
post[c++]=root_val;
return true;
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
for (int i=0; i<n; i++) cin>>pre[i], in[i]=pre[i];
sort(in, in+n);
if (dfs(0, n-1, 0, n-1, false)) {
cout<<"YES\n";
for (int i=0; i<n; i++) {
if (i==n-1) cout<<post[i];
else cout<<post[i]<<' ';
}
} else {
c=0; reverse(in, in+n);
if (dfs(0, n-1, 0, n-1, true)) {
cout<<"YES\n";
for (int i=0; i<n; i++) {
if (i==n-1) cout<<post[i];
else cout<<post[i]<<' ';
}
} else cout<<"NO";
}
return 0;
}
Complete Binary Search Tree
完全二叉树 (CBT) 定义为除最深层外的其他层的结点数都达到最大个数,最深层的所有结点都连续集中在最左边的二叉树。
现在,给定 N 个不同非负整数,表示 N 个结点的权值,用这 N 个结点可以构成唯一的完全二叉搜索树。
请你输出该完全二叉搜索树的层序遍历。
思路
已知CBT的中序遍历序列(排个序就是了)和结点的权值,求这棵CBT的层序遍历;完全二叉树的性质:假设根节点编号为k(k从0开始,假如从1开始又会不同):
- 左节点为 2k+1
- 右节点为 2k+2
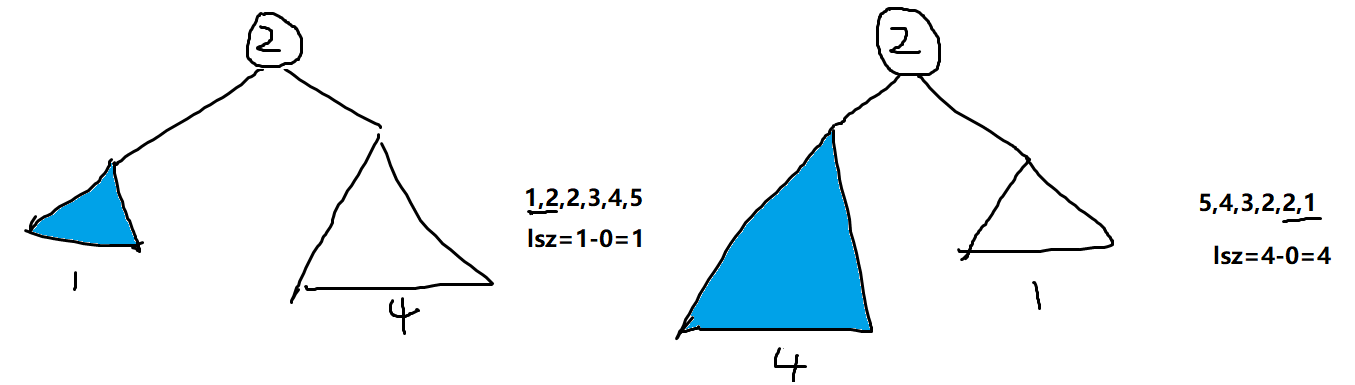
你按照中序遍历的方法遍历到左子树的最后一个结点时,此时的结点标号k对应的权值就应该是中序遍历的第一个结点的权值
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n, i, w[N], level[N];
void in_order(int k) {
if (k>=n)
return;
in_order(2*k+1);
level[k]=w[i++];
in_order(2*k+2);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n;
for (int i=0; i<n; i++) cin>>w[i];
sort(w, w+n);
in_order(0);
for (int i=0; i<n; i++) {
if (i==n-1) cout<<level[i];
else cout<<level[i]<<' ';
}
return 0;
}
Build A Binary Search Tree
N,表示树的结点个数。所有结点的编号为 0∼N−1,并且编号为 0 的结点是根结点。
接下来 N 行,第 i 行(从 0 计数)包含结点 i 的左右子结点编号。如果该结点的某个子结点不存在,则用 −1 表示。
最后一行,包含 N 个不同的整数,表示要插入树中的数值。
输出结果树的层序遍历序列。
思路
中序遍历+bfs
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n, i, c, W[N];
struct node {
int l,r,w;
} A[N];
void inorder(int root) {
if (A[root].l!=-1) inorder(A[root].l);
A[root].w=W[i++];
if (A[root].r!=-1) inorder(A[root].r);
}
void bfs(int root) {
queue<int> q; q.push(root);
while (!q.empty()) {
for (int i=q.size(); i; i--) {
int now=q.front(); q.pop();
if (c++==n-1) cout<<A[now].w;
else cout<<A[now].w<<' ';
if (A[now].l!=-1) q.push(A[now].l);
if (A[now].r!=-1) q.push(A[now].r);
}
}
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n;
for (int i=0; i<n; i++) cin>>A[i].l>>A[i].r;
for (int i=0; i<n; i++) cin>>W[i];
sort(W, W+n);
inorder(0);
bfs(0);
return 0;
}
Tree Traversals Again
通过使用栈可以以非递归方式实现二叉树的中序遍历。
例如,假设遍历一个如下图所示的 6 节点的二叉树(节点编号从 1 到 6)
则堆栈操作为:push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop()
我们可以从此操作序列中生成唯一的二叉树。你的任务是给出这棵树的后序遍历。
思路
迭代模拟中序遍历过程中的push序列就是树的先序遍历的结果;pop序列就是树的中序遍历的结果;
有了先、中序遍历结果就可以递归得到后序遍历
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int p, post[N];
vector<int> pre, in;
void dfs(int preL, int preR, int inL, int inR) {
if (preL>preR) return;
int rv=pre[preL], rp;
for (int k=inL; k<=inR; k++) if (in[k]==rv) {
rp=k;
break;
}
int lsz=rp-inL;
dfs(preL+1, preL+lsz, inL, rp-1);
dfs(preL+lsz+1, preR, rp+1, inR);
post[p++]=rv;
}
int main() {
int n; scanf("%d\n", &n);
stack<int> st;
for (int i=0; i<2*n; i++) {
string input,a,b;
getline(cin, input);
stringstream ss(input);
ss>>a>>b;
if (a=="Push") {
st.push(stoi(b));
pre.push_back(stoi(b));
} else {
in.push_back(st.top());
st.pop();
}
}
dfs(0,n-1,0,n-1);
for (int i=0; i<n; i++) {
printf("%d", post[i]);
if (i!=n-1) printf(" ");
}
return 0;
}
Counting Nodes in a BST
将一系列数字按顺序插入到一个空的二叉搜索树中,然后,请你计算结果树的最低两层的结点个数。
思路
考察二叉搜索树的建树过程;注:如果是值传递的方式传递root,那么每次都要给root赋值
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int maxd, cnt[N];
struct node {
int val;
node *right, *left;
node(int v, node* l, node* r) {val=v, left=l, right=r;}
};
node* build(node* root, int v) {
if (root==NULL) {
root=new node(v,NULL,NULL);
} else if (v<=root->val) {
root->left=build(root->left, v);
} else {
root->right=build(root->right, v);
}
return root;
}
void get_dep(node* root, int d) {
if (root==NULL) {
maxd=max(maxd,d);
return;
}
cnt[d]++;
get_dep(root->left,d+1);
get_dep(root->right,d+1);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
node* root=NULL;
for (int i=0; i<n; i++) {
int v; cin>>v;
root=build(root,v);
}
get_dep(root,0);
printf("%d + %d = %d", cnt[maxd-1], cnt[maxd-2], cnt[maxd-2]+cnt[maxd-1]);
return 0;
}
Pre- and Post-order Traversals
假设一个二叉树上所有结点的权值都互不相同。
我们可以通过后序遍历和中序遍历来确定唯一二叉树;也可以通过前序遍历和中序遍历来确定唯一二叉树。
但是,如果只通过前序遍历和后序遍历,则有可能无法确定唯一二叉树。
现在,给定一组前序遍历和后序遍历,请你输出对应二叉树的中序遍历序列之一。
思路
如果推出来的这棵树唯一,则一定有先序遍历的第2个结点和后序遍历的倒数第2个结点不同,为什么?因为如果相同的话,左子树也可能是右子树(方案一:左子树为空时,先序遍历pre[2]=post[-2];方案二:右子树为空时,pre[2]=post[-2],所以方案立马可确定为不唯一)
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int p, isUnique=1, pre[N], post[N], in[N], mp[N];
struct node {
int val;
node *left, *right;
node(int v) {val=v;}
node(int v, node* l, node* r) {val=v, left=l, right=r;}
};
node* build(int preL, int preR, int postL, int postR) {
if (preL==preR) return new node(pre[preL]);
int rv=pre[preL];
node* root=new node(rv, NULL, NULL);
if (pre[preL+1]==post[postR-1]) {
root->left=build(preL+1, preR, postL, postR-1), isUnique=false;
} else {
int pos=mp[pre[preL+1]], lsz=pos-postL+1; //找到rv的子树的根的位置
root->left=build(preL+1, preL+lsz, postL, pos);
root->right=build(preL+lsz+1, preR, pos+1, postR-1);
}
return root;
}
void inOrder(node* root) {
if (root==NULL) return;
inOrder(root->left);
in[p++]=root->val;
inOrder(root->right);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
for (int i=0; i<n; i++) cin>>pre[i];
for (int i=0; i<n; i++) cin>>post[i], mp[post[i]]=i;
auto root=build(0,n-1,0,n-1);
inOrder(root);
cout << (isUnique ? "Yes" : "No") << '\n';
for (int i=0; i<p; i++) {
cout<<in[i];
if (i!=p-1) cout<<' ';
}
cout<<'\n';
return 0;
}
Heaps
如果 P 是 C 的父结点,则在大顶堆中 P 结点的权值大于或等于 C 结点的权值,在小顶堆中 P 结点的权值小于或等于 C 结点的权值。
一种堆的常见实现是二叉堆,它是由完全二叉树来实现的。你的任务是判断给定的完全二叉树是否是堆。
思路
二叉堆是基于满二叉树构建的,所以可以得到一个性质:根编号为k时,左儿子为2k,右孩子为2k+1(k≥1),我们只需要利用该性质后遍历这棵树时比较每个结点的根和左右孩子的大小即可
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int a[N], m, n, isMaxHeap, isMinHeap;
vector<int> post;
void dfs(int k) {
if (k!=1) {
if (a[k/2]>a[k]) isMaxHeap=1;
else if (a[k/2]<a[k]) isMinHeap=1;
}
if (2*k<=n) dfs(2*k);
if (2*k+1<=n) dfs(2*k+1);
post.push_back(a[k]);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>m>>n;
while (m--) {
for (int i=1; i<=n; i++) cin>>a[i];
dfs(1);
if (isMaxHeap && isMinHeap) cout<<"Not Heap\n";
else if (isMaxHeap) cout<<"Max Heap\n";
else if (isMinHeap) cout<<"Min Heap\n";
for (int i=0; i<post.size(); i++) {
cout<<post[i];
if (i!=post.size()-1) cout<<' ';
}
cout<<'\n', post.clear(), isMaxHeap=false, isMinHeap=false;
}
return 0;
}
LCA in a Binary Tree
给顶一棵二叉树的前序和中序遍历,且给定二叉树中的任何两个结点u,v,请你找到它们的 LCA
思路

注:这里没给结点编号的范围,默认为1~N吧...
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int m,n,in[N],pre[N],vis[N],pos[N],fa[N];
struct node {
int l,r;
}a[N];
int build(int preL, int preR, int inL, int inR) {
if (preL>preR) return 0;
int rv=pre[preL], rp=pos[rv], lsz=rp-inL;
a[rv].l=build(preL+1, preL+lsz, inL, rp-1);
a[rv].r=build(preL+lsz+1, preR, rp+1, inR);
return rv;
}
void dfs(int u) {
if (u==0) return;
fa[a[u].l]=u, dfs(a[u].l);
fa[a[u].r]=u, dfs(a[u].r);
}
int find_lca(int u, int v, int root) {
if (u==v) return u;
bool mark[N]; memset(mark, false, sizeof mark);
while (u!=0) {
mark[u]=1;
if (u==root) break;
u=fa[u];
}
while (v!=0) {
if (mark[v]) return v;
v=fa[v];
}
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>m>>n;
for (int i=0; i<n; i++) cin>>in[i], pos[in[i]]=i, vis[in[i]]=1;
for (int i=0; i<n; i++) cin>>pre[i];
int root=build(0,n-1,0,n-1);
dfs(root);
while (m--) {
int u,v; cin>>u>>v;
//两种大的情况:
if (!vis[u] && !vis[v]) printf("ERROR: %d and %d are not found.", u,v);
else if (!vis[u] && vis[v]) printf("ERROR: %d is not found.", u);
else if (vis[u] && !vis[v]) printf("ERROR: %d is not found.", v);
else {
int lca=find_lca(u,v,root);
if (lca!=u && lca!=v) printf("LCA of %d and %d is %d.", u,v,lca);
else if (lca==u && lca!=v) printf("%d is an ancestor of %d.", u, v);
else if (lca!=u && lca==v) printf("%d is an ancestor of %d.", v, u);
else printf("%d is an ancestor of %d.", u, u);
}
printf("\n");
}
return 0;
}
Infix Expression
思路
构建假树,不给出根,则先通过枚举没有父亲的结点找到根;
什么时候输出括号?肯定是在输出数据data之前输出(,在输出数据data之后输出);只要当前符号的左儿子/右儿子不空就需要输出
#include<bits/stdc++.h>
using namespace std;
const int N=25;
int isleaf[N], root=1;
struct node {
string data;
int l,r;
} a[N];
void inOrder(int u) {
if (u==-1) return;
if (u!=root && (a[u].l!=-1 || a[u].r!=-1)) printf("(");
inOrder(a[u].l);
printf("%s", a[u].data.c_str());
inOrder(a[u].r);
if (u!=root && (a[u].l!=-1 || a[u].r!=-1)) printf(")");
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
for (int i=1; i<=n; i++) {
cin>>a[i].data>>a[i].l>>a[i].r;
if (a[i].l!=-1) isleaf[a[i].l]=1;
if (a[i].r!=-1) isleaf[a[i].r]=1;
}
while (isleaf[root]) root++;
inOrder(root);
return 0;
}
Is It A Red-Black Tree(30分)
思路
后序遍历建树+检查合法性:
注:由于给定的结点编号有负数,而负号仅仅表示结点的颜色,但忽略符号后还是一棵具有BST性质的红黑树
玄学pat测评
#include<bits/stdc++.h>
using namespace std;
const int N=35;
int valid, pre[N], in[N], pos[N];
struct node {
int val;
node *left, *right;
node(int v) {val=v;}
};
node* build(int preL, int preR, int inL, int inR) {
if (preL>preR) return NULL;
int rv=pre[preL], rp=pos[abs(rv)], lsz=rp-inL;
node* root=new node(rv);
root->left=build(preL+1, preL+lsz, inL, rp-1);
root->right=build(preL+lsz+1, preR, rp+1, inR);
return root;
}
bool isBlack(node* root) {
return root==NULL || root->val>0;
}
int dfs(node* root) {
if (!valid) return 0;
if (!root) return 1;
if (!isBlack(root) && (!isBlack(root->left) || !isBlack(root->right))) valid=false;
int l=dfs(root->left);
int r=dfs(root->right);
if (l!=r) valid=false;
return l+isBlack(root);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int Q; cin>>Q;
while (Q--) {
int n; cin>>n;
for (int i=0; i<n; i++) cin>>pre[i], in[i]=abs(pre[i]);
sort(in, in+n);
for (int i=0; i<n; i++) pos[in[i]]=i;
auto root=build(0,n-1,0,n-1);
valid=isBlack(root);
dfs(root);
cout<<(valid ? "Yes" : "No")<<'\n';
}
return 0;
}
Count Leaf
给定一个家谱树,你的任务是找出其中没有孩子的成员。
第一行包含一个整数 N 表示树中结点总数以及一个整数 M 表示非叶子结点数。
接下来 M 行,每行的格式为:
ID K ID[1] ID[2] ... ID[K]
ID 是一个两位数字,表示一个非叶子结点编号,K 是一个整数,表示它的子结点数,接下来的 K 个 ID[i] 也是两位数字,表示一个子结点的编号
思路
模拟..
#include<bits/stdc++.h>
using namespace std;
const int N=105;
struct node {
vector<int> sons;
} a[N];
void bfs(int u) {
queue<int> q; q.push(u);
vector<int> v;
while (!q.empty()) {
int cnt=0;
for (int i=q.size(); i>0; i--) {
int rt=q.front(); q.pop();
if (a[rt].sons.empty()) cnt++;
for (int son : a[rt].sons) {
q.push(son);
}
}
v.push_back(cnt);
}
for (int i=0; i<v.size(); i++) {
cout<<v[i];
if (i!=v.size()-1) cout<<' ';
}
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n,m; cin>>n>>m;
for (int i=0; i<m; i++) {
int rt,k; cin>>rt>>k;
for (int j=0; j<k; j++) {
int son; cin>>son;
a[rt].sons.push_back(son);
}
}
bfs(1);
return 0;
}
Acute Stroke
现在将脑部区域看作是一个 M×N×L 的立方体,通过仪器检测,我们可以得到每个单位体积的脑部区域是否中风。
每个单位区域只与其上下左右前后六个方向直接相连的单位区域算作直接连通。
现在,给定脑部整体中风状况分析,请你计算危险中风区域的总体积,即统计所有的体积不小于 T 的连通中风区域,计算它们的体积和。
思路
这题是让你将三维的立方体存到三维数组里。略..
注:pat上的栈空间默认是1MB,所以如果用DFS实现会爆栈。
Heap Paths(30分)
给定完全二叉树的层序遍历序列。先输出右子树中的路径,再输出左子树中的路径;并判断这棵完全二叉树的堆性质
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n, a[N], b[N], isMaxHeap, isMinHeap;
void dfs(int i, int c) {
b[c]=a[i];
if (2*i>n) { //第一个儿子结点的编号越界,证明当前结点所属层是最后一层
for (int j=1; j<=c; j++) {
cout<<b[j];
if (j!=c) cout<<' ';
}
cout<<'\n';
for (int j=2; j<=c; j++) {
if (b[j-1]>b[j]) isMaxHeap=1;
else isMinHeap=1;
}
return;
}
if (2*i+1<=n) dfs(2*i+1, c+1); //先右后左
if (2*i<=n) dfs(2*i, c+1);
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
cin>>n; for (int i=1; i<=n; i++) cin>>a[i];
dfs(1,1);
if (isMaxHeap && isMinHeap) cout<<"Not Heap";
else cout<<(isMaxHeap ? "Max Heap" : "Min Heap");
return 0;
}


