b_aw_旅游计划(树的中心变形)
如果一个交叉路口位于 W 市交通网最长路径上,那么这个路口必定拥挤不堪。
所谓最长路径,定义为某条路径 p=(v1,v2,…,vk),路径经过的路口各不相同,且城市中不存在长度大于 k 的路径(因此最长路径可能不唯一)。
因此 W 市市长想知道哪些路口位于城市交通网的最长路径上。
输出
所有最长路径上的路口编号按编号顺序由小到大依次输出
方法一:树形dp求最长+次长+往上走的最长路径
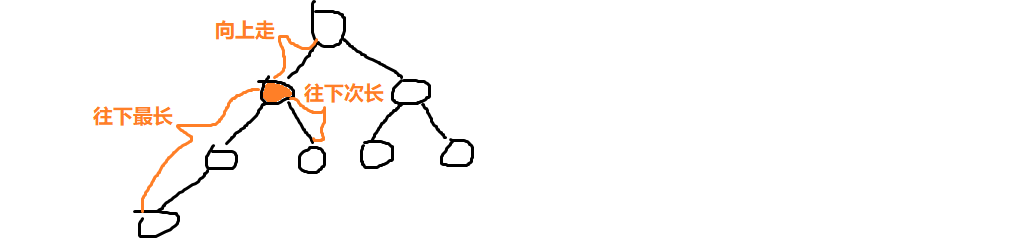
- 定义状态:
- f[i] 表示从结点i开始往下走的最长路径
- g[i] 表示从结点i开始往下走的次长路径
- h[i] 表示从结点i开始往上走的最长路径
- 思考初始化:
- f[...]=g[...]=h[i]=0
- 思考状态转移方程:
- 看代码...
- 思考输出:...
这里要注意:往上走后的下一步有两种选择:
- 继续往上走,即 h[u]=h[v]+1
- 往下走,此时又有两种情况:
- 看dfs_u中的代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
vector<int> G[N];
int f[N], g[N], h[N], son[N], maxd;
void dfs_d(int u, int fa) {
for (int v : G[u]) if (v!=fa) {
dfs_d(v, u);
if (f[v]+1>f[u]) {
g[u]=f[u], f[u]=f[v]+1;
son[u]=v;
} else if (f[v]+1>g[u]) {
g[u]=f[v]+1;
}
}
maxd=max(maxd, f[u]+g[u]);
}
void dfs_u(int u, int fa) {
for (int v : G[u]) if (v!=fa) {
h[v]=h[u]+1; //往上走
if (son[u]==v) h[v]=max(h[v], g[u]+1); //v是u的最长路径的子节点,则不能经过v,那只能和次长路相比
else h[v]=max(h[v], f[u]+1); //否则,v不是u所属最长路的结点,则可与u所属的最长路比较
dfs_u(v, u);
}
}
int main() {
std::ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin>>n;
for (int i=1; i<n; i++) {
int u,v; cin>>u>>v;
G[u].push_back(v);
G[v].push_back(u);
}
dfs_d(0,-1);//下
dfs_u(0,-1);//上
for (int i=0; i<n; i++) {
int d[3]={f[i], g[i], h[i]}; sort(d, d+3);
if (d[1]+d[2]==maxd) cout << i << '\n';
}
return 0;
}
复杂度分析
- Time:\(O(n)\),
- Space:\(O(n)\),


