关于Bell数的一道题目

 

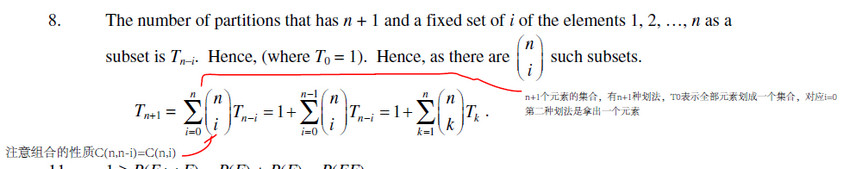
考虑 T3+1  {1,2,3,4}

T3是3个元素的划分，如果在里面加入子集{4},   4被标成特殊元素，  就形成了T4一类的划分（里面的子集的并集是{1,2,3,4})

 

T2是2个元素的划分，如果在里面加入子集{4,x1} -- x是从{1,2,3}里面任意取一个， {4,x}加到T2的划分中形成了T4的一类划分。 就是带特殊元素4,子集是2个元素的{4,x}形式的一类划分。

 

T1是1个元素的划分，如果在里面加入子集{4,x1,x2}--x1,x2是从{1,2,3}里任意取二个,{4,x1,x2}加到T1的划分中形成了T4的一类划分。就是带特殊元素4，子集是2个元素的{4,x1,x2}形式的一类划分。

 

T0是0个元素的划分，如果在里面加入子集{4,x1,x2,x3}--x1,x2,x3是从{1,2,3}里任意取3个。 {4，x1,x2,x3}加入到T0中形成T4的一类划分。 这个也就对应2.8题公式前面的数字1

 

现在讨论这个划分的合理性:

带特殊元素的子集在 n+1的情况下有 :

设第n+1个元素是sEle

1个元素（长度）{sEle}  共 C(n,0)=1种。{sEle}加入到Tn的划分中就形成了Tn+1的一类划分。

2个元素  (长度)  {sEle,1} {sEle,2} {sEle,3}.....{sEle,n} 共  C(n,1)种 。{sEle,x}加入到Tn-1 中就形成了Tn+1的一类划分。

3个元素（长度）{sEle,1,2}   {sEle,1,3} .....{sEle,1,n}..... 共C(n,2)种。

....................

n+1个元素(长度) {sEle,1,2,3....n} 共C(n,n)=1 种 。 {sEle,1,2,3...n}加入到Tn-n(即T0参考上图，就是空集) 中形成Tn+1的一类划分。

 

首先上面的划分，特殊元素组成的长度1个元素的子集与长度n+1的子集都涉及了，另外长度一样比方长度2但另外一个元素可以是1、2、3.、、、、n的情况也考虑了。

所以上面的划分考虑特殊元素的所有组合是完备的。 另外T0 到 Tn的每个划分是唯一的 ，比方T6的任意一个划分中的子集的并集都是[1,2,3,4,5,6}即6个元素，加入唯一的{sEle,x1,x2....}后

形成的Tn+1一个划分也是唯一的----意思是跟T7,Tx等不会出现重复的意思。

 

https://blog.csdn.net/MIKASA3/article/details/51283929

https://blog.csdn.net/wust_cyl/article/details/79323038