容斥恒等式

根据概率公理3，一系列事件并的概率可以看成一些列互不相容的事件概率的累加， 假设上文中的“某个结果"，是这些互不相容事件中的一个

4.4命题的左边看成是一系列互不相容事件概率的累加，这些事件就包括了”某个结果“，也就是某个结果的概率  P(某个结果) 在等号左边被累加了一次。

 

另一方面在等号右边

某个结果，包含于m个 Ei中， 假设右边有n个 Ei ,   那么   E1 E2 E3, 除非他们中都包含"某个结果"否则他们的交里面是不包括”某个结果"的，所有某个结果在这一成分里的贡献是0

也就是没有被累加， 等号右边第一组成分 累加P(Ei) 里面的系数 C(n,1) 累有C(m,1)个是带的， 第二组成分  -累加P(EiEj)的系数 C(n,2)中有C(m,2)个是带的，最后等号右边重复累加的部分就是C(m,1) -C(m,2) +C(m,3)... C(m,m)

只要证明这些系数累加是1，那么P("某个结果")在等号右边也是被累加了一次， 等式4.4才可能成立

 

 

关于符号:

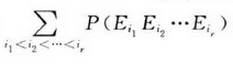
从n个元素中选择 个，并且需要满足上面的下标排列顺序

假设  n=4  ,r=3时

我们有  {1 2  3}  {1  2  4} {1  3  4}  {2  3  4}，其组数就等于C(4,3), 一般地等于C(n,r)