torch.nn.lstm参数
这里num_layers是同一个time_step的结构堆叠,Lstm堆叠层数与time step无关。Time step表示的是时间序列长度,它是由数据的inputsize决定,你输的数据时序有多长,那么神经网络会自动确定,时间序列长度只需要与你输入的数据时序长度保持一致即可。
lstm=nn.LSTM(input_size, hidden_size, num_layers)
x seq_len, batch, input_size
h0 num_layers× \times×num_directions, batch, hidden_size
c0 num_layers× \times×num_directions, batch, hidden_size
output seq_len, batch, num_directions× \times×hidden_size
hn num_layers× \times×num_directions, batch, hidden_size
cn num_layers× \times×num_directions, batch, hidden_size
举个例子:
对句子进行LSTM操作
假设有100个句子(sequence),每个句子里有7个词,batch_size=64,embedding_size=300
此时,各个参数为:
input_size=embedding_size=300
batch=batch_size=64
seq_len=7
另外设置hidden_size=100, num_layers=1
import torch
import torch.nn as nn
lstm = nn.LSTM(300, 100, 1)
x = torch.randn(7, 64, 300)
h0 = torch.randn(1, 64, 100)
c0 = torch.randn(1, 64, 100)
output, (hn, cn)=lstm(x, (h0, c0))
>>
output.shape torch.Size([7, 64, 100])
hn.shape torch.Size([1, 64, 100])
cn.shape torch.Size([1, 64, 100])
---------------------
作者:huxuedan01
来源:CSDN
原文:https://blog.csdn.net/m0_37586991/article/details/88561746
版权声明:本文为博主原创文章,转载请附上博文链接!
二、双向LSTM模型
1、双向LSTM的结构
双向LSTM(Bidirectional Long-Short Term Memorry,Bi-LSTM)不仅能利用到过去的信息,还能捕捉到后续的信息,比如在词性标注问题中,一个词的词性由上下文的词所决定,那么用双向LSTM就可以利用好上下文的信息。
双向LSTM由两个信息传递相反的LSTM循环层构成,其中第一层按时间顺序传递信息,第二层按时间逆序传递信息。
没有去找双向LSTM的图了,就看这个双向RNN的结构来学习吧,理解了双向RNN,那么把循环层的记忆细胞换成LSTM就行。
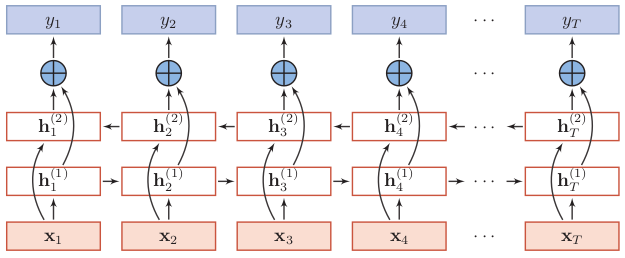
2、双向LSTM隐状态的计算
关键在于隐状态如何计算。为了简单,还是按照双向RNN的公式进行理解,我们看隐状态如何计算。可以看到t时刻第一层(顺时间循环层)的隐状态ht(1)取决于前一时刻的隐状态ht-1(1)和输入值xt,这一点非常容易理解。
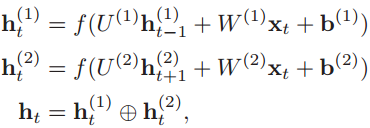
而要注意的是第二层(逆时间循环层)的隐状态则依然取决于前一时刻的隐状态和输入值x,这与堆叠的LSTM不同,堆叠的LSTM其l层的隐状态不由输入值x直接输入得到,而是取决于该层前一时刻的隐状态和当前时刻下一层的隐状态。如下的公式就是堆叠的循环网络层中隐状态的计算过程。
![]()
双向LSTM和堆叠的LSTM可以结合使用,在顺时间循环层我们可以构造堆叠多层的LSTM,同样,在逆时间循环层可以堆叠多个。
而双向LSTM的一个循环层中有两个隐状态,长期状态C用于内部传递信息,不抛头露面,而短期状态h则作为该循环层的输出,用于其他循环层或全连接层的计算。因此在对得的双向LSTM的最后一步,会有超过4个隐状态存在。
先上结论:
- output保存了最后一层,每个time step的输出h,如果是双向LSTM,每个time step的输出h = [h正向, h逆向] (同一个time step的正向和逆向的h连接起来)。
- h_n保存了每一层,最后一个time step的输出h,如果是双向LSTM,单独保存前向和后向的最后一个time step的输出h。
- c_n与h_n一致,只是它保存的是c的值。
下面单独分析三个输出:
- output是一个三维的张量,第一维表示序列长度,第二维表示一批的样本数(batch),第三维是 hidden_size(隐藏层大小) * num_directions ,这里是我遇到的第一个不理解的地方,hidden_sizes由我们自己定义,num_directions这是个什么鬼?翻看源码才明白,先贴出代码,从代码中可以发现num_directions根据是“否为双向”取值为1或2。因此,我们可以知道,output第三个维度的尺寸根据是否为双向而变化,如果不是双向,第三个维度等于我们定义的隐藏层大小;如果是双向的,第三个维度的大小等于2倍的隐藏层大小。为什么使用2倍的隐藏层大小?因为它把每个time step的前向和后向的输出连接起来了,后面会有一个实验,方便我们记忆。
2. h_n是一个三维的张量,第一维是num_layers*num_directions,num_layers是我们定义的神经网络的层数,num_directions在上面介绍过,取值为1或2,表示是否为双向LSTM。第二维表示一批的样本数量(batch)。第三维表示隐藏层的大小。第一个维度是h_n难理解的地方。首先我们定义当前的LSTM为单向LSTM,则第一维的大小是num_layers,该维度表示第n层最后一个time step的输出。如果是双向LSTM,则第一维的大小是2 * num_layers,此时,该维度依旧表示每一层最后一个time step的输出,同时前向和后向的运算时最后一个time step的输出用了一个该维度。
- 举个例子,我们定义一个num_layers=3的双向LSTM,h_n第一个维度的大小就等于 6 (2*3),h_n[0]表示第一层前向传播最后一个time
step的输出,h_n[1]表示第一层后向传播最后一个time step的输出,h_n[2]表示第二层前向传播最后一个time step的输出,h_n[3]表示第二层后向传播最后一个time step的输出,h_n[4]和h_n[5]分别表示第三层前向和后向传播时最后一个time step的输出。
3. c_n与h_n的结构一样,就不重复赘述了。
给出一个样例图(画工太差,如有错误请指正),对比前面的例子自己分析下

最后上一段代码结束战斗
import torch
import torch.nn as nn
定义一个两层双向的LSTM,input size为10,hidden size为20。
随机生成一个输入样本,sequence length为5,batch size为3,input size与定义的网络一致,为10。
手动初始化h0和c0,两个结构一致(num_layers * 2, batch, hidden_size) = (4, 3, 20)。
如果不初始化,PyTorch默认初始化为全零的张量。
bilstm = nn.LSTM(input_size=10, hidden_size=20, num_layers=2, bidirectional=True)
input = torch.randn(5, 3, 10)
h0 = torch.randn(4, 3, 20)
c0 = torch.randn(4, 3, 20)
output, (hn, cn) = bilstm(input, (h0, c0))
查看output,hn,cn的维度
print('output shape: ', output.shape)
print('hn shape: ', hn.shape)
print('cn shape: ', cn.shape)
输出:
output shape: torch.Size([5, 3, 40])
hn shape: torch.Size([4, 3, 20])
cn shape: torch.Size([4, 3, 20])
根据一开始结论,我们来验证下。
1.前向传播时,output中最后一个time step的前20个与hn最后一层前向传播的输出应该一致。
output[4, 0, :20] == hn[2, 0]
输出:
tensor([ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1], dtype=torch.uint8)
2.后向传播时,output中最后一个time step的后20个与hn最后一层后向传播的输出应该一致。
output[0, 0, 20:] == hn[3, 0]
输出:
tensor([ 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1], dtype=torch.uint8)



