贝叶斯模型,svm模型,k均值聚类,DBSCAN聚类,linux操作系统
贝叶斯模型
高斯贝叶斯分类器

实例

分析数据

计算条件概率
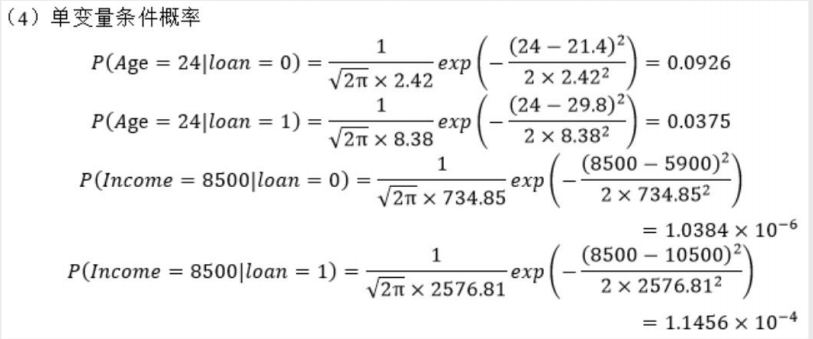
计算结果

多项式贝叶斯分类器

实例

计算因变量各类频率和单变量条件概率

获得结果

伯努利贝叶斯分类器

实例

计算因变量各类频率和单变量条件概率

获得结论

高斯贝叶斯:皮肤识别
# 读⼊数据 skin = pd.read_excel(r'C:\Users\Administrator\Desktop\Skin_Segment.xlsx') # 样本拆分 X_train,X_test,y_train,y_test = model_selection.train_test_split(skin.iloc[:,:3], skin.y, test_size = 0.25, random_state=1234) # 调⽤⾼斯朴素⻉叶斯分类器的“类” gnb = naive_bayes.GaussianNB() # 模型拟合 gnb.fit(X_train, y_train) # 模型在测试数据集上的预测 gnb_pred = gnb.predict(X_test)
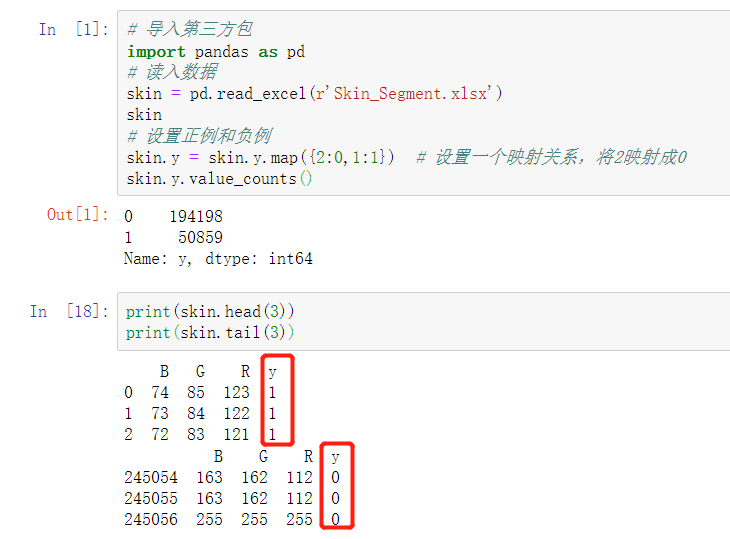
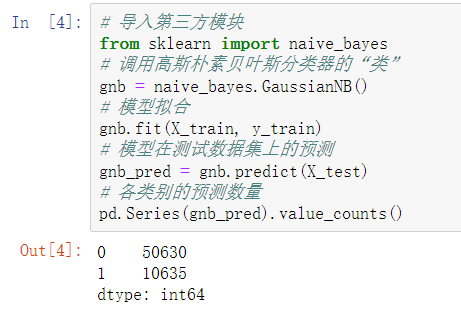
构建混淆矩阵
# 构建混淆矩阵
cm = pd.crosstab(gnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()
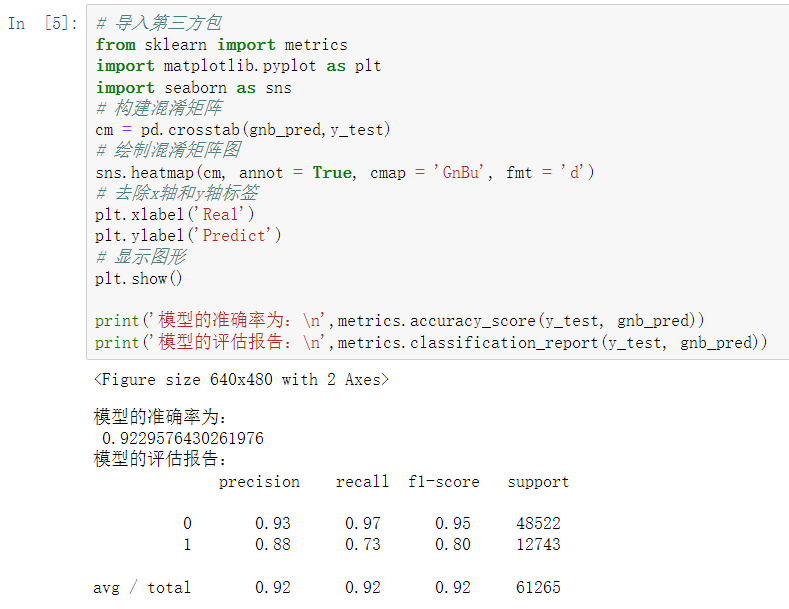
print('模型的准确率为:\n',metrics.accuracy_score(y_test,
gnb_pred))
SVM模型
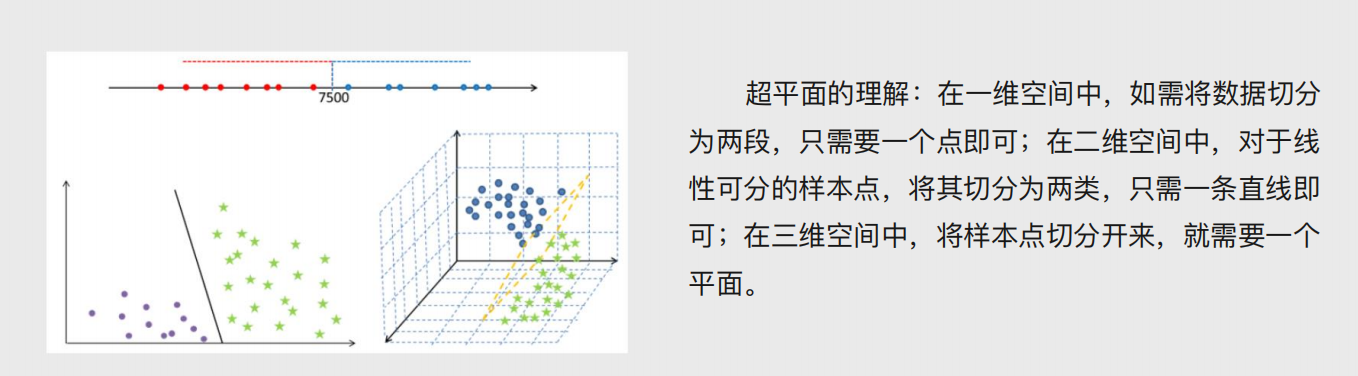
超平面的概念
将样本点划分成不同的类别(三种表现形式:点、线、面)
超平面最优解
先随机选择一条直线
分别计算两边距离改直线最短的点距离,取更小的距离
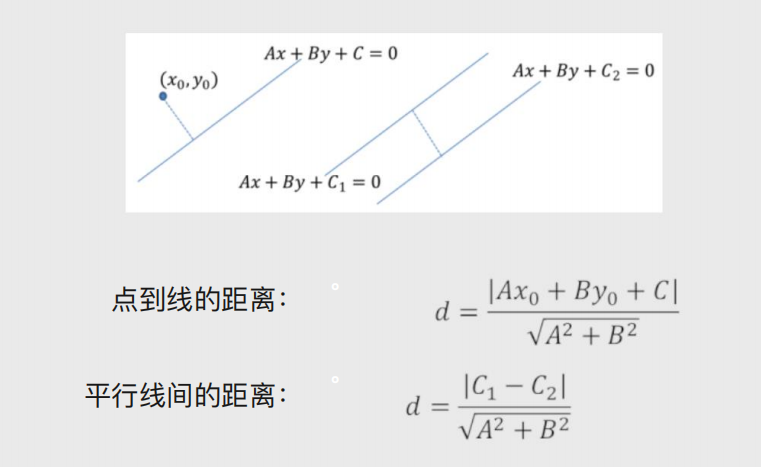
以该距离左右两边做分隔带
依次直线上述三个步骤得出N多个分隔带,最优的就是分隔带最宽的
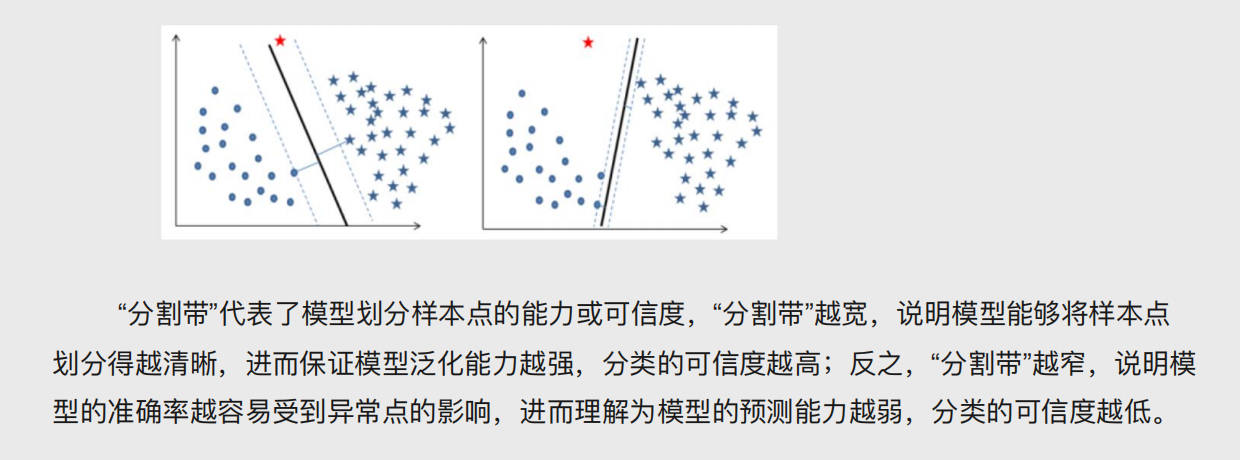
线性可分与非线性可分
线性可分:简单的理解为就是一条直线划分类别
非线性可分:一条直线无法直接划分 需要升一个维度在做划分
核函数:高斯核函数>>>:支持无穷维
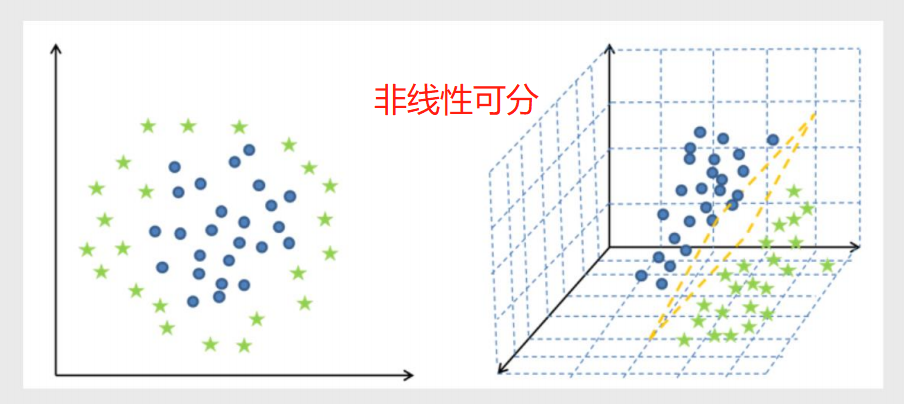
K均值聚类
K值的求解
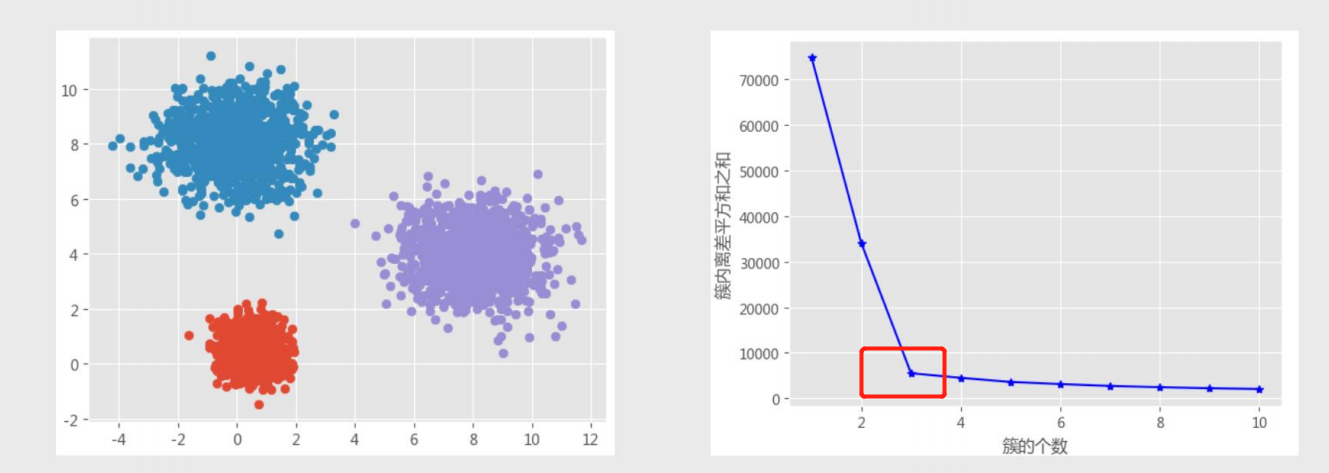
拐点法
计算不同K值下类别中离差平方和(看斜率,变化越明显越好)

代码
def k_SSE(X, clusters): # 选择连续的K种不同的值 K = range(1,clusters+1) # 构建空列表⽤于存储总的簇内离差平⽅和 TSSE = [] for k in K: # ⽤于存储各个簇内离差平⽅和 SSE = [] kmeans = KMeans(n_clusters=k) kmeans.fit(X) # 返回簇标签 labels = kmeans.labels_ # 返回簇中⼼ centers = kmeans.cluster_centers_ # 计算各簇样本的离差平⽅和,并保存到列表中 for label in set(labels): SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2)) # 计算总的簇内离差平⽅和 TSSE.append(np.sum(SSE))
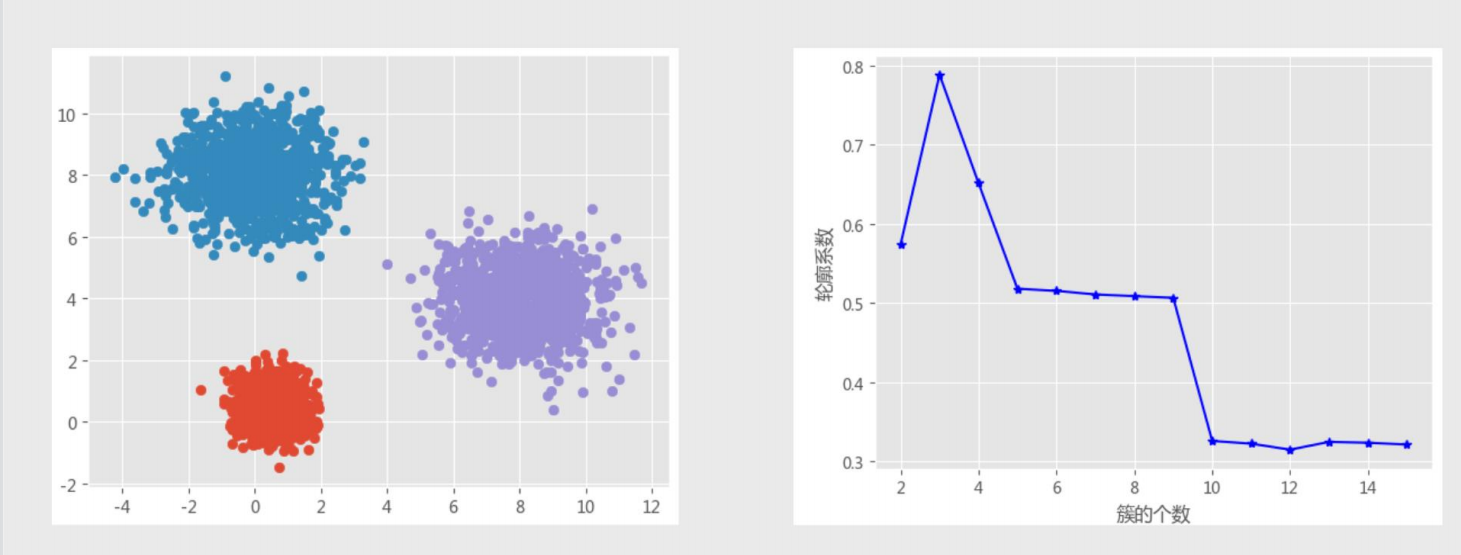
轮廓系数法

代码
# 构造⾃定义函数 def k_silhouette(X, clusters): K = range(2,clusters+1) # 构建空列表,⽤于存储不同簇数下的轮廓系数 S = [] for k in K: kmeans = KMeans(n_clusters=k) kmeans.fit(X) labels = kmeans.labels_ # 调⽤⼦模块metrics中的silhouette_score函数,计算轮廓系数 S.append(metrics.silhouette_score(X, labels, metric='euclidean'))
K均值聚类的两大缺点
聚类效果容易受到异常样本点的影响
无法准确的将非球形样本进行合理的聚类
可以采用密度聚类解决上述两个缺点
核心概念
核心对象
内部含有至少大于等于最少样本点的样本
非核心对象
内部少于最少样本点的样本
直接密度可达
在核心对象内部的样本点到核心对象的距离
密度可达
多个直接密度可达链接了多个核心对象(首尾点密度可达)
密度相连
两边的点由中间的核心对象分别密度可达
使用步骤

Kmeans聚类效果--球形簇的情况
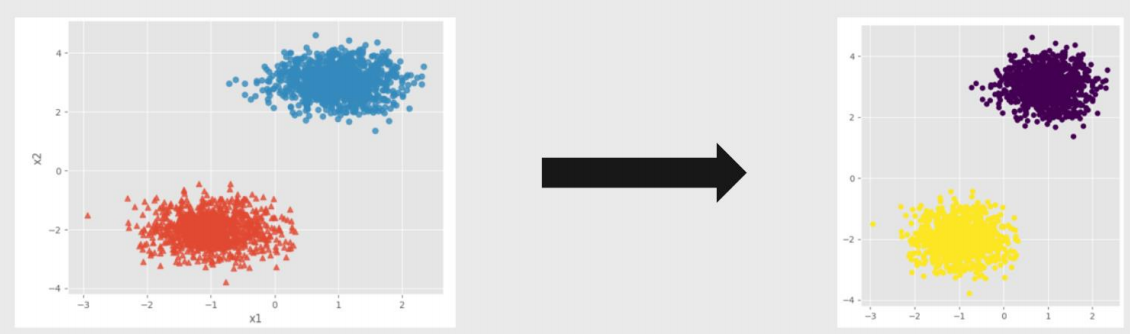
密度聚类效果--球形簇的情况
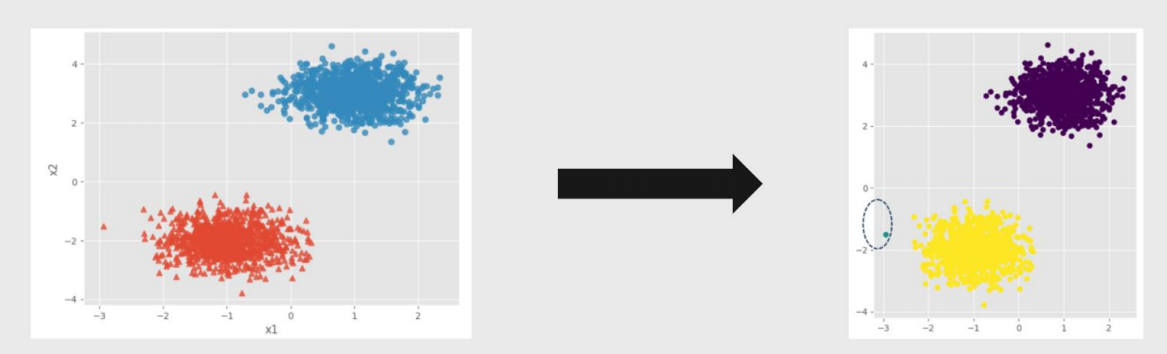
Kmeans聚类效果—⾮球形簇的情况
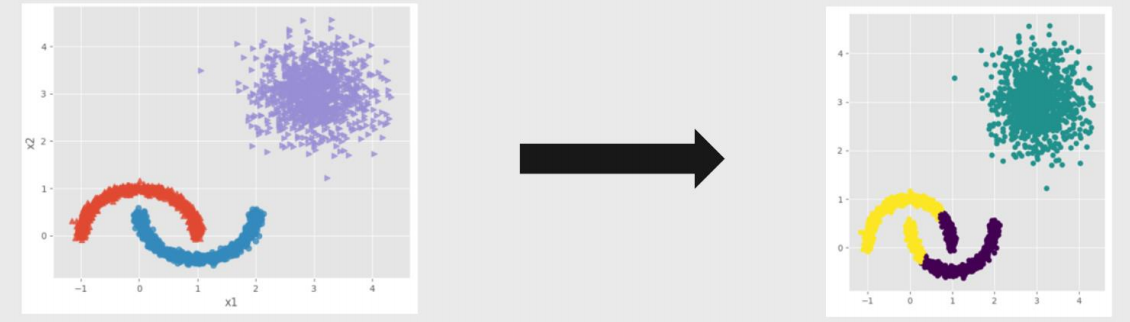
密度聚类效果—⾮球形簇的情况
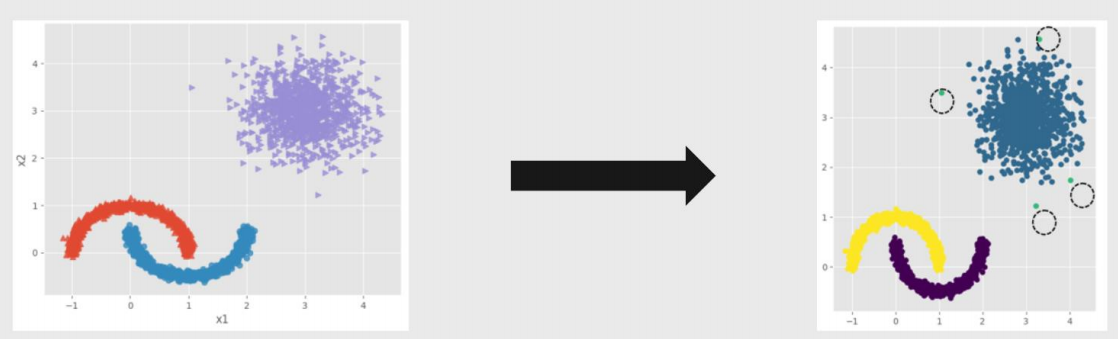
Adaboost算法
既可以解决分类问题也可以解决预测问题
由多颗基础决策树组成 并且这些决策树彼此之间有先后关系
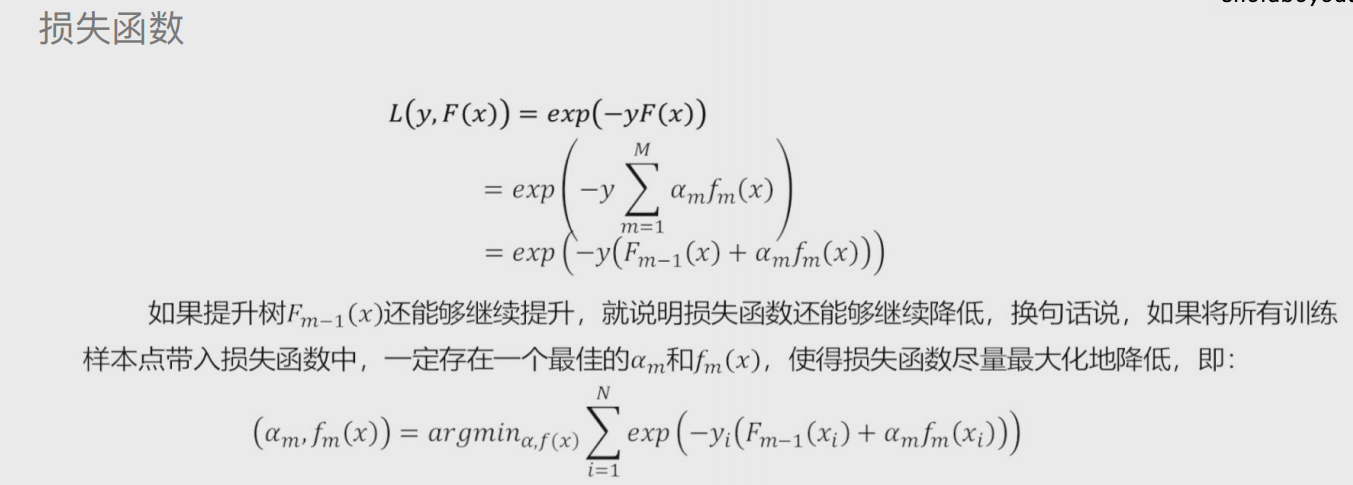
SMOTE算法
通过算法将比例较少的数据样本扩大





