线性回归模型

线性回归模型

什么是线性回归

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。

 

因变量与自变量

因变量

函数中的专业名词，也叫函数值。函数关系式中，某些特定的数会随另一个（或另几个）会变动的数的变动而变动，就称为因变量。

 

自变量

能够影响其他变量的一个变量叫做自变量，通常是x，自变量的应用范围很广，从数学、函数到计算机、编程，无处不在。

 

一元线性回归(因变量)y = a + bx(自变量)

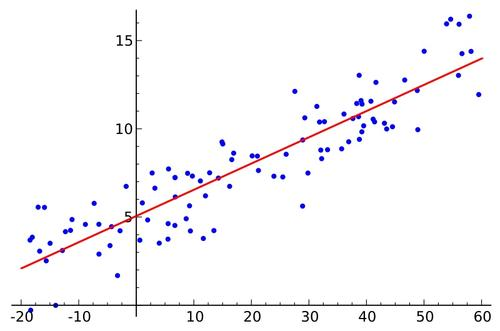
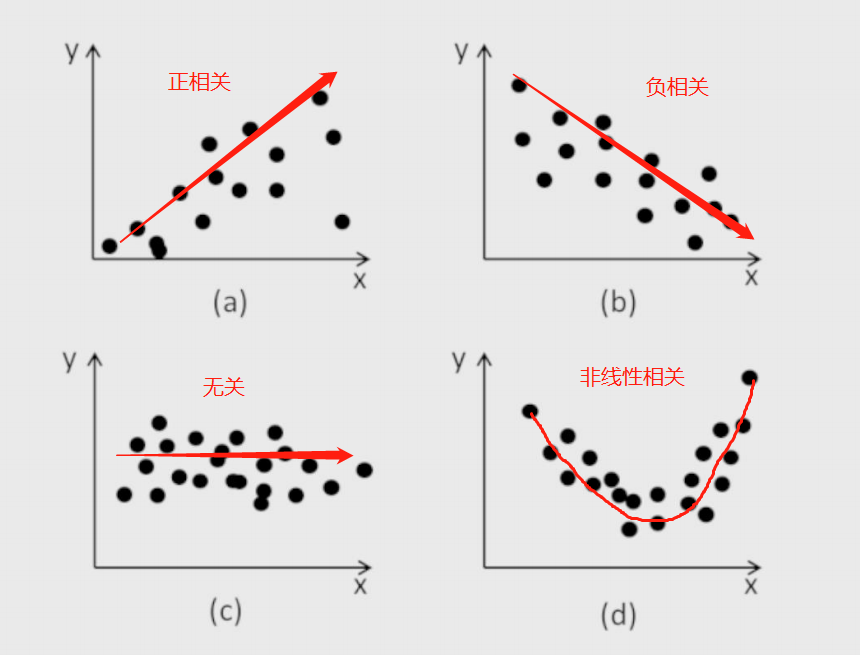
如何判断两个变量之间是否存在线性关系与非线性关系

散点图

 

公式计算

 

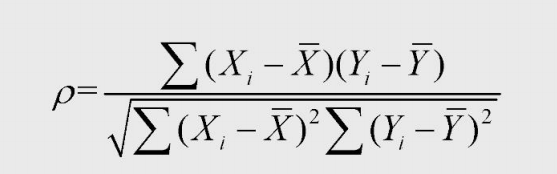
绝对值大于等于0.8表示高度相关

绝对值大于等于0.5小于等于0.8表示中度相关

绝对值大于等于0.3小于0.5表示弱相关

绝对值小于0.3表示几乎不相关

这里的不相干指的是没有线性关系，可能两者之间有其他关系

常用数学符号读法

参考网站：http://fhdq.net/sx/14.html 

 

公式计算

import numpy
import pandas
X = [52,19,7,33,2]
Y = [162,61,22,100,6]
# 1.公式计算#均值
XMean = numpy.mean(X)
YMean = numpy.mean(Y)
# 标准差
XSD = numpy.std(X)
YSD = numpy.std(Y)
# z分数
ZX = (X-XMean)/XSD
ZY = (Y-YMean)/YSD  
# 相关系数
r = numpy.sum(ZX*ZY)/(len(X))

 

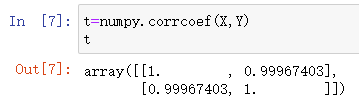
numpy中的corrcoef方法直接计算

t=numpy.corrcoef(X,Y)

 

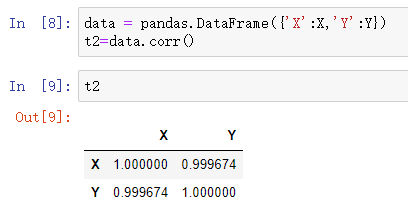
pandas中的corr方法直接计算

data = pandas.DataFrame({'X':X,'Y':Y})
t2=data.corr()

 

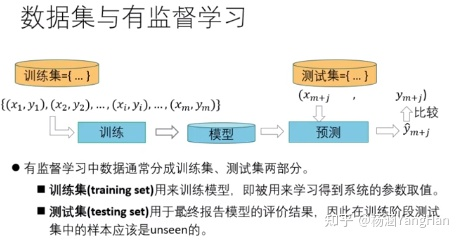
训练集与测试集

训练集用于模型的训练创建，测试集用于模型的测试检验

一般情况下训练集占总数据的80%，测试集占总数据的20%

 

哑变量

在生成算法模型的时候有些变量可能并不是数字无法代入公式计算

此时可以构造哑变量 >>> C(State)

 

自定义哑变量

生成由State变量衍生的哑变量

dummies = pd.get_dummies(Profit.State)

 

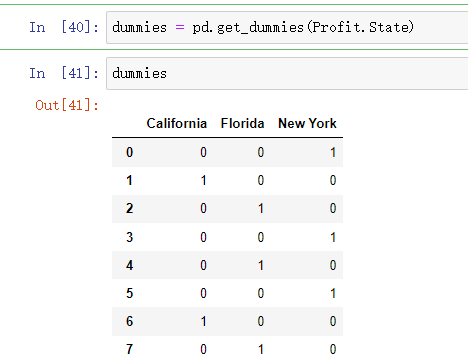
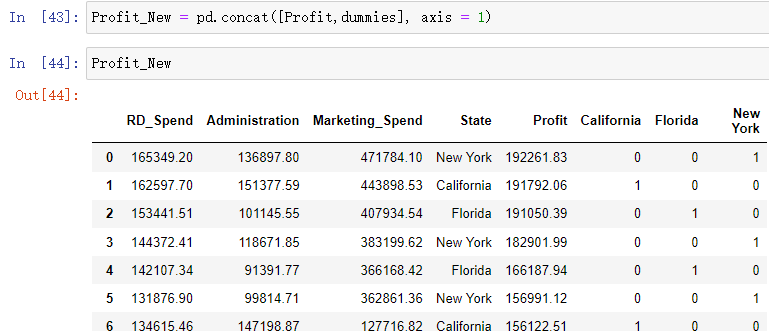
将哑变量与原始数据集水平合并

Profit_New = pd.concat([Profit,dummies], axis = 1)

 

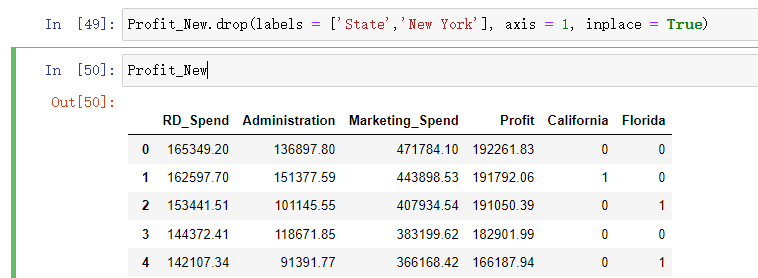
删除State变量和California变量

因为State变量已被分解为哑变量，New York变量需要作为参照组

Profit_New.drop(labels = ['State','New York'], axis = 1, inplace = True)

 

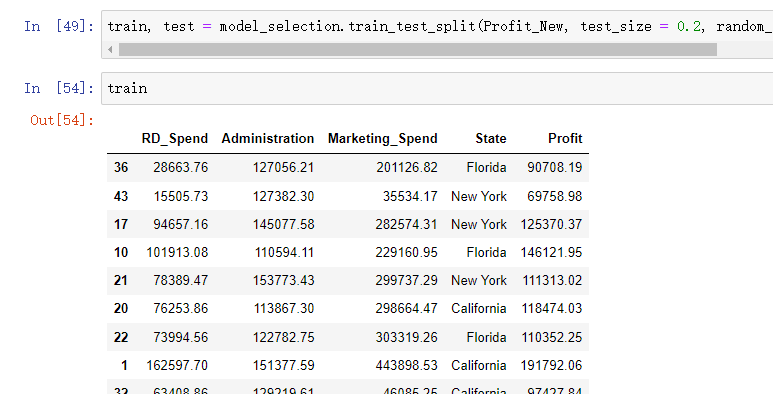
拆分数据集Profit_New

train, test = model_selection.train_test_split(Profit_New, test_size = 0.2, random_state=1234)

 

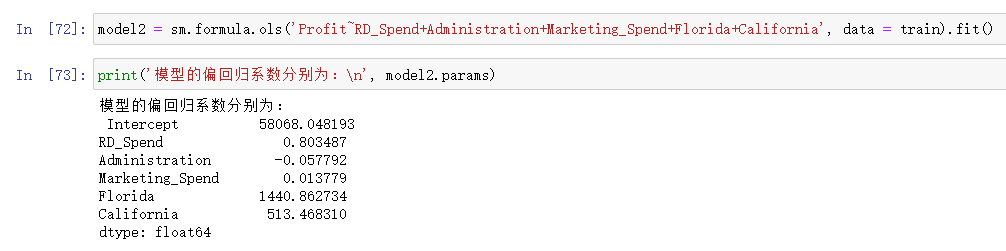
建模

model2 = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California', data = train).fit()
print('模型的偏回归系数分别为：\n', model2.params)