【语音-01】Fbank和MFCC介绍-理论和代码
【语音-01】Fbank和MFCC介绍-理论和代码
目录
- 简介
- Fbank处理过程
- MFCC
- fbank与mfcc的标准化
- fbank与mfcc的比较
一、简介
Fbank:FilterBank:人耳对声音频谱的响应是非线性的,Fbank就是一种前端处理算法,以类似于人耳的方式对音频进行处理,可以提高语音识别的性能。获得语音信号的fbank特征的一般步骤是:预加重、分帧、加窗、短时傅里叶变换(STFT)、mel滤波、去均值等。对fbank做离散余弦变换(DCT)即可获得mfcc特征。
MFCC(Mel-frequency cepstral coefficients):梅尔频率倒谱系数。梅尔频率是基于人耳听觉特性提出来的, 它与Hz频率成非线性对应关系。梅尔频率倒谱系数(MFCC)则是利用它们之间的这种关系,计算得到的Hz频谱特征。主要用于语音数据特征提取和降低运算维度。例如:对于一帧有512维(采样点)数据,经过MFCC后可以提取出最重要的40维(一般而言)数据同时也达到了降维的目的。
下面看看每个步骤的过程及知识点。
二、Fbank处理过程
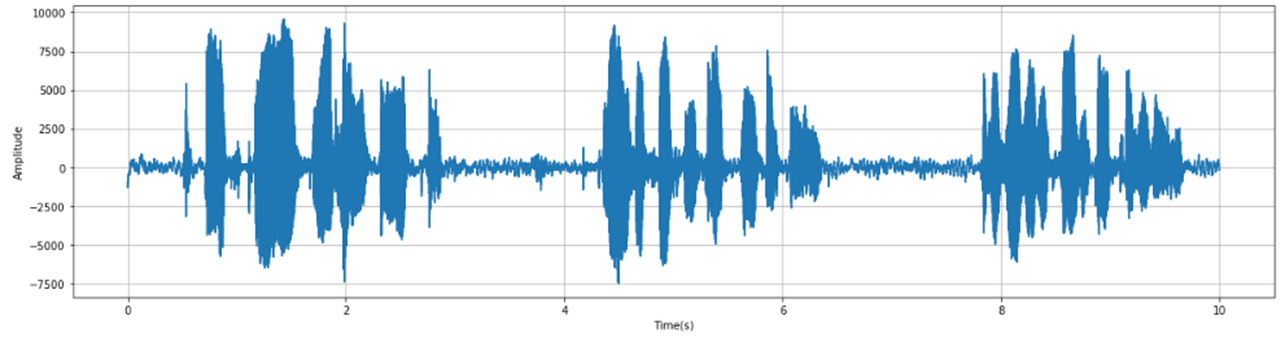
2.0 读取数据
数据下载:PCM编码的WAV格式
import matplotlib.pyplot as plt
time = np.arange(0, len(sig)) * (1.0 / fs)
def plot_freq(sig, sample_rate, nfft=512):
freqs = np.linspace(0, sample_rate/2, nfft//2 + 1)
xf = np.fft.rfft(sig, nfft) / nfft
xfp = 20 * np.log10(np.clip(np.abs(xf), 1e-20, 1e100))#强度
def plot_spectrogram(spec, ylabel = 'ylabel'):
fig = plt.figure(figsize=(20, 5))
fig.colorbar(mappable=heatmap)
wav_file = 'OSR_us_000_0010_8k.wav'
fs, sig = wavfile.read(wav_file)
#fs是wav文件的采样率,signal是wav文件的内容,filename是要读取的音频文件的路径
2.1 预处理—预加重(Pre-Emphasis)
预加重的目的:
- 平衡频谱,因为高频通常与较低频率相比具有较小的幅度,提升高频部分,使信号的频谱变得平坦,保持在低频到高频的整个频带中,能用同样的噪声比(SNR)求频谱。
- 也是为了消除发生过程中声带和嘴唇的效应,来补偿语音信号受到发音系统所抑制的高频部分,也为了突出高频的共振峰。
预加重的过程:
代码形式:emphasized_signal = numpy.append(signal[0], signal[1:] - pre_emphasis * signal[:-1])
题外话:预加重在现代系统中的影响不大,主要是因为除避免在现代FFT实现中不应成为问题的FFT数值问题,大多数预加重滤波器的动机都可以通过均值归一化来实现(在本文后面讨论)。 在现代FFT实现中。
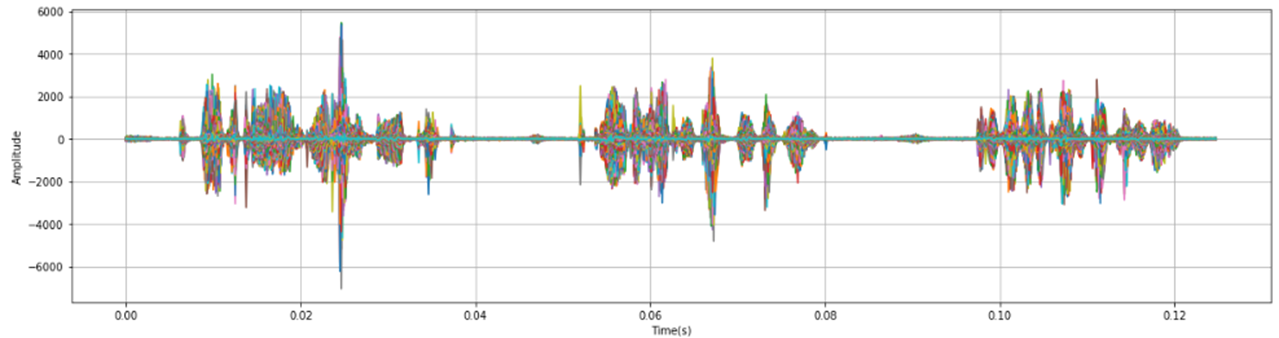
效果展示
sig = np.append(sig[0], sig[1:] - pre_emphasis * sig[:-1])
2.2 预处理—分帧(Framing)
目的:
由于语音信号是一个非平稳态过程,不能用处理平稳信号的信号处理技术对其进行分析处理。语音信号是短时平稳信号。因此我们在短时帧上进行傅里叶变换,通过连接相邻帧来获得信号频率轮廓的良好近似。
过程:
代码:
def framing(frame_len_s, frame_shift_s, fs, sig):
frame_len_n, frame_shift_n = int(round(fs * frame_len_s)), int(round(fs * frame_shift_s))
num_frame = int(np.ceil(float(sig_n - frame_len_n) / frame_shift_n) + 1)
pad_num = frame_shift_n * (num_frame - 1) + frame_len_n - sig_n # 待补0的个数
pad_zero = np.zeros(int(pad_num)) # 补0
pad_sig = np.append(sig, pad_zero)
frame_inner_index = np.arange(0, frame_len_n)
frame_index = np.arange(0, num_frame) * frame_shift_n
# 复制每个帧的内部下标,信号有多少帧,就复制多少个,在行方向上进行复制
frame_inner_index_extend = np.tile(frame_inner_index, (num_frame, 1))
frame_index_extend = np.expand_dims(frame_index, 1)
each_frame_index = frame_inner_index_extend + frame_index_extend
each_frame_index = each_frame_index.astype(np.int, copy=False)
frame_sig = pad_sig[each_frame_index]
frame_sig = framing(frame_len_s, frame_shift_s, fs, sig)
2.3 预处理—加窗(Window)
语音在长范围内是不停变动的,没有固定的特性无法做处理,所以将每一帧代入窗函数,窗外的值设定为0,其目的是消除各个帧两端可能会造成的信号不连续性。
常用的窗函数有方窗、汉明窗和汉宁窗等,根据窗函数的频域特性,常采用汉明窗。
目的:
过程:
将信号分割成帧后,我们再对每个帧乘以一个窗函数,如Hamming窗口。以增加帧左端和右端的连续性。抵消FFT假设(数据是无限的),并减少频谱泄漏。汉明窗的形式如下:
效果展示:
#frames *= numpy.hamming(frame_length)
# frames *= 0.54 - 0.46 * numpy.cos((2 * numpy.pi * n) / (frame_length - 1)) # 内部实现
window = np.hamming(int(round(frame_len_s * fs)))
plot_freq(frame_sig.reshape(-1,), fs) #需要先变成一维数据
print(frame_sig.reshape(-1,).shape)
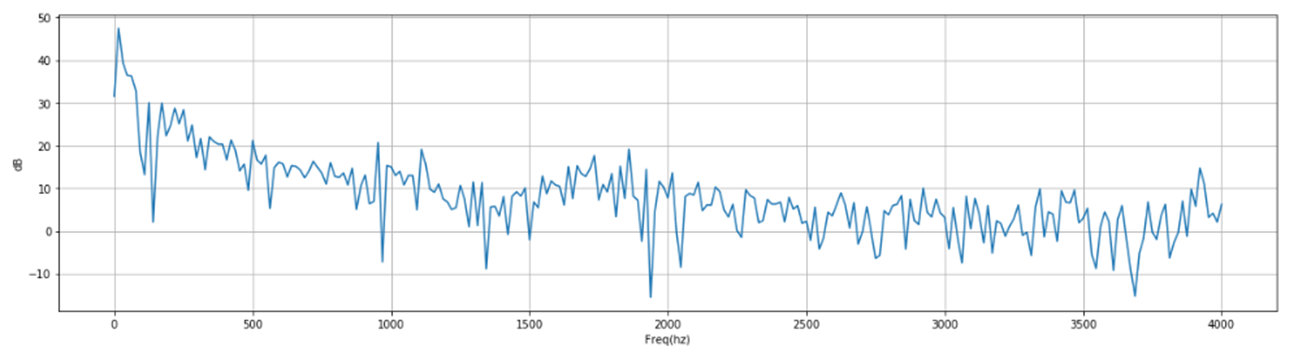
2.4 傅里叶变换FFT(Fourier-Transform)
目的
过程:
接我们对分帧加窗后的各帧信号进行做一个N点FFT来计算频谱,也称为短时傅立叶变换(STFT),其中N通常为256或512,NFFT=512;
代码:
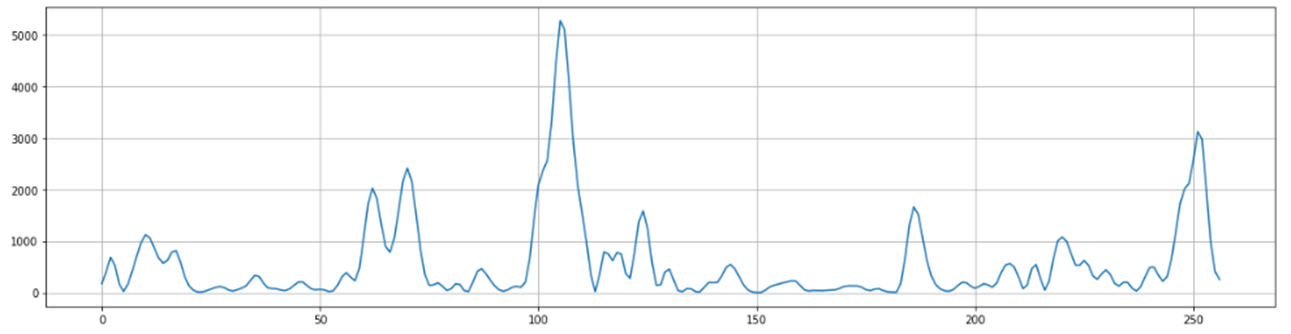
mag_frames = numpy.absolute(numpy.fft.rfft(frames, NFFT)) # fft的幅度(magnitude)
功率谱(Power Spectrum)
然后我们使用以下公式计算功率谱(周期图periodogram),对语音信号的频谱取模平方(取对数或者去平方,因为频率不可能为负,负值要舍去)得到语音信号的谱线能量。
代码和效果:
def stft(frame_sig, nfft=512):
rfft 返回 nfft // 2 + 1,即rfft仅返回有效部分
frame_spec = np.fft.rfft(frame_sig, nfft)
frame_mag = np.abs(frame_spec)
frame_pow = (frame_mag ** 2) * 1.0 / nfft
frame_pow = stft(frame_sig, nfft)
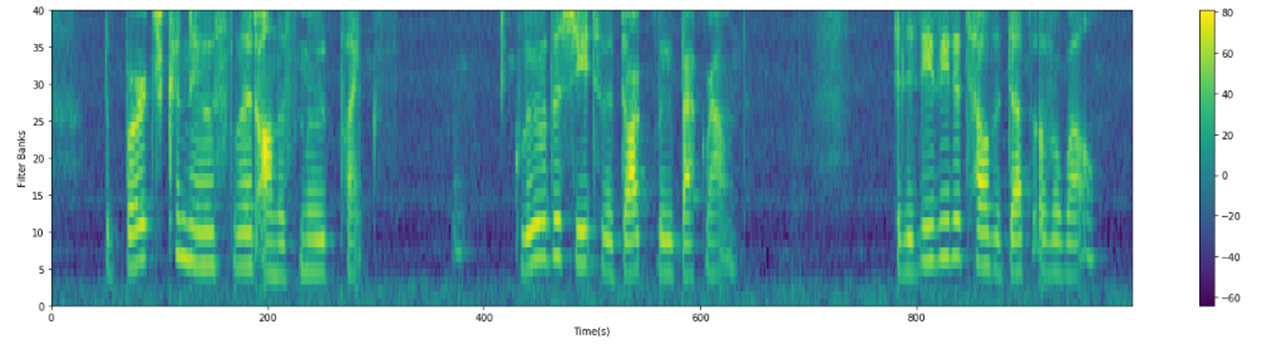
2.5 梅尔滤波器组(Filter Banks)
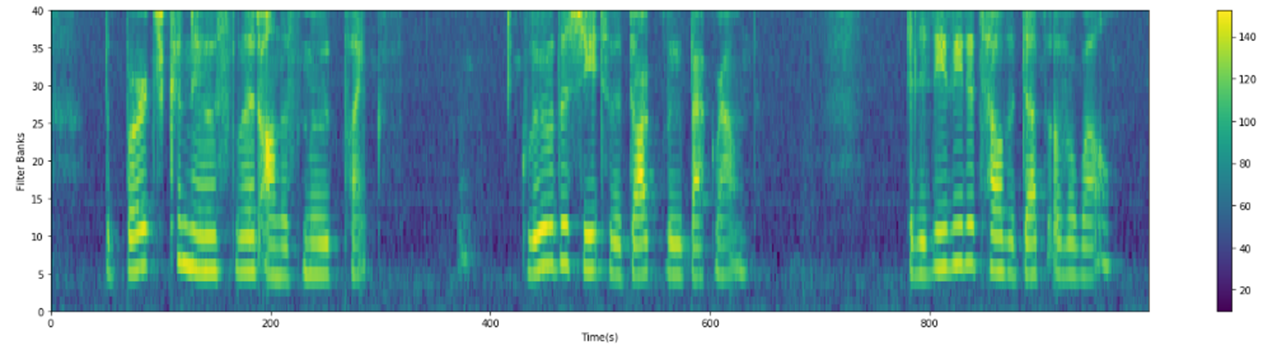
计算Mel滤波器组,将功率谱通过一组Mel刻度(通常取40个滤波器,nfilt=40)的三角滤波器(triangular filters)来提取频带(frequency bands)。
代码和效果:
def mel_filter(frame_pow, fs, n_filter, nfft):
mel = 2595 * log10(1 + f/700) # 频率到mel值映射
f = 700 * (10^(m/2595) - 1 # mel值到频率映射
mel_max = 2595 * np.log10(1 + fs / 2.0 / 700) # 最高mel值,最大信号频率为 fs/2
mel_points = np.linspace(mel_min, mel_max, n_filter + 2) # n_filter个mel值均匀分布与最低与最高mel值之间
hz_points = 700 * (10 ** (mel_points / 2595.0) - 1) # mel值对应回频率点,频率间隔指数化
filter_edge = np.floor(hz_points * (nfft + 1) / fs) # 对应到fft的点数比例上
fbank = np.zeros((n_filter, int(nfft / 2 + 1)))
for m in range(1, 1 + n_filter):
f_left = int(filter_edge[m - 1]) # 左边界点
f_center = int(filter_edge[m]) # 中心点
f_right = int(filter_edge[m + 1]) # 右边界点
for k in range(f_left, f_center):
fbank[m - 1, k] = (k - f_left) / (f_center - f_left)
for k in range(f_center, f_right):
fbank[m - 1, k] = (f_right - k) / (f_right - f_center)
# [num_frame, nfft/2 + 1] * [nfft/2 + 1, n_filter] = [num_frame, n_filter]
filter_banks = np.dot(frame_pow, fbank.T)
filter_banks = np.where(filter_banks == 0, np.finfo(float).eps, filter_banks)
filter_banks = 20 * np.log10(filter_banks) # dB
filter_banks = mel_filter(frame_pow, fs, n_filter, nfft)
plot_spectrogram(filter_banks.T, ylabel='Filter Banks')
三、MFCC
MFCC实际上就是在Fbank的基础上增加一个离散余弦变换(DCT)。
3.1 离散余弦变换(DCT)
L阶指MFCC系数阶数,通常取2-13。这里M是三角滤波器个数。
代码和效果
mfcc = dct(filter_banks, type=2, axis=1, norm='ortho')[:, 1:(num_ceps+1)] # 保持在2-13
plot_spectrogram(mfcc.T, 'MFCC Coefficients')
3.2 动态差分参数的提取
标准的倒谱参数MFCC只反映了语音参数的静态特性,语音的动态特性可以用这些静态特征的差分谱来描述。实验证明:把动、静态特征结合起来才能有效提高系统的识别性能。
式中,dt表示第t个一阶差分,Ct表示第t个倒谱系数,Q表示倒谱系数的阶数,K表示一阶导数的时间差,可取1或2。将上式的结果再代入就可以得到二阶差分的参数。
MFCC的全部组成其实是由: N维MFCC参数(N/3 MFCC系数+ N/3 一阶差分参数+ N/3 二阶差分参数)+帧能量(此项可根据需求替换)。
四、fbank与mfcc的标准化
4.1 去均值 (CMN)
filter_banks -= (np.mean(filter_banks, axis=0) + 1e-8)
plot_spectrogram(filter_banks.T, ylabel='Filter Banks')
mfcc -= (np.mean(mfcc, axis=0) + 1e-8)
plot_spectrogram(mfcc.T, 'MFCC Coefficients')
五、fbank与mfcc的比较
上述代码:https://github.com/yifanhunter/audio
参考文献
【1】 https://blog.csdn.net/fengzhonghen/article/details/51722555
【2】MFCC的理解: https://www.cnblogs.com/LXP-Never/p/10918590.html
【3】数据分析图例(代码主要来源于此):https://zhuanlan.zhihu.com/p/130926693

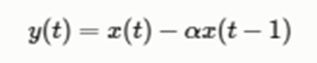

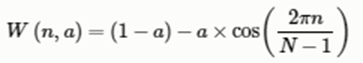


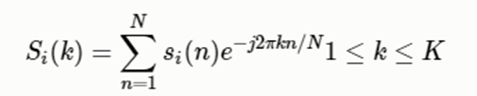

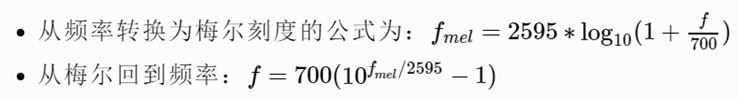

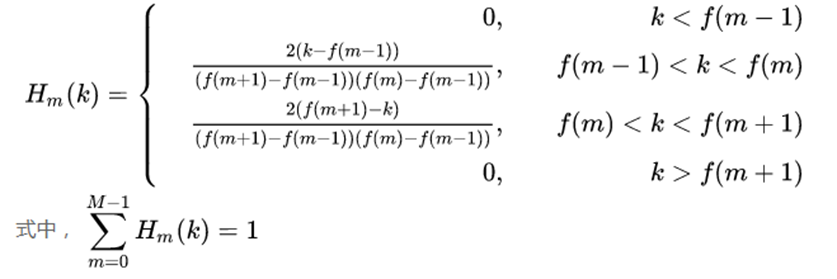
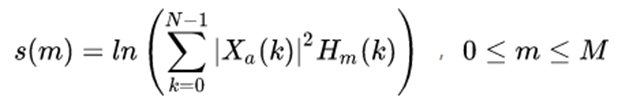
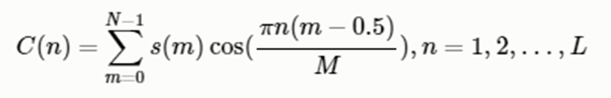

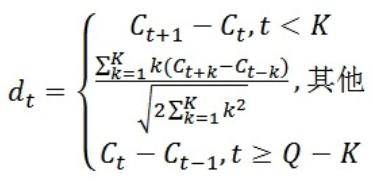


 浙公网安备 33010602011771号
浙公网安备 33010602011771号