数据结构 - 哈希表

哈希表

1. 哈希表的引入

1.1 哈希表的简单概述

　  哈希表一个通过哈希函数来计算数据存储位置的数据结构，通常支持如下操作 (高效的操作)：python中的字典是通过哈希表实现的

• insert(key, value)：插入键值对(key,value)
• get(key)：如果存在键为key的键值对则返回其value，否则返回空值
• delete(key)：删除键为key的键值对

 1.2.直接寻址表

当关键字的key 的 全域U(关键字可能出现的范围)比较小时，直接寻址是一种简单而有效的方法

       

 

• 存储 : 如上图将数组的下标作为key,将数值存储在对应的下表位置      key为k的元素放到k位置上
• 删除 : 当要删除某个元素时,将对应的下标的位置值置为空

直接寻址技术缺点：

• 当域U很大时，需要消耗大量内存，很不实际
• 如果域U很大而实际出现的key很少，则大量空间被浪费
• 无法处理关键字不是数字的情况,因为key可以是其他的数据类型

2. 哈希与哈希表

2.1 改进直接寻址表: 哈希

• 构建大小为m的寻址表T
• key为k的元素放到h(k)位置上
• h(k)是一个函数，其将域U映射到表T[0,1,...,m-1]

2.2 哈希表

 

• 哈希表（Hash Table，又称为散列表），是一种线性表的存储结构。哈希表由一个直接寻址表和一个哈希函数组成。
• 哈希函数h(k)将元素关键字k作为自变量，返回元素的存储下标。

2.2.1简单的hash函数

• 除法哈希：h(k) = k mod m
• 乘法哈希：h(k) = floor(m(kA mod 1)) 0<A<1

2.2存储机制

以除法哈希为例讨论下存储机制以及存在的问题

假设有一个长度为7的数组，哈希函数h(k)=k mod 7,元素集合{14,22,3,5}的存储方式如下图。

 解释:

• 存储 : key对数组长度取余,余数作为数组的下标,将值存储在此处
• 存在的问题 :比如：h(k)=k mod 7, h(0)=h(7)=h(14)=... 

3.哈希冲突 &解决方法

 3.1 哈希冲突

由于哈希表的大小是有限的，而要存储的值的总数量是无限的，因此对于任何哈希函数，都会出现两个不同元素映射到同一个位置上的情况，这种情况叫做哈希冲突。

3.2 解决哈希冲突

3.2.1开放寻址法

如果哈希函数返回的位置已经有值，则可以向后探查新的位置来存储这个值。

• 线性探查：如果位置i被占用，则探查i+1, i+2,……
• 二次探查：如果位置i被占用，则探查i+1^2,i+2^2……
• 二度哈希：有n个哈希函数，当使用第1个哈希函数h1发生冲突时，则尝试使用h2,h3,……

保证有空位存储  - > 动态扩张

同样装载率因子  a = n / m  a超过阈值是,将哈希表扩张一倍,重新计算哈希函数值,将值重新进行存储 

查询:线性探查的问题 : 会导致大量的空格,大量的值连在一起,导致查询的时候变慢 ,当值分散开较好

为了解决上述问题,使用二次探查的方法 

3.2.2拉链法

哈希表每个位置都连接一个链表，当冲突发生时，冲突的元素将被加到该位置链表的最后

                             

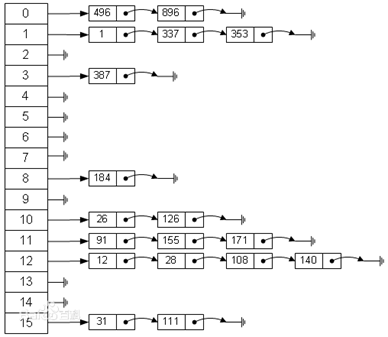
当一个位置后边的链表太长,再查找的时候会很慢

同样 拉链法也需要在装载率因子超过阈值的时候动态扩张  (但是他可以大于1)

注: 由于key必须通过hash函数计算出一个整数,因此必须是不可变的数据类型