传输线基础知识

一、传输线

1.1 传输线模型

当传输线的长度远小于电路工作时电磁波的波长时，可以将传输线的寄生参数集总在一起，用一个或有限个R、L、C元件来等效，这样的传输线系统称为集总参数电路；而当传输线的长度与工作波长可相比拟时，同一瞬间相邻两点的电压或电流不相同，这样的传输线系统称为分布参数电路。

集总参数电路和分布参数电路的分界点可认为是：

\[\frac l{\lambda}≥0.05\tag{1} \]

为了简化分析，将分布参数系统的传输线分为无限个可认为是集总参数电路的单位长度\(\Delta z\)，所以其等效电路为：

图中：
\(R\)为两段导体单位长度的电阻值，单位为Ω/m，由导体本身电导率产生。
\(L\)为两段导体单位长度的电感值，单位为H/m，由两段导体本身的自感产生。
\(G\)为两段导体单位长度的并联电导值，单位为S/m，由两导体间的电流流经介质材料所带来的损耗，称为介质损耗。
\(C\)为两段导体单位长度的并联电容值，单位为F/m，由两段导体相互靠近的电容效应产生。

1.2 传输线特性参数

在传输线方程推导与求解过程中，得到一些仅与传输线的分布参数相关的参数，被称为传输线的特性参数，详细推导过程可拜读廖承恩的《微波技术基础》。

特征阻抗\(Z_0\)

传输线的特征阻抗是指传输线上导行波的电压与电流之比：

\[Z_0=\sqrt{\frac{R+jwL}{G+jwC}}\tag{2} \]

式中：\(R\)为两段导体单位长度的电阻值；\(L\)为两段导体单位长度的电感值；\(G\)为两段导体单位长度的并联电导值；\(C\)为两段导体单位长度的并联电容值。

传播常数\(\gamma\)

传播常数是描述导行波沿导行系统传播过程中的衰减和相位变化的参数：

\[\gamma=\sqrt{\left(R+jwL\right)*\left(G+jwC\right)}=\alpha+j\beta\tag{3} \]

式中：\(\alpha\)为衰减常数，\(\beta\)为相位常数。

在无耗线\((R=G=0)\)和微波低耗线\((R\ll wL,G\ll wC)\)这两种特殊的传输线中，传输线的特征阻抗和传播常数与频率无关，仅与本身的分布参数有关。

1、无耗线
在无耗线中，\(R=G=0\)，则有：

\[Z_0=\sqrt{\frac L C}\tag{4} \]

\[\gamma=jw\sqrt{LC}\tag{5} \]

\[\alpha=0\tag{6} \]

\[\beta=w\sqrt{LC}\tag{7} \]

2、微波低耗线
在微波低耗线中，\(R\ll wL,G\ll wC\)，则有：

\[Z_0=\sqrt{\frac{R+jwL}{G+jwC}}=\sqrt{\frac{L\left(1+\frac{R}{jwL}\right)}{C\left(1+\frac{G}{jwC}\right)}}\approx\sqrt{\frac L C}\left(1+\frac R {2*jwL}\right)\left(1-\frac G {2*jwC}\right)\approx\sqrt{\frac L C}\left[1+\frac 1 2\left(\frac R {jwL}-\frac G {jwC}\right)\right]\approx\sqrt{\frac L C}\tag{8} \]

\[\gamma\approx \frac 1 2\left(R\sqrt{\frac C L}+G\sqrt{\frac L C}\right)+jw\sqrt{LC}\tag{9} \]

\[\alpha=\frac R {2*Z_0}+\frac {GZ_0} 2\tag{10} \]

\[\beta=w\sqrt{LC}\tag{11} \]

3、微带线

对于线宽为w，介质厚度为h，介电常数为\(\epsilon _r\)，导体厚度为t的微带线：

\[L(nH)\approx2*\ln\left(\frac{5.98h}{0.8w+t}\right)\tag{12} \]

\[C(pF)\approx\frac{0.264*\left(\epsilon_r+1.41\right)}{\ln\left(\frac{5.98h}{0.8w+t}\right)}\tag{13} \]

\[Z_0=\sqrt{\frac{L(H)}{C(F)}}=\sqrt{1000}\sqrt{\frac{L(nH)}{C(pF)}}\approx\frac{87}{\sqrt{\epsilon_r+1.41}}\ln{\left(\frac{5.98h}{0.8w+t}\right)}\tag{14} \]

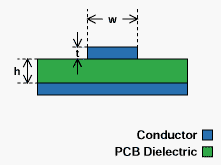
对于线宽为w，介质厚度为h，介电常数为\(\epsilon _r\)，导体厚度为t，线间距为s的微带差分线：

\[Z_{diff}\approx2Z_0\left[1-0.48e^{\frac{-0.96s}{h}}\right]\tag{15} \]

\[Z_0\approx\frac{87}{\sqrt{\epsilon_r+1.41}}\ln{\left(\frac{5.98h}{0.8w+t}\right)}\tag{16} \]

式(12)(13)(14)(15)(16)成立的条件为：

1. \(0.1<w/h<1\) 且 \(1<\epsilon _r<15\)
2. 地线宽度大于信号线宽度7倍以上；

4、带状线

对于线宽为w，介质厚度为h，介电常数为\(\epsilon _r\)，导体厚度为t的带状线：

\[Z_0\approx\frac{60}{\sqrt{\epsilon_r}}\ln{\left(\frac{4h}{0.67\pi\left(0.8w+t\right)}\right)}\tag{17} \]

对于线宽为w，介质厚度为h，介电常数为\(\epsilon _r\)，导体厚度为t，线间距为s的带状差分线：

\[Z_{diff}\approx2Z_0\left[1-0.347e^{\frac{-0.29s}{h}}\right]\tag{18} \]

\[Z_0\approx\frac{60}{\sqrt{\epsilon_r}}\ln{\left(\frac{4h}{0.67\pi\left(0.8w+t\right)}\right)}\tag{19} \]

式(17)(18)(19)成立的条件为：

1. \(w/h<0.35\) 且 \(1<\epsilon _r<15\)
2. 地线宽度大于信号线宽度7倍以上；

因此，影响传输线的特性阻抗的主要因素有：叠层材质的介电常数\(\epsilon_r\)、介质厚度h、铜的厚度t、走线的宽度w，且满足：

\[Z_0\propto\frac 1 {\sqrt{\epsilon_r}}\qquad\qquad Z_0\propto h\tag{20} \]

\[Z_0\propto\frac 1 w\qquad\qquad Z_0\propto\frac 1 t\tag{21} \]

二、地回路路径

信号在导体中传播时，会受到导体寄生参数的影响，如：电阻的衰减，电感的阻碍，给寄生电容充电和介质漏电等。

2.1 低速信号

对于低速信号而言，传输线属于集总参数电路。在信号建立过程中，信号峰头需要给寄生电容充电，同时还会通过介质漏电，所以会在信号传播路径下的参考平面上形成一个返回电流路径；直到传输线达成平衡后，不再需要给寄生电容充电，参考平面上沿传播路径的返回电流将减小(还存在介质漏电流)，其他电流将从最短路径返回。

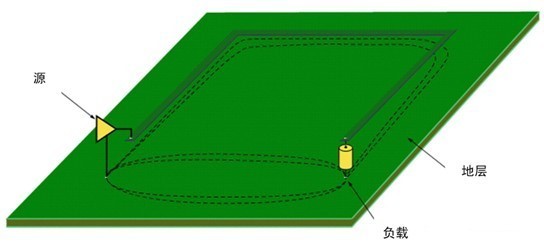
2.2 高速信号

对于高速信号而言，传输线为分布式参数电路。信号在导体中传播时，传输线上每个点的电压一直在发生变化，所以寄生电容会被反复充电和放电，绝大多数返回电流将沿信号传播路径返回。

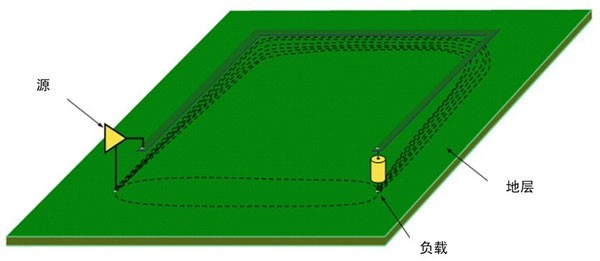
三、电信号传播速度

电信号的传播速度与导体周围介质的介电常数有关，电信号在介电常数为\(\epsilon _r\)的单一介质中传输时，其传播速度为：

\[V=\frac C{\sqrt{\epsilon _r}}\tag{22} \]

其中C为光速(\(C=3*10^8m/s\)或\(C=11.8inch/ns\))。

传输线分为微带线和带状线两种，带状线通常上下层介质的介电常数比较接近，而且有两层参考，电场和磁场会被限制在两层铜皮之间，所以式(22)比较适合带状线的电信号传输速度估算。假设FR-4板材的相对介电系数为4.7，则：

\[V=\frac {11.8}{\sqrt{4.7}}=5.44(inch/ns)\tag{23} \]

而对于微带线，我们可以用下述经验公式估算：

\[V=\frac C{B_r*\sqrt{\epsilon _r}}\tag{24} \]

\[B_r=0.8566+0.0294*\ln⁡(W)-0.00239*H-0.0101*\epsilon_r\tag{25} \]

其中\(W\)为线宽，单位为mil；\(H\)为介质厚度，单位为mil；\(\epsilon_r\)为板材的介电常数。

四、传输线延时

传输线的延时与电信号的传输速率互为倒数，所以带状线的传输线延时公式为：

\[T_p=\frac{\sqrt{\epsilon_r}}{C}=85\sqrt{\epsilon_r}(ps/inch)\tag{26} \]

微带线的传输线延时公式为：

\[T_p=\frac{B_r*\sqrt{\epsilon_r}}{C}\tag{27} \]

或

\[T_p=85\sqrt{0.475\epsilon_r+0.67}(ps/inch)=23\sqrt{\epsilon_r+1.41}(ps/cm)\tag{28} \]

式(27)(28)都是粗略估算，如果需要更精确的数据，可以用SI9000进行仿真。

特征阻抗为50Ω的微带线延时为：\(147.255(ps/inch)\)

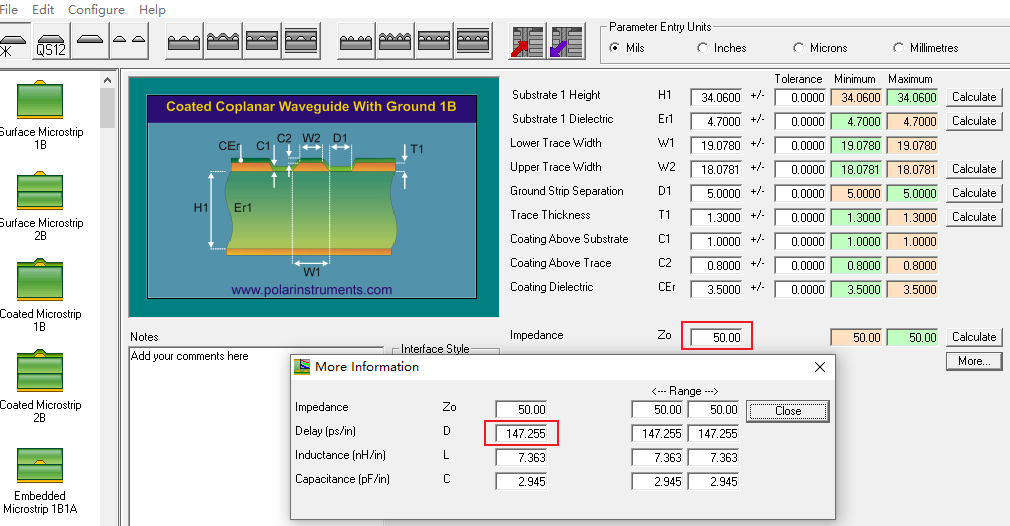
特征阻抗为50Ω的带状线延时为：\(183.68(ps/inch)\)

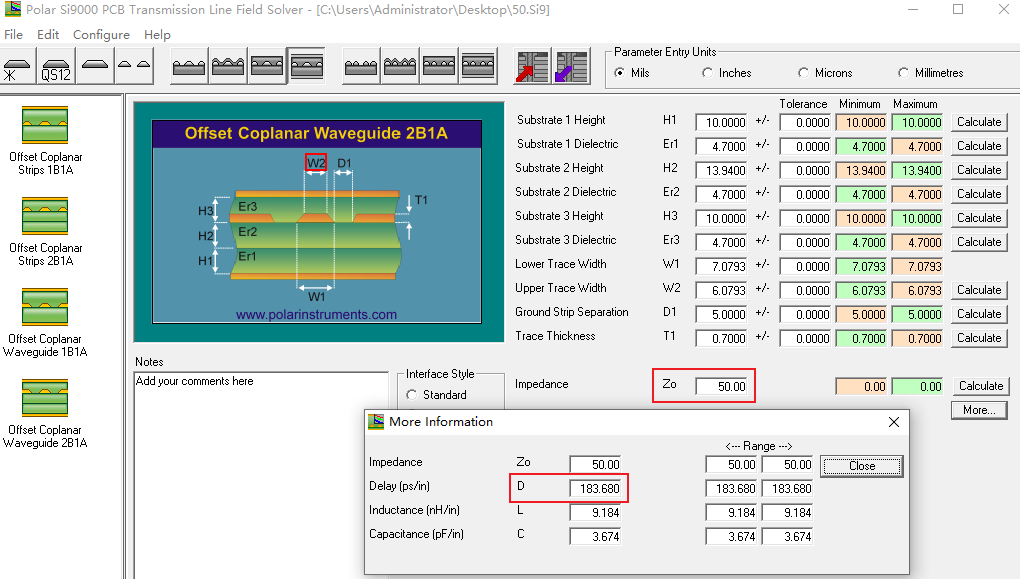
传输线延时与电信号传输速率互为倒数，所以式(18)换算成传输线延时为\(183.82(ps/inch)\)，与仿真软件计算值接近。

结合式(26)和式(27)可得：

\[\frac{T_微}{T_带}=B_r\tag{28} \]

将微带线的线宽、介质厚度和介电常数代入式(25)：\(B_r=0.8127\)

而仿真结果：\(\frac{T_微}{T_带}=\frac{147.255}{183.68}=0.8017\)

仔细观察式(25)也能发现\(B_r\)的范围将在0.8~0.85之间，所以我们可以取经验值\(B_r=0.82\)

因为传输线在微带线和带状线中的延时不同，所以高速信号的等长匹配应采用下式计算：

\[L=B_r*L_{带状线}+L_{微带线}\tag{29} \]

参考资料

1. 电路板阻抗原理知识及应用
2. 信号在传输线的传播速度到底有多快？
3. 信号在PCB上的传输时间
4. 电信号微波理论
5. 传输线理论（1）
6. 传输线及其分布电容、分布电感、特性阻抗的关系及如何计算—高速PCB设计必知必会基本知识点
7. pcb中的传输线理论