排序之选择排序

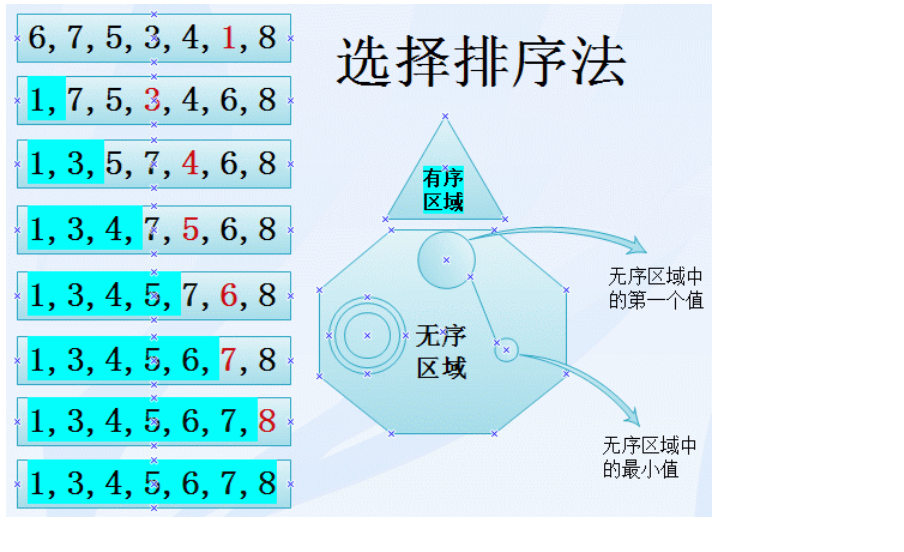
 选择排序已知一组无序数据a[1]、a[2]、……a[n]，需将其按升序排列。

首先比较a[1]与a[2]的值，若a[1]大于a[2]则交换两者的值，否则不变。
再比较a[1]与a[3]的值，若a[1]大于a[3]则交换两者的值，否则不变。
再比较a[1]与a[4]，依此类推，
最后比较a[1]与a[n]的值。
这样处理一轮后，a[1]的值一定是这组数据中最小的。

再将a[2]与a[3]~a[n]以相同方法比较一轮，则a[2]的值一定是a[2]~a[n]中最小的。

再将a[3]与a[4]~a[n]以相同方法比较一轮，依此类推。

共处理n-1轮后a[1]、a[2]、……a[n]就以升序排列了。


例如

定义数组a[]={13,4,8,2,11,67，0}

第一趟：a[]={0,4,8,2,11,67,13}

第二趟: a[]={0,2,8,4,11,67,13}

第三趟：a[]={0,2,4,8,11,67,13}

第四趟：a[]={0,2,4,8,11,67,13}

第五趟：a[]={0,2,4,8,11,67,13}

第六趟：a[]={0,2,4,8,11,13,67}

1.排序---选择排序 


选择排序的思路是：先假定一个数十最小的，后面的数与之比较，如果比它小，那么记录下标，替换最小值；依次往复，则排序完毕

选择排序的时间复杂度是o(n^2)

#include<stdio.h>
#include<stdlib.h>
#define N 100
int buffer[N];
void init_array(int a[],int n);
void print_array(int a[],int n);
void select_array(int a[],int n);

int main()
{
 init_array(buffer,N);
 printf("before sort\n");
 print_array(buffer,N);
 printf("affter sort\n");
 select_array(buffer,N);
 print_array(buffer,N); 
 
} 
void init_array(int a[],int n)
{
 int i;
 for(i=0;i<n;i++)
  a[i]=rand()%1000;  
}
void print_array(int a[],int n)
{
 int i;
 for(i=0;i<n;i++)
  printf("%d\n",a[i]); 
}
void select_array(int a[],int n)
{ int min,i,j,index;
 for(i=0;i<n-1;i++)
 {
  min=a[i];
  for(j=i+1;j<n;j++)
  {
   if(a[j]<min)
   {
    min=a[j];
    index=j;
   }
  }
  if(min!=a[i])
  {
   a[index]=a[i];
   a[i]=min;
  }
 }  
 
} 

 

 

2.选择排序原理：循环查找n个元素中最小的元素，与第一个元素进行交换；继续查找n-1个元素中最小的元素，与第二个元素交换.....直至完成

 

相比于冒泡排序算法，由于选择排序每次寻找最小元素使用的是数组下标作为标记，直到最后才进行交换移动的，所以减少了交换的次数。

需要的比较次数是固定的：n-1+n-2+n-3+…+1=n(n-1)/2次。

需要的交换次数：最好情况下为0次，最差情况下需要交换n-1次，总得时间复杂度为O(n^2)

 

 

简单选择排序
#include <iostream>
using namespace std;


//元素交换
void swap(int &a,int &b)
{
    int temp=a;
    a=b;
    b=temp;
}

/*///////////////////////////////////////////////
简单选择排序
*/
void SelectSort(int *a,int len)
{
    int i,j,pos,temp;
    for(i=0;i<len-1;i++)
    {
        pos=i;
        temp=a[i];
        for(j=i+1;j<len;j++)
        {
            if(a[j]<temp)      //若a[i]小于后面的元素，则保存较小元素的下标，
                               //并且将该元素的值保存在temp中，继续比较
            {
                pos=j;
                temp=a[j];
            }
        }
        swap(a[i],a[pos]);
    }
    for(i=0;i<len;i++)
        cout<<a[i]<<" ";
    cout<<endl;
}
/////////////////////////////////////////////////




int main()
{
    int n,i,a[20];
    cout<<"请输入数组元素n:"<<endl;
    cin>>n;
    cout<<"请输入"<<n<<"个元素:"<<endl;
    for(i=0;i<n;i++)
        cin>>a[i];
    SelectSort(a,n);
    return 0;
}

 

 3.

复杂度：O(n²)

基本思想：每一趟在n-i+1 (i=1,2,...,n-1)个记录中选取关键字最小的记录作为有序序列中的第i个记录

 

#include <stdio.h>
int SelectMinKey(int *a,int ibound)
{
    int min= a[ibound];
    for(int i=ibound+1;i<sizeof(a)/sizeof(a[0]);i++)
    {
        if(min>a[i])
            min=a[i];
    }
    return min;
}

void SelectSort(int *a, int size)
{
    int tempi;
    for(int i=1;i<size;i++)
    {
        int j = SelectMinKey(a,i);
        if(i!=j)
        {
            tempi = a[i];
            a[i]=a[j];
            a[j]=tempi;
        }
    }
}
//输出内容
void print_content(int *a, int size)
{
    for(int i=0;i<size;i++)
    {
        printf("%d\t",a[i]);
    }
    printf("\n");
}
int main(void)
{
    int a[]={0,7,8,9,3,4,5,1,2,6,11,10,13,12};
    SelectSort(a,sizeof(a)/sizeof(a[0]));//40/4
    print_content(a,sizeof(a)/sizeof(a[0]));
    return 0;
}

 

 

4，

 

 

 

 

 

5======