一个可扩展的深度学习框架的Python实现(仿keras接口)
一个可扩展的深度学习框架的Python实现(仿keras接口)
动机
keras是一种非常优秀的深度学习框架,其具有较好的易用性,可扩展性。keras的接口设计非常优雅,使用起来非常方便。在这里,我将仿照keras的接口,设计出可扩展的多层感知机模型,并在多维奇偶校验数据上进行测试。
本文实现的mlp的可扩展性在于:可以灵活指定神经网络的层数,每层神经元的个数,每层神经元的激活函数,以及指定神经网络的损失函数
本文将尽量使用numpy的矩阵运算用于训练网络,公式的推导过程可以参考此篇博客,细节上可能有所不同。
本文将只实现批量梯度下降用于训练网络,对于规模较大的数据集可扩展性不强;本文只实现了固定步长的学习率算法,将来可能会拓展到动态学习率算法;本文只实现了二分类问题的平方损失函数,对于多分类问题,用户可以自定义损失函数;
# -*- coding: utf-8 -*-
import numpy as np
from matplotlib import pyplot as plt
测试数据生成
此函数将生成n维二进制数据及其奇偶校验码
输入:
n_dim:需要生成的二进制数据的维度
输出:
X_train:n维二进制数据
y_train:以上二进制数据的奇偶校验码
#2维测试数据
#X_train=np.array([[0,0],[0,1],[1,0],[1,1]])
#y_train=np.array([0,1,1,0])
#生成用于奇偶校验的训练数据
def generate_data(n_dim):
X_train=[]
y_train=[]
for i in range(2**n_dim):
v=[0]*n_dim
x=i
for j in range(n_dim-1,-1,-1):
v[j]=x%2
x//=2
X_train.append(v)
y_train.append(sum(v)%2)
return np.array(X_train),np.array(y_train)
测试
X_train,y_train=generate_data(n_dim=3)
print(X_train)
print(y_train)
[[0 0 0]
[0 0 1]
[0 1 0]
[0 1 1]
[1 0 0]
[1 0 1]
[1 1 0]
[1 1 1]]
[0 1 1 0 1 0 0 1]
感知机模型实现
class MLP:
def __init__(self):
#使用列表保存所有的感知机层
self.layer=[]
#设置优化器
self.optimizator=None
#用于保存每一次迭代过程中的损失,最后可以用来对损失变化情况绘图
self.loss=[]
#设置损失函数
self.loss_func=None
#设置损失函数的梯度函数
self.loss_grad=None
#可以用于给mlp加一个层
def add(self,layer):
self.layer.append(layer)
#编译模型结构,初始化模型参数
def compile(self,loss='squared_loss',optimizator=None,epsilon=4):
#指定模型的优化方式,本文没有实现
self.optimizator=optimizator
#指定模型的损失函数
self.loss_func=loss_function[loss]
#设置损失函数的梯度函数
self.loss_grad=gradient_function[loss]
for i in range(len(self.layer)):
#初始化参数矩阵
if i==0:
row=self.layer[i].input_shape[0]
else:
row=self.layer[i-1].size
column=self.layer[i].size
#将参数设置为[-epsilon, epsilon]区间上均匀分布的随机数
self.layer[i].weight=np.random.rand(row,column)*2*epsilon-epsilon
self.layer[i].bias=np.random.rand(1,column)*2*epsilon-epsilon
#对模型进行拟合训练
def fit(self,X,y,epochs=10000,lr=0.01):
epoch=0
y=y.reshape((-1,1))
while epoch < epochs:
#前向传播计算每层的输出
self.__forward__(X,y)
#将此次迭代的损失保存下来
self.loss.append(self.loss_func(model.layer[-1].output,y))
#反向传播计算每层参数的变化量
self.__backward__(X,y,lr)
#更新参数
for i in range(len(self.layer)):
self.layer[i].weight+=self.layer[i].weight_change
self.layer[i].bias+=self.layer[i].bias_change
epoch+=1
#预测样本类别
def predict(self,X_test):
self.__forward__(X_test)
y_pred=self.layer[-1].output
y_pred[np.less(y_pred,0.5)]=0
y_pred[np.greater_equal(y_pred,0.5)]=1
return y_pred.astype('int').ravel()
#评估在测试集上的分类是否正确
def evaluate(self,X_test,y_test):
y_pred=self.predict(X_test)
return np.logical_not(np.logical_xor(y_pred,y_test.astype('bool')))
#评估在测试上进行分类的正确率
def evaluate_accuracy(self,X_test,y_test):
is_correct=self.evaluate(X_test,y_test)
return np.sum(is_correct)/is_correct.shape[0]
#可视化模型训练过程中的损失变化
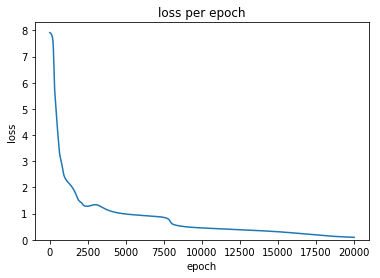
def print_loss(self):
plt.plot(self.loss)
plt.ylim(ymin=0)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('loss per epoch')
plt.show()
#前向传播过程
def __forward__(self,X,y=None):
for i in range(len(self.layer)):
#获取每一层的输入数据
if i==0:
input_data=X
else:
input_data=self.layer[i-1].output
#更新每一层的输出
self.layer[i].net=np.dot(input_data,self.layer[i].weight)+self.layer[i].bias
self.layer[i].output=self.layer[i].activation(self.layer[i].net)
#反向传播过程
def __backward__(self,X,y,lr):
for i in range(len(self.layer)-1,-1,-1):
if i==len(self.layer)-1:
temp=-1*self.loss_grad(y,self.layer[i].output)
else:
temp=np.dot(self.layer[i+1].sensitivity,np.transpose(self.layer[i+1].weight))
#计算每一层的敏感度,权重变化
self.layer[i].sensitivity=self.layer[i].gradient(self.layer[i].net)*temp
self.layer[i].weight_change=(lr)*np.dot(np.transpose(self.layer[i-1].output),self.layer[i].sensitivity)
self.layer[i].bias_change=(lr)*np.sum(self.layer[i].sensitivity,axis=0).reshape((1,-1))
感知机层类
class Layer:
def __init__(self,size,activation='sigmoid',input_shape=None):
#本层感知机的数量
self.size=size
#本层感知机的激活方式
self.activation=activation_function[activation]
#本层感知机的激活函数的求导函数
self.gradient=gradient_function[activation]
#mlp的输入维度,只对第一层的感知机有效。注意在这个模型中并没有定义输入层。
self.input_shape=input_shape
#此层感知机的输入
self.input=None
#此层感知机的权重矩阵
self.weight=None
#权重变更
self.weight_change=None
#偏置变更
self.bias_change=None
#此层感知机的偏置矩阵
self.bias=None
#记录神经元激活前的状态
self.net=None
#此层感知机的输出矩阵
self.output=None
#此层感知机的敏感度矩阵,误差逆传播的时候会用到
self.sensitivity=None
定义需要用到的损失函数和激活函数,定义其梯度函数
def squared_loss(y,y_pred):
return 0.5*np.sum(np.square(y-y_pred))
def squared_loss_gd(y,y_pred):
return y_pred-y
def sigmoid(x):
return 1/(1+np.exp(-1*x))
def sigmoid_gd(x):
return sigmoid(x)*(1-sigmoid(x))
def relu(x):
y=x
y[np.less(y,0)]=0
return y
def relu_gd(x):
g=x
g[np.less(x,0)]=0
g[np.equal(x,0)]=0.5
g[np.greater(x,0)]=1
return g
def softmax():
pass
def softmax_gd():
pass
#使用字典保存函数,可以实现使用字符串查阅所需函数
loss_function={'squared_loss':squared_loss}
activation_function={'sigmoid':sigmoid,'softmax':softmax,'relu':relu}
gradient_function={'squared_loss':squared_loss_gd,'sigmoid':sigmoid_gd,'softmax':softmax_gd,'relu':relu_gd}
测试
#指定奇偶校验数据的维度
dim=5
#生成训练数据
X_train,y_train=generate_data(n_dim=dim)
#设置模型参数
model=MLP()
model.add(Layer(20,'sigmoid',input_shape=(dim,)))
model.add(Layer(10,'sigmoid'))
model.add(Layer(5,'sigmoid'))
model.add(Layer(1,'sigmoid'))
model.compile(loss='squared_loss')
model.fit(X_train,y_train,epochs=20000,lr=0.01)
#输出测试结果
print('-'*100)
print('accuracy:')
print(model.evaluate_accuracy(X_train,y_train))
model.print_loss()
----------------------------------------------------------------------------------------------
accuracy:
1.0


 浙公网安备 33010602011771号
浙公网安备 33010602011771号