Perl寻路A*算法实现
A*算法;A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法。估价值与实际值越接近,估价函数取得就越好。
公式表示为: f(n)=g(n)+h(n),其中 f(n) 是从初始点经由节点n到目标点的估价函数,g(n) 是在状态空间中从初始节点到n节点的实际代价,h(n) 是从n到目标节点最佳路径的估计代价。
保证找到最短路径(最优解的)条件,关键在于估价函数f(n)的选取:估价值h(n)<= n到目标节点的距离实际值,这种情况下,搜索的点数多,搜索范围大,效率低。但能得到最优解。并且如果h(n)=d(n),即距离估计h(n)等于最短距离,那么搜索将严格沿着最短路径进行, 此时的搜索效率是最高的。如果 估价值>实际值,搜索的点数少,搜索范围小,效率高,但不能保证得到最优解。
创建两个表,OPEN表保存所有已生成而未考察的节点,CLOSED表中记录已访问过的节点。算起点的估价值;将起点放入OPEN表;保存路径,即从终点开始,每个节点沿着父节点移动直至起点,这就是你的路径。
算法伪码:
while(OPEN!=NULL) { 从OPEN表中取估价值f(n)最小的节点n; if(n节点==目标节点) break; for(当前节点n的每个子节点X) { 算X的估价值; if(XinOPEN) if(X的估价值小于OPEN表的估价值) { 把n设置为X的父亲; 更新OPEN表中的估价值;//取最小路径的估价值 } if(XinCLOSE) continue; if(Xnotinboth) { 把n设置为X的父亲; 求X的估价值; 并将X插入OPEN表中;//还没有排序 } }//endfor 将n节点插入CLOSE表中; 按照估价值将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小,从最小路径的节点向下进行。 }//endwhile(OPEN!=NULL)
以上摘自百度百科,以下将用Perl语言实现:
1、建立路径数组,下标即是步数,并使用匿名哈希保存坐标点、开销、到目的地开销、实际开销、父节点等信息,数据结构如下:
path[step]={ coordinate=>[y,x],
cost=>0,
next_cost=>(y-end.y)+(x-end.x),
previous=>path[step-1],
actual_cost=>cost+next_cost }
2、另一个数组,下标即是坐标点,指向的匿名哈希存放OPEN、CLOSE、前一节点的状态,如: arr[y][x]->{point},方便回退时能直接获取到上一步的坐标点和状态,数据结构如下:
arr[y][x]={ flag=>0,
point=>arr[y-1][x-1] }
数据结构设计好后,根据上面的伪代码实现还是比较容易:
use strict; use List::Util; use constant {WIDTH=>12,HEIGHT=>8,DEBUG=>1,}; my @uldr=( 0,[-1,0],[0,-1],[1,0],[0,1], ); # 上、左、下、右 my @bg=(); for(my $y=0;$y<HEIGHT;$y++){ for( my $x=0 ; $x<WIDTH ; $x++ ){ if( $y == 0 || $y == HEIGHT-1 || $x == 0 || $x == WIDTH-1 ){ $bg[$y][$x] = '*'; } else{ $bg[$y][$x] = ' '; } } } # 初始化迷宫 my @obstruction=( [1,5],[1,4],[1,3],[2,3],[2,5],[2,6],[3,6],[4,6],[5,6],[3,3],[3,2],[3,1], ); # 障碍物坐标 map{ $bg[ $obstruction[$_][0] ][ $obstruction[$_][1] ] = '#' } 1..$#obstruction-1; $bg[ $obstruction[0][0] ][ $obstruction[0][1] ] = '@'; @bg=( ['*','*','*','*','*','*','*','*','*','*','*','*',], ['*',' ',' ',' ','#',' ',' ',' ',' ',' ',' ','*',], ['*',' ','#',' ',' ',' ',' ',' ',' ',' ',' ','*',], ['*',' ','#',' ',' ',' ','#',' ',' ',' ',' ','*',], ['*',' ','#',' ',' ',' ','#','#','#','#','#','*',], ['*',' ',' ','#',' ',' ','#',' ',' ',' ',' ','*',], ['*',' ',' ',' ',' ',' ',' ',' ',' ',' ',' ','*',], ['*','*','*','*','*','*','*','*','*','*','*','*',], ); print @$_,"\n" foreach(@bg); my @bg_ghost=(); # 0--未经过 1--已走 2--不可通过 print "-"x15,"\n"; sub caclulate_cost{ my ($sp,$ep)=@_; return abs($sp->[0] - $ep->[0]) + abs($sp->[1] - $ep->[1]); } sub handle{ my @path=(); # 存放步数的数组 my $start=[ $obstruction[0][0] , $obstruction[0][1] ]; # 起点 $start=[1,10]; my $end=[ $obstruction[-1][0] , $obstruction[-1][1] ]; # 终点 $end=[6,9]; my ($step,$p_step,$p_gh)=(0,'',''); # 步数、指向数组元素的指针、指向bg_ghost元素的指针 $path[$step]={ coordinate=>[$start->[0],$start->[1]], cost=>0, next_cost=>&caclulate_cost( $start,$end ), previous=>0, }; # 每一步保存坐标、预计开销、到目的地距离、父节点,起点开销为0 $path[$step]->{actual_cost}=$path[$step]->{cost} + $path[$step]->{next_cost}; # 实际开销 $bg_ghost[ $start->[0] ][ $start->[1] ]->{point}=''; # 起点的父节点为空 while(@path){ $p_step=pop(@path); print " step:$step,p_step:$p_step\n" if DEBUG; if( $p_step->{coordinate}->[0] == $end->[0] && $p_step->{coordinate}->[1] == $end->[1] ){ # 到达目的地 my @arr=('A'..'Z','a'..'z'); my @temp=(); while($p_step){ push @temp,$p_step->{coordinate}; $p_step=$p_step->{previous}; # 顺着父节点回溯,获取每个节点 } @temp=reverse(@temp); foreach(0..$#temp){ $bg[ $temp[$_]->[0] ][ $temp[$_]->[1] ] = $arr[$_]; } return 1; } # end if $step++; for(my $cnt=1;$cnt<=4;$cnt++){ my $y= $p_step->{coordinate}->[0]+$uldr[$cnt][0] ; my $x= $p_step->{coordinate}->[1]+$uldr[$cnt][1] ; print " ($p_step->{coordinate}->[0],$p_step->{coordinate}->[1])+($uldr[$cnt][0],$uldr[$cnt][1]),(y,x)=($y,$x)\n" if DEBUG; if( $y < 1 || $y > HEIGHT-2 || $x < 1 || $x > WIDTH-2 || $bg[$y][$x] eq '#' ){ $bg_ghost[$y][$x]->{flag} = 2 ; # 不可经过 } if( ! $bg_ghost[$y][$x]->{flag} ){ # 未经过的 $bg_ghost[$y][$x]->{flag}=1; # 设置已经过 $bg_ghost[$y][$x]->{point}=$p_step; # 保存前一节点状态 my $px={ coordinate=>[$y,$x], cost=>$p_step->{cost}+1, next_cost=>&caclulate_cost( [$y,$x],$end ), previous=>$p_step, }; $px->{actual_cost}=$px->{cost} + $px->{next_cost}; push @path,$px; } else{ $p_gh=$bg_ghost[$y][$x]->{point}; print " p_gh:$p_gh\n" if DEBUG; if($p_gh && $p_step->{cost}+1 < $p_gh->{cost} ){ # 如果当前开销较小 print " $p_step->{cost},$p_gh->{cost}\n" if DEBUG; $p_gh->{cost}=$p_step->{cost}+1; # $p_gh->{previous}=$p_step; # 将前一个节点设置为当前节点之父 $p_gh->{actual_cost}=$p_gh->{cost}+$p_gh->{next_cost}; # 更新前一节点开销 } } } $bg_ghost[ $p_step->{coordinate}->[0] ][ $p_step->{coordinate}->[1] ]->{flag}=1; # 设置已经过 @path=sort{$b->{actual_cost}<=>$a->{actual_cost}}@path; # 排序,开销最小的放在最后 } return 0; } &handle; print @$_,"\n" foreach(@bg);
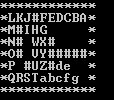
计算出来的最短路径:

比较一下深度优先算法: