视图矩阵ViewMatrix一些概念
讨论下View矩阵
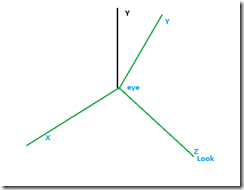
图1
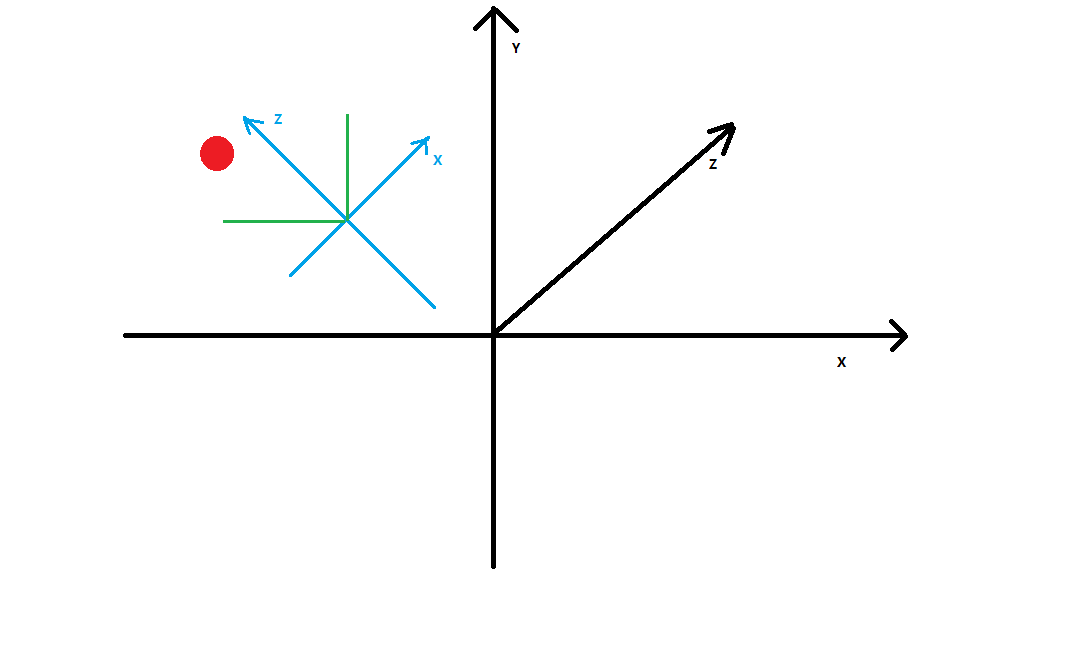
上图黑色是我们世界坐标系,浅蓝色是摄像机坐标系。
视图矩阵作用一句话简明表达就是世界坐标系转换到摄像机坐标系。
从图1 黑色的世界坐标系转换到浅蓝色的摄像机坐标系。
先说概念,我们根据摄像机的位置和旋转信息可以构造出摄像机的坐标系矩阵C,但是这个C
你单纯的乘上世界矩阵,是错误的。因为你的变化还是在世界坐标系做平移和旋转。
我们要的目的是把世界坐标系的东西变换到Camera的坐标系。以Camera中心点做世界的原点,Camera的基向量做世界坐标系的轴。
那么于“原来的世界坐标系”的向量,都得除去“现在世界坐标”基向量的影响。
公式2:
矩阵乘上他的逆矩阵得到单位矩阵。那么我们对"原来世界坐标系"的向量乘上"现在世界坐标系"矩阵的逆矩阵。
我们分解逆矩阵 
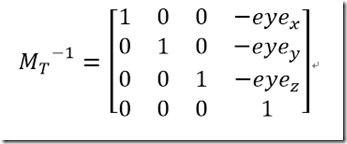
他位移部分Mt矩阵,他的平移矩阵位置。
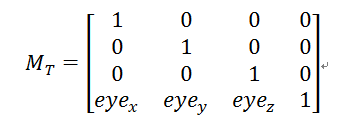
他的位移矩阵的逆矩阵就是反向位移矩阵,那么我们可以构造下面逆矩阵
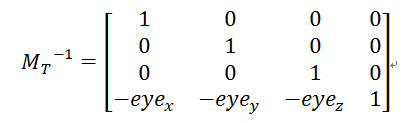
现在构造旋转部分的逆矩阵,我们知道。旋转矩阵是个正交矩阵,它的逆矩阵和转置矩阵一样得到下面。
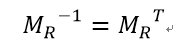
那么构造出本身的旋转矩阵,转置就得到他的逆矩阵
矩阵旋转构造,只要知道三个基向量就可以构造。
我们先用世界坐标系”Y轴基向量”,通过 look和eye点 得到Z轴基向量。
叉乘得X轴基向量,但是我们知道Y基向量,不是真正的基向量。重新叉乘得到真正的Y轴基向量。

有了三个坐标系基向量,构造旋转矩阵。
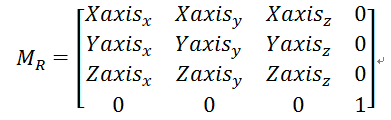
转置下
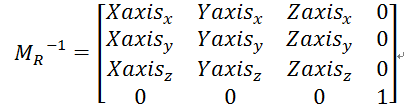
相乘就得到我们真正想要Camera矩阵
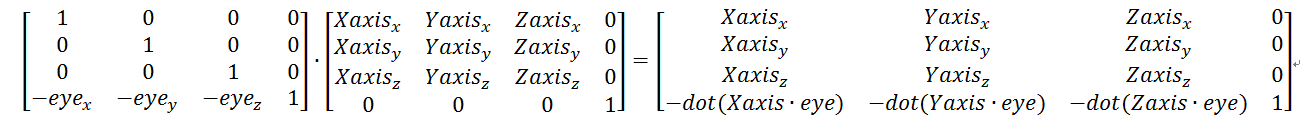
这个推导的矩阵是 左手系行向量的情况下视图矩阵(DX情况下)
下步推导下右手系列向量情况下的矩阵
平移矩阵
平移逆矩阵
旋转矩阵
逆矩阵
矩阵相乘不满足交换律,所以列向量都是右乘
到目前,左右手系视图矩阵推导完成。如果有错误谢谢指出。


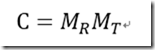





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步