猴子排序的期望复杂度推导(雾)

　　众所周知，猴子排序打破了排序算法$O(n\log{n})$的桎梏(雾)，具体的话，显然最好情况一次成功就是$O(n)$，最坏情况那就$O(+\infty)$了。期望是多少呢？让我来推导一番(逃)。

　　首先，设序列长度为$n$，每次打乱序列和检测是否有序为$O(n)$，每次成功的概率为$\frac{1}{n!}$(全排列共$n!$种)，失败的概率为$1-\frac{1}{n!}$。我们令$X$为排序成功所需的打乱次数，则$P(X=k)=P_{成功}^{1}×P_{失败}^{k-1}$(乘法原理)。那么猴子排序的期望复杂度就是$O(E(X)*n)$

　　X分布列如下表所示——

$X$	$1$	$2$	$3$	$\cdots$	$k$	$\cdots$	$+\infty$
$P(X=k)$	$\frac{1}{n!}$	$\left(1-\frac{1}{n!}\right)^{2-1}×\frac{1}{n!}$	$\left(1-\frac{1}{n!}\right)^{3-1}×\frac{1}{n!}$	$\cdots$	$\left(1-\frac{1}{n!}\right)^{k-1}×\frac{1}{n!}$	$\cdots$	$+\infty$

　　有了分布列就来求X的期望吧——

$$E(X)=1×\frac{1}{n!}+2×\left(1-\frac{1}{n!}\right)^{2-1}×\frac{1}{n!}+3×\left(1-\frac{1}{n!}\right)^{3-1}×\frac{1}{n!}+\cdots+k×\left(1-\frac{1}{n!}\right)^{k-1}×\frac{1}{n!}+\cdots$$

$$=\frac{1}{n!}×\left[1×\left(1-\frac{1}{n!}\right)^{0}+2×\left(1-\frac{1}{n!}\right)^{1}+3×\left(1-\frac{1}{n!}\right)^{2}+\cdots+k×\left(1-\frac{1}{n!}\right)^{k-1}+\cdots\right]$$

$$=\frac{1}{n!}×\sum_{i=1}^{\infty}\left[{i×\left(1-\frac{1}{n!}\right)^{i-1}}\right]$$

　　嗯……这个级数怎么求和啊？

　　写个程序跑一下吧，求和求到二百万应该够了，再往上long double的精度也不资磁了……

#include<stdio.h>
#include<math.h>
int main()
{
    double fac=1;//n!
    for(int n=1;n<=10;n++)
    {
        long double E=0;
        fac*=n;
        for(int i=1;i<=2000000;i++)
        {
            E+=i*pow((fac-1.0)/fac,i-1);
        }
        E/=fac;
        printf("E(X)=%Lf    (n=%d)\n",E,n);        
    }
    return 0;
}

 

　　运行结果——

 

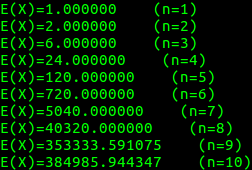
　　n大于8以后，long double都爆了……忽略它们！(观众：你……)

　　于是我们猜想——$E(X)=n!$。

　　上网一查，猴子排序复杂度果然是$O(n×n!)$，于是，猜想成立，推导完毕……（博主已被打死）

 　　

　　留坑，等我会求那坨级数求和再来填坑吧（逃）大家别学我

2019年1月21日13:45:56更新

　　填坑啦！填坑啦！（这学期高数应该不会挂了嘻嘻）

　　那个$E(X)=\frac{1}{n!}×\sum_{i=1}^{\infty}\left[{i×\left(1-\frac{1}{n!}\right)^{i-1}}\right]$是一个以$n$为自变量的幂级数，对$E(X)$逐项积分可得$$\int {E(X)\,dn}=\frac{1}{n!}×\sum_{i=1}^{\infty}\left(1-\frac{1}{n!}\right)^i$$

　　又

$$\sum_{i=1}^{\infty}k^i=\frac{1}{1-k}-1       (-1<k<1)$$

　　令$k=1-\frac{1}{n!}$

　　则$$\int {E(X)\,dn}=\frac{1}{n!}×(n!-1)=1-\frac{1}{n!}$$

　　两边再求导可得……可得啥来着？稍等……再次留坑