洛谷 P2827 BZOJ 4721 UOJ #264 蚯蚓

题目描述

本题中，我们将用符号表示对c向下取整，例如：。

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有n只蚯蚓（n为正整数)。每只蚯蚓拥有长度，我们设第i只蚯蚓的长度为，并保证所有的长度都是非负整数（即:可能存在长度为0的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0<p<1的有理数)决定，设这只蚯蚓长度为x，神刀手会将其切成两只长度分别为!和的蚯蚓。特殊地，如果这两个数的其中一个等于0，则这个长度为0的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加q(是一个非负整常数)。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要m秒才能到来......

(m为非负整数）

蛐蛐国王希望知道这m秒内的战况。具体来说，他希望知道：

•m秒内，每一秒被切断的蚯蚓被切断前的长度（有m个数）

•m秒后，所有蚯蚓的长度（有n+m个数)。

蛐蛐国王当然知道怎么做啦！但是他想考考你......

输入输出格式

输入格式：

 

第一行包含六个整数n,m,q,u,v,t，其中：n,m,q的意义见【问题描述】；u,v,t均为正整数；你需要自己计算p=u/v(保证0<u<v)t是输出参数，其含义将会在【输出格式】中解释。

第二行包含n个非负整数，为，即初始时n只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证，，，，，。

 

输出格式：

 

第一行输出个整数，按时间顺序，依次输出第t秒，第2t秒，第3t秒……被切断蚯蚓（在被切断前）的长度。

第二行输出个整数，输出m秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第t，第2t，第3t……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要 输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

 

输入输出样例

输入样例#1：
3 7 1 1 3 1
3 3 2
输出样例#1：
3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2
输入样例#2：
3 7 1 1 3 2
3 3 2
输出样例#2：
4 4 5
6 5 4 3 2
输入样例#3：
3 7 1 1 3 9
3 3 2
输出样例#3：
//空行
2

说明

【样例解释1】

在神刀手到来前：3只蚯蚓的长度为3,3,2。

1秒后：一只长度为3的蚯蚓被切成了两只长度分别为1和2的蚯蚓，其余蚯蚓的长度增加了1。最终4只蚯蚓的长度分别为(1,2),4,3。括号表示这个位置刚刚有一只蚯蚓被切断

2秒后：一只长度为4的蚯蚓被切成了1和3。5只蚯蚓的长度分别为：2,3,(1,3),4。

3秒后：一只长度为4的蚯蚓被切断。6只蚯蚓的长度分别为：3,4,2,4,(1,3)。

4秒后：一只长度为4的蚯蚓被切断。7只蚯蚓的长度分别为：4,(1,3),3,5,2,4。

5秒后：一只长度为5的蚯蚓被切断。8只蚯蚓的长度分别为：5,2,4,4,(1,4),3,5。

6秒后：一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为：（1,4),3,5,5,2,5,4,6。

7秒后：一只长度为6的蚯蚓被切断。10只蚯蚓的长度分别为：2,5,4,6,6,3,6,5,(2,4)。所以，7秒内被切断的蚯蚓的长度依次为3,4,4,4,5,5,6。7秒后，所有蚯蚓长度从大到小排序为6,6,6,5,5,4,4,3,2,2

【样例解释2】

这个数据中只有t=2与上个数据不同。只需在每行都改为每两个数输出一个数即可。

虽然第一行最后有一个6没有被输出，但是第二行仍然要重新从第二个数再开始输出。

【样例解释3】

这个数据中只有t=9与上个数据不同。

注意第一行没有数要输出，但也要输出一个空行。

【数据范围】

 

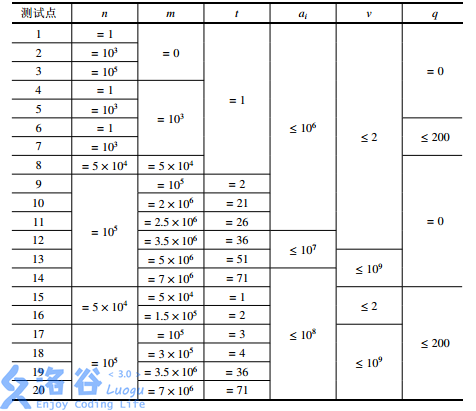
吐槽

　　为啥我这篇博文标题要特地写UOJ？因为UOJ的Extra Test很丧病的卡double的精度，u/v要long double才过得去，官方数据用double就够了。

　　这题被选做NOI2017练习赛T1，下午学习了一波，晚上被热的七荤八素，中暑成了CCF的孩～子……拖了3h才在洛谷上AC了这道题

解题思路

　　感觉这篇博文讲的挺好的http://www.cnblogs.com/ljh2000-jump/p/6189057.html//代码在BZOJ会被卡精度PE

　　证明单调性的方法是这题最有趣的地方，方法不唯一哦

源代码

//BZOJ、cogs会爆，不知为什么

#include<cmath>
#include<queue>
#include<cstdio>
#include<algorithm>

std::queue<long long> que[4];
int n,m,u,v,p,t;

int queue[100010]={0};
int main()
{
    //freopen("earthworm.in","r",stdin);
    //freopen("earthworm.out","w",stdout);
    scanf("%d%d%d%d%d%d",&n,&m,&p,&u,&v,&t);
    long double q=(long double)(u)/(long double)(v);
    for(int i=1,a;i<=n;i++)
        scanf("%d",&queue[i]);
    std::sort(queue+1,queue+n+1);
    for(int i=n;i>0;i--)
        que[1].push(queue[i]);
    long long base=0;
    for(int i=1;i<=m;i++)
    {
        long long qie=-2147483650;
        long long pos=0;
        for(int j=1;j<=3;j++)
        {
            if(!que[j].empty()&&que[j].front()>qie)
            {
                qie=que[j].front();
                pos=j;
            }
        }
        que[pos].pop();
        qie+=base;
        if(i%t==0) printf("%lld ",qie);
        long long q1=(int)((long double)qie*q),q2=qie-q1;
        base+=p;
        q1-=base;q2-=base;
        que[2].push(q2),que[3].push(q1);
    }
    printf("\n");
    
    for(int i=1,mx=n+m;i<=mx;i++)
    {
        long long qie=-2147483650;
        int pos=0;
        for(int j=1;j<=3;j++)
        {
            if(!que[j].empty()&&que[j].front()>qie)
            {
                qie=que[j].front();
                pos=j;
            }
        }
        que[pos].pop();
        if(i%t==0) printf("%lld ",qie+base);
    }
    return 0;
}

能在BZOJac的代码：http://blog.csdn.net/qzh_1430586275/article/details/53413950

posted @ 2017-07-18 21:29  wawcac  阅读(221)  评论(0)  编辑  收藏  举报