DP Training(Updating)♪(^∇^*)
DP Training
DP Training 01
https://vjudge.net/contest/220286 密码 nfls
A 数塔(Easy)
\(f[i][j]\) 表示当前选第 \(i\) 行,第 \(j\) 列的格子,上面的选完了,下面的没选的最大方案
\(f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]\)
B 数塔(Medium)
不难发现答案一定是交点到四个顶点的最大路径之和,预处理 \(f[4][i][j]\) 表示 \((i,j)\) 到四个定点的最优距离,然后枚举交点计算结果
注意有两种情况: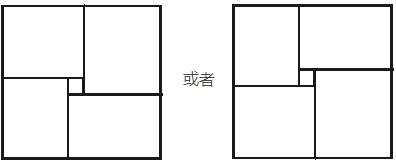
分别统计答案即可
C 数塔(Hard)
题目坏掉了
写了一个不知道真的假的
我们把来回想象成两个人一起从左上角走到右下角, \(f[i][j][k]\) 表示当前走到第 \(i\) 行,第一个人在第 \(j\) 列,第二个人在第 \(k\) 列,最大收益,转移的时候枚举第一个人是否是从左边来的,第二个人是否是从左边来的(否则就是从上边来的),复杂度 \(O(n^3)\)
D 最大连续和(Easy)
这个好像不用\(\text{dp}\),直接维护一个当前的和以及当前的和对应的左端点
每次如果当前和>=0,那么就加上现在这个数,否则当前和改成现在这个数,左端点改成现在的位置(显然前面的负数没有意义)
rep(i,1,n){
if(nw>=0 && nwl) nw+=a[i];
else nwl=i,nw=a[i];
if(nw>ans){ans=nw;ansl=nwl;ansr=i;}
}
E 最大连续和(Medium)
跟D一样的做法
首先枚举左边界和右边界,然后就把二维问题转化成了一维问题,每一个数就是对应的行的左边界与右边界之间数的和,然后用上面的方法求一下最大连续和即可,复杂度 \(O(n^3)\)
F 最大连续和(Hard)
垃圾题目
一眼看上去不可做,网上翻一下题解,复杂度 \(O(nm)\) ?题目中根本没有说明 \(m\) 的范围,我以为 \(m\) 可以达到\(1\text{e}6\)……
然后就好做了,想怎么做怎么做
先记一个 \(f[i][j]\) 表示当前选到第 \(i\) 个数,当前选了 \(j\) 段,最大的收益
转移就是
然后记录一个前缀MAX就可以做到 \(O(nm)\) 了,注意空间需要滚动数组优化
G 最长上升子序列(Easy)
\(O(n^2)\) 暴力dp。。。
H 最长上升子序列(Medium1)
可以证明答案就是LIS的长度
不过我用的是贪心的做法,维护一个set存储每一个拦截系统的上一个高度,每次把当前导弹赋给大于等于他的最小的那个,如果不存在,则新建一个导弹拦截系统。容易证明正确性。
注意多测。。。
I 最长上升子序列(Medium2)
把第一维排序,第二维跟着变换,求变换后的LIS
注意输出的时候road和roads不一样,而且king的首字母小写,两个test之间有一个换行。。。
J 最长公共子序列(Easy)
为什么HDU的题这么多都没有数据范围啊。。。
直接写显然是 \(O(nm)\) 的,然后把数组开到 \(5000 \times 5000\),就过了。。。
K 最长公共子序列(Medium)
跟上一题基本一样,不过有数据范围(😅)
L 最长公共子序列(Hard)
我们令 \(f[i][j]\) 表示 \(a\) 取前 \(i\) 个,\(b\) 取前 \(j\) 个的最长公共子序列,\(g[i][j]\) 表示 \(a\) 取前 \(i\) 个,\(b\) 取前 \(j\) 个的种数,转移:若 \(f[i - 1][j] == f[i][j]\),则 \(g[i][j] += g[i - 1][j]\),表示 \(i\) 这个字符不选;再考虑选 \(i\) 这个字符,找到 \(b\) 串前 \(j\) 个字符中最靠后的与 \(a[i]\) 匹配的字符的位置,设为 \(p\),若 \(f[i - 1][p - 1] + 1 == f[i][j]\),则 \(g[i][j] += g[i - 1][p - 1]\)。最终的答案即为 \(f[n][m]\)。复杂度 \(O(n^2)\)。
(多测!多测!因为数组没清零挂了1h+。。。)
M 0/1背包(Easy)
最基础的背包问题,——但是
注意!!!背包容量可以为零!!!物品的体积也可以为零!!!
(怎么这种模板题总要坑你一下才高兴啊。。。😡)
N 0/1背包(Medium1)
题目又一次坏掉了,好像FZU这个OJ不能用了。。。
依旧是基础的背包问题
注意到value比较小,我们用 \(f[i][j]\) 表示当前选到第 \(i\) 个物品,当前的 \(\text{value}\) 总和为 \(j\) 的最小 \(\text{weight}\),那么我们转移就枚举当前这个用不用,然后算答案的时候就看最大的满足 \(f[n][x] \le B\) 的 \(x\) 就可以了
O 0/1背包(Medium2)
以为 \(\text{poj}\) 特别的慢,一开始不知道怎么做,后来发现就是直接上 \(100 \times 100 \times 2000\) 的做法,暴力 \(\text{dp}\),注意 \(\text{long long}\) 就超时了,\(\text{int}\) 才能过
P 0/1背包(Hard)
真的Hard吗。。。
既然要求第 \(k\) 大的和,我们就维护前 \(k\) 大,然后暴力合并,就是把可能的 \(2k\) 种拎出来,\(sort\) 一下,去个重,然后放进当前的 \(dp\) 数组里
注意 \(set\) 会超时(不开 \(O2\) 的垃圾 \(\text{OJ}\)),必须用 \(sort\) 加上 \(unique\)
然后我们要从大到小排序,一种写法是 \(\text{sort + reverse}\),另一种是 \(\text{sort(a+1,a+n+1,greater<int>())}\) ,看起来没有区别,结果第二种比第一种快四倍以上。。。
Q 完全背包(Easy)
\(f[i][j]\) 表示当前选到前 \(i\) 种硬币,总重量正好是 \(j\) 的最小总价值
转移 \(f[i][j]=\min(f[i-1][j],f[i][j-w[i]]+v[i])\)
R 完全背包(Medium)
正常的完全背包,但是注意到大于 \(k\) 也是可行的,所以需要写成递推的形式
另:完全背包可以用一个一维数组实现,每一次直接递推更新,正确性显然,而且好写
S 完全背包(Hard)
我们先假设度数都是1,我们要把其中某些点度数增大,增大的部分总和为 \(n-2\),那么就设 \(h(i, j)\) 表示 \(\leq i\) 的点已经考虑了,已经增大了 \(j\)。转移就是 \(h(i, j) = \max \{ h(i - 1, j), h(i, j - (i - 1)) + f(i) - f(1) \}\)
这个方法的巧妙之处就在于,不需要知道具体增大了多少点,因为大家加起来只有 \((n - 2)\),是肯定不会超过 \(n\) 个的。
以上by叉姐
实质上就是把问题转化为容量为 \(n-2\) 的背包,“增加度数为 \(i\) 的点”看作物品,价值就是 \(f[i]-f[1]\)
因为一个物品想要多少就有多少(在小于等于背包容量的时候一定能够取到这么多物品),所以就变成了完全背包问题
DP Training 02
https://vjudge.net/contest/220287 密码 nfls
C 思维
\(f[i][j]\) 表示当前选了前 \(i\) 个数,当前的模数为 \(j\) 是否可行
转移就是枚举当前数加还是减
D 思维
首先行不能交换,最终答案矩形对应着行上的一段区间,我们枚举一个行作为答案的底端
然后可以维护 \(h[i]\) 表示当前行第 \(i\) 列对应的高度是多少,高度指的是这一列以第 \(i\) 行为底端的最长的柱形的 \(1\) 的数量
那么我们肯定是把 \(h[i]\) 大的放在一起,统计一下 \(h[i] \ge k\) 的 \(i\) 有多少个,然后就算一下答案就好了


