2017国家集训队作业Atcoder题目试做
2017国家集训队作业Atcoder题目试做
虽然远没有达到这个水平,但是据说Atcoder思维难度大,代码难度小,适合我这种不会打字的选手,所以试着做一做
不知道能做几题啊
在完全自己做出来的题前面打"√“(目前好像还没有诶。。。o(╥﹏╥)o)
计数器菌:4/104
agc001_d
如果两个字符确定相等就在中间连一条边,那么所有字符相同就等价于使整个图联通
然后发现至少要\(n-1\)条边,而事实上一个序列贡献的边数最大为\(\frac n 2\)条,而且一旦序列里有一个奇数贡献的边数就会减去\(\frac 1 2\),所以如果原始序列出现\(\gt 2\)个奇数,那么就不可行
一个偶数序列,整体向左平移一个之后,正好全部连起来了
如果有奇数怎么办?因为至多两个奇数,我们把奇数放到两边,中间全是偶数,那么可以像刚才那样做,两边的奇数这样做也符合题意。
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<iostream>
#include<queue>
#include<string>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<long long,long long> pll;
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define rep(i,j,k) for(register int i=(int)(j);i<=(int)(k);i++)
#define rrep(i,j,k) for(register int i=(int)(j);i>=(int)(k);i--)
ll read(){
ll x=0,f=1;char c=getchar();
while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int maxn=200;
int n,m;
int a[maxn];
int main(){
#ifdef LZT
// freopen("in","r",stdin);
#endif
int num=0;
n=read();m=read();
rep(i,1,m){
a[i]=read();
if(a[i]&1) num++;
}
if(num>2){
puts("Impossible");
return 0;
}
for(int i=1;i<=m;i++)
if(a[i]&1){
if(a[1]&1) swap(a[i],a[m]);
else swap(a[i],a[1]);
}
rep(i,1,m) cout<<a[i]<<' ';
cout<<endl;
a[1]++;a[m]--;
if(a[m]==0) m--;
if(m>=2){
cout<<m<<endl;
rep(i,1,m) cout<<a[i]<<' ';
cout<<endl;
}
else{
if(n<=2){
cout<<1<<endl;
cout<<n<<endl;
}
else{
cout<<2<<endl;
cout<<n-1<<' '<<1<<endl;
}
}
return 0;
}
agc001_e
我们发现答案其实就是要求\(\sum_{i=1}^{n-1}\sum_{j=i+1}^nC_{a_i+a_j+b_i+b_j}^{a_i+a_j}\)
然后知道\(C_{a_i+a_j+b_i+b_j}^{a_i+a_j}\)实际上就是点\((-a_i,-b_i)\)走到\((a_j,b_j)\)的方案数
那么原式等价于求点集\((-a_i,-b_i)\)到点集\((a_i,b_i)\)两两的方案数的和减去所有点走到他对应的对称点的方案数(即\(i=j\)的方案数)除以2(每个方案被算了两次)
所以dp就可以了,可以想象中建立一个超级源点连向所有的\((-a_i,-b_i)\)和超级汇点连向所有的\((a_i,b_i)\),就可以求出方案数
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<iostream>
#include<queue>
#include<string>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<long long,long long> pll;
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define rep(i,j,k) for(register int i=(int)(j);i<=(int)(k);i++)
#define rrep(i,j,k) for(register int i=(int)(j);i>=(int)(k);i--)
ll read(){
ll x=0,f=1;char c=getchar();
while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int mod=1000000007;
const int maxn=200200;
const int maxm=2200;
int n;
int a[maxn],b[maxn];
int dp[maxm*2][maxm*2];
int flag[maxm*2][maxm*2];
int ans;
void pl(int &a,ll b){
a=(a+b%mod)%mod;
}
void mi(int &a,ll b){
a=a-b%mod;
while(a<0) a+=mod;
a=a%mod;
}
int main(){
#ifdef LZT
freopen("in","r",stdin);
#endif
n=read();
rep(i,1,n) a[i]=read(),b[i]=read();
rep(i,1,n){
flag[2100-a[i]][2100-b[i]]++;
flag[a[i]+2100][b[i]+2100]++;
}
rep(i,1,4200){
rep(j,1,4200){
pl(dp[i][j],dp[i-1][j]);
pl(dp[i][j],dp[i][j-1]);
if(flag[i][j] && i<=2100 && j<=2100) pl(dp[i][j],flag[i][j]);
if(flag[i][j] && i>=2100 && j>=2100) pl(ans,dp[i][j]*1ll*flag[i][j]);
}
}
memset(dp,0,sizeof(dp));
dp[0][0]=1;
rep(i,0,4200){
rep(j,0,4200){
if(i==0 && j==0) continue;
if(i) pl(dp[i][j],dp[i-1][j]);
if(j) pl(dp[i][j],dp[i][j-1]);
}
}
rep(i,1,n)
mi(ans,dp[a[i]+a[i]][b[i]+b[i]]);
ans=ans*500000004ll%mod;
cout<<ans<<endl;
return 0;
}
agc002_d
先考虑暴力做法,对于一组询问\((x,y,z)\),我们暴力将边从小到大加入图里,当\(x\)所在的连通块点数加\(y\)所在连通块点数(当\(x\)和\(y\)在不同连通块时才加)第一次\(\geq z\)时,当前边的序号就是答案
所以答案是有单调性的,可以二分
然后每一组都二分肯定不行,所以整体二分
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<iostream>
#include<queue>
#include<string>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<long long,long long> pll;
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define rep(i,j,k) for(register int i=(int)(j);i<=(int)(k);i++)
#define rrep(i,j,k) for(register int i=(int)(j);i>=(int)(k);i--)
ll read(){
ll x=0,f=1;char c=getchar();
while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int maxn=100100;
int n,m,Q;
pii edge[maxn];
struct query
{
int ind;
int a,b,num;
void re(int x){
a=read(),b=read(),num=read();
ind=x;
}
} q[maxn],tmp[maxn];
int ans[maxn],fa[maxn],sz[maxn];
bool ok[maxn];
pii sta[maxn];int cnt;
inline int fp(int x){if(x==fa[x]) return x;return fp(fa[x]);}
void solve(int l,int r,int le,int ri){
//cout<<l<<' '<<r<<' '<<le<<' '<<ri<<endl;
if(l==r){
rep(i,le,ri) ans[q[i].ind]=l;
int x=edge[l].fi,y=edge[l].se;
x=fp(x);y=fp(y);
if(x!=y){
if(sz[x]>sz[y])swap(x,y);
fa[x]=y;sz[y]+=sz[x];
}
return;
}
int md=(l+r)>>1;cnt=0;
rep(i,l,md){
int x=edge[i].fi,y=edge[i].se;
x=fp(x);y=fp(y);
if(x!=y){
if(sz[x]>sz[y]) swap(x,y);
fa[x]=y;sz[y]+=sz[x];
sta[++cnt]=mp(x,y);
}
}
rep(i,le,ri){
query &nw=q[i];
int a=nw.a,b=nw.b;
//cout<<a<<' '<<b<<endl;
a=fp(a);b=fp(b);
//cout<<i<<' '<<a<<' '<<b<<' ';
int nww=0;
if(a==b) nww=sz[a];else nww=sz[a]+sz[b];
if(nww>=nw.num) ok[i]=1;else ok[i]=0;
//cout<<ok[i]<<endl;
}
int pos=le-1;
rep(i,le,ri)
if(ok[i]) tmp[++pos]=q[i];
pos=ri+1;
rrep(i,ri,le)
if(!ok[i]) tmp[--pos]=q[i];
//cout<<le<<' '<<ri<<' '<<pos<<endl;
rep(i,le,ri) q[i]=tmp[i];
while(cnt){
int x=sta[cnt].fi,y=sta[cnt].se;
fa[x]=x;sz[y]-=sz[x];cnt--;
}
solve(l,md,le,pos-1);solve(md+1,r,pos,ri);
}
int main(){
n=read(),m=read();
rep(i,1,m) edge[i].fi=read(),edge[i].se=read();
Q=read();
rep(i,1,Q) q[i].re(i);
rep(i,1,n) sz[i]=1,fa[i]=i;
solve(1,m,1,Q);
rep(i,1,Q) printf("%d\n",ans[i]);
return 0;
}
/*
5 6
2 3
4 5
1 2
1 3
1 4
1 5
6
2 4 3
2 4 4
2 4 5
1 3 3
1 3 4
1 3 5
*/
agc002_e
真难想的博弈题
首先先想状态
不知怎么想到把他表示成图形
就是我们先排序 然后把一堆石子想象成一个石子个数*1的矩形。 把矩形从高到低排列变成一个图形。
然后操作就变成了删掉最左边一列或者最下面一行
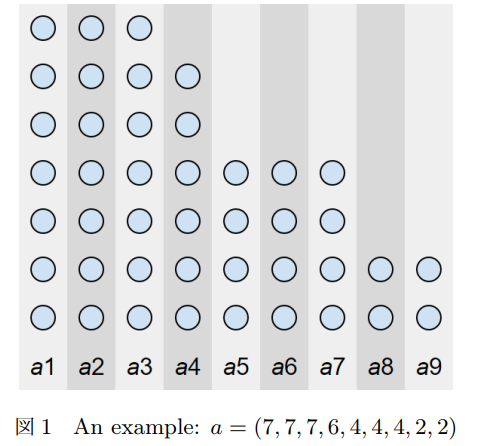
假设有一个点当前在\((1,1)\),那么每次操作他向右或者向上移动一个,不能移动者输
那么给每个点标记上\(o\)或者\(x\),分别表示必胜和必败
所有最外层的角上(意会)一定都是\(x\)
然后发现当\((x+1,y+1)\)不是最外层的点的时候,\((x,y)\)和\((x+1,y+1)\)的标记相同
所以算法就是先把\((1,1)\)向右上方移动直到边界为止,然后要么向上要么向右,如果都是必败那么就是必败,否则必胜
向上向右因为只有一个方向所以只奇偶性有关
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<iostream>
#include<queue>
#include<string>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
typedef long double ld;
typedef unsigned long long ull;
typedef pair<long long,long long> pll;
#define fi first
#define se second
#define pb push_back
#define mp make_pair
#define rep(i,j,k) for(register int i=(int)(j);i<=(int)(k);i++)
#define rrep(i,j,k) for(register int i=(int)(j);i>=(int)(k);i--)
ll read(){
ll x=0,f=1;char c=getchar();
while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();}
return x*f;
}
const int maxn=100100;
int n;
int a[maxn];
int main(){
n=read();
rep(i,1,n) a[i]=read();
sort(a+1,a+n+1);
reverse(a+1,a+n+1);
rep(i,1,n+1){
if(a[i]<i){
i--;
int num=0;
for(int j=i+1;j<=n;j++)
if(a[j]==i) num++;
if(num&1){
puts("First");
return 0;
}
if((a[i]-i)&1) puts("First");
else puts("Second");
return 0;
}
}
}

