bzoj 5019 [Snoi2017]遗失的答案
题面
https://www.lydsy.com/JudgeOnline/problem.php?id=5019
题解
如果L不是G的倍数 答案为0
下面考虑G|L的情况
将G,L质因数分解
设$L=p_1^{l_1} \times p_2^{l_2} \times ... \times p_t^{l_t}$
那么G的所有质因数肯定在$p_1 ~ p_t$之间 所以我们可以把G也写成
$G=p_1^{g_1} \times p_2^{g_2} \times ... \times p_t^{g_t}$
那么我们选的数![]() 满足以下条件:
满足以下条件:
1. ![]()
2. 我们把ai质因数分解
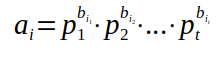
bi是一个数组 记录了ai质因数分解后每一项的次数
那么我们有
![]()
![]()
根据条件1, 我们得出能够选的数不超过800个, 可以处理出来,放进数组a中
根据条件2, 我们可以状压dp
令dp[i][mask]表示当前考虑到第i个数,当前状态为mask的方案数
mask一共2*t位 其中第2*i-1位表示当前选的数的集合能否满足$min(b_{j_i})=g_i$
第2*i为表示当前选的数的集合能否满足$max(b_{j_i})=l_i$
那么当mask全为1的时候就满足题意了
那么对于一个数x,包含x的满足题意的方案数=总数-不包含x的方案数
总数已经得到,就是dp[n][mxst]
不包含x的方案数如何求呢
令dp2[i][mask]表示倒着做 当前第i个数,状态为mask的方案数
那么ans[i]=sum(dp[i-1][state]*dp[i+1][state2],state|state2=mxst)
这个做法复杂度O(800*mxst*mxst) 超时
我们要去掉一个mxst
如果我们能够处理出f[i][st]表示倒着考虑到第i个数,当前的状态包含了st的方案数
那么ans[i]=sum(dp[i-1][state]*f[i+1][mxst-state]) 就可以了
我们可以用一种奇妙的方法从dp2处理出f 具体见代码
Code
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 5 ll read(){ 6 ll x=0,f=1;char c=getchar(); 7 while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();} 8 while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();} 9 return x*f; 10 } 11 12 const int mod=1e9+7; 13 int n,G,L,Q; 14 int pr[20],cnt,num[20],mi[20]; 15 int num2[20],mi2[20]; 16 int a[1000],tot,ok[1000]; 17 int dp1[800][70000],dp2[800][70000]; 18 map<int,int> ans; 19 20 inline void pl(int &a,int b){ 21 a=a+b;if(a>mod) a-=mod; 22 } 23 24 int main(){ 25 #ifdef LZT 26 freopen("in","r",stdin); 27 #endif 28 n=read();G=read();L=read();Q=read(); 29 if(L%G){ 30 while(Q--) 31 puts("0"); 32 return 0; 33 } 34 int t=L; 35 for(int i=2;i<=t;i++){ 36 if(t%i) continue; 37 pr[++cnt]=i,mi[cnt]=1; 38 while(t%i==0) t=t/i,num[cnt]++,mi[cnt]*=i; 39 } 40 if(t!=1){pr[++cnt]=t,num[cnt]=1,mi[cnt]=t;} 41 t=G; 42 for(int i=1;i<=cnt;i++){ 43 mi2[i]=1; 44 while(t%pr[i]==0){ 45 t=t/pr[i]; 46 num2[i]++; 47 mi2[i]*=pr[i]; 48 } 49 } 50 for(int i=1;i*G<=L && i*G<=n;i++) 51 if((L/G)%i==0) a[++tot]=i*G; 52 for(int i=1;i<=tot;i++){ 53 int nw=a[i]; 54 for(int j=cnt;j>=1;j--){ 55 ok[i]<<=1;if(nw%mi[j]==0) ok[i]|=1; 56 ok[i]<<=1;if((nw/mi2[j])%pr[j]) ok[i]|=1; 57 } 58 } 59 int mxst=(1<<(2*cnt))-1; 60 for(int i=1;i<=tot;i++){ 61 dp1[i-1][0]=1; 62 for(int st=0;st<=mxst;st++){ 63 pl(dp1[i][st],dp1[i-1][st]); 64 if(dp1[i-1][st]) pl(dp1[i][st|ok[i]],dp1[i-1][st]); 65 } 66 } 67 for(int i=tot;i>=1;i--){ 68 dp2[i+1][0]=1; 69 for(int st=0;st<=mxst;st++){ 70 pl(dp2[i][st],dp2[i+1][st]); 71 if(dp2[i+1][st]) pl(dp2[i][st|ok[i]],dp2[i+1][st]); 72 } 73 } 74 75 ans[a[1]]=(dp1[tot][mxst]-dp2[2][mxst]+mod)%mod; 76 ans[a[tot]]=(dp1[tot][mxst]-dp1[tot-1][mxst]+mod)%mod; 77 //处理f 78 for(int i=1;i<=tot;i++){ 79 for(int k=0;k<(2*cnt);k++){ 80 for(int st=0;st<=mxst;st++){ 81 if((st&(1<<k))==0) 82 pl(dp2[i][st],dp2[i][st|(1<<k)]); 83 } 84 } 85 } 86 for(int i=2;i<tot;i++){ 87 int nw=0; 88 for(int st=0;st<=mxst;st++){ 89 int rem=((1<<(2*cnt))-1)-st; 90 pl(nw,dp1[i-1][st]*1ll*dp2[i+1][rem]%mod); 91 } 92 ans[a[i]]=(dp1[tot][mxst]-nw+mod)%mod; 93 } 94 while(Q--){ 95 int x=read(); 96 printf("%d\n",ans[x]); 97 } 98 99 return 0; 100 } 101 102 /* 103 5 1 30 104 5 105 1 2 3 4 5 106 */
Review
动机?
分解质因数是显然的
然后对于这种满足最小公倍数等于什么或者最大公约数等于什么的题目我们应该自然地想到每一个质因数分开处理
然后对于这种满足最小公倍数等于什么并且最大公约数等于什么的题目我们应该自然地想到状压dp
至于那个处理部分 就只能靠积累了
处理部分的正确性证明:
对于两个状态st1,st2 假设st1∈st2
假设st2中比st1多出来的分别在第a1,a2,...,ak位 并且a1<a2<...<ak
那么会发生以下过程
f[st2-(1<<a1)]+=f[st2]
f[st2-(1<<a1)-(1<<a2)]+=f[st2-(1<<a1)]
...
f[st1]=f[st2-(1<<a1)-(1<<a2)-...-(1<<ak)]+=f[st2-(1<<a1)-(1<<a2)-...-(1<<a(k-1))]
这样st2的值被加进了st1中
所以这个过程是正确的
(UPD: 这个处理被称为Fast Zeta Transform 快速ζ变换)(真是有趣 一天做到两道用到这个的题)


