bzoj 4816 [Sdoi2017]数字表格
题面
https://www.lydsy.com/JudgeOnline/problem.php?id=4816
题解
显然是莫比乌斯反演
首先得出
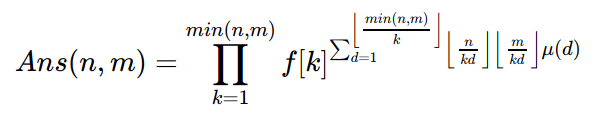
然后发现 我们要把d提出去
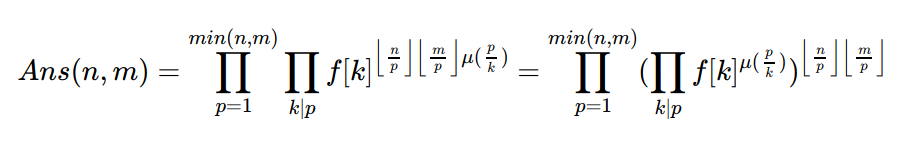
这样就好做了
跟SDOI2015的一道题类似
因为 $\left \lfloor \frac{n}{p} \right \rfloor \left \lfloor \frac{m}{p} \right \rfloor$只有$(\sqrt n +\sqrt m)$种取值 并且$\prod_{k|p} f[k]^{\mu(\frac{p}{k})}$对于每个p都是固定的
所以我们可以预处理$\prod_{k|p} f[k]^{\mu(\frac{p}{k})}$的前缀积 以及前缀积的逆元 这样可以方便的算出区间的乘积
然后对于每一组询问 我们枚举$(\sqrt n +\sqrt m)$种取值 就可以得出结果
Code

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 5 ll read(){ 6 ll x=0,f=1;char c=getchar(); 7 while(c<'0' || c>'9'){if(c=='-')f=-1;c=getchar();} 8 while(c>='0' && c<='9'){x=x*10+c-'0';c=getchar();} 9 return x*f; 10 } 11 12 const int maxn=1000100; 13 const int mod=1e9+7; 14 int mu[maxn],pr[maxn],cnt; 15 bool isp[maxn]; 16 int fib[maxn],g[maxn],G[maxn],invG[maxn]; 17 int fpw[maxn][3]; 18 19 int ksm(int a,int b){ 20 int ret=1; 21 for(int i=0;i<=30;i++){ 22 if(b&1) ret=ret*1ll*a%mod; 23 a=a*1ll*a%mod; 24 b=b>>1; 25 if(b==0) return ret; 26 } 27 } 28 29 int inv(int a){ 30 return ksm(a,mod-2); 31 } 32 33 int main(){ 34 #ifdef LZT 35 freopen("in","r",stdin); 36 #endif 37 mu[1]=1; 38 memset(isp,1,sizeof(isp)); 39 for(int i=2;i<=1000000;i++){ 40 if(isp[i]){ 41 pr[++cnt]=i; 42 mu[i]=-1; 43 } 44 for(int j=1;j<=cnt && i*pr[j]<=1000000;j++){ 45 isp[i*pr[j]]=0; 46 if(i%pr[j]==0) break; 47 mu[i*pr[j]]=-mu[i]; 48 } 49 } 50 51 fib[1]=1; 52 for(int i=2;i<=1000000;i++) 53 fib[i]=(fib[i-1]+fib[i-2])%mod; 54 for(int i=1;i<=1000000;i++){ 55 fpw[i][0]=inv(fib[i]); 56 fpw[i][1]=1; 57 fpw[i][2]=fib[i]; 58 } 59 60 for(int i=1;i<=1000000;i++){ 61 g[i]=1; 62 for(int k=1;k*k<=i;k++){ 63 if(i%k) continue; 64 g[i]=g[i]*1ll*fpw[k][mu[i/k]+1]%mod; 65 if(k*k!=i) g[i]=g[i]*1ll*fpw[i/k][mu[k]+1]%mod; 66 } 67 } 68 G[0]=1; 69 for(int i=1;i<=1000000;i++) 70 G[i]=G[i-1]*1ll*g[i]%mod; 71 72 invG[0]=1; 73 for(int i=1;i<=1000000;i++) 74 invG[i]=inv(G[i]); 75 76 int tc=read(); 77 while(tc--){ 78 int n=read(),m=read(); 79 int j; 80 int ans=1; 81 for(int i=1;i<=min(n,m);i=j+1){ 82 j=min(n/(n/i),m/(m/i)); 83 ans=ans*1ll*ksm(G[j]*1ll*invG[i-1]%mod,(n/i)*1ll*(m/i)%(mod-1))%mod; 84 } 85 printf("%d\n",ans); 86 } 87 88 return 0; 89 }
Review
推导不成功 我自己没有推出来
枚举取值的写法:
1 int j; 2 for(int i=1;i<=min(n,m);i=j+1){ 3 j=min(n/(n/i),m/(m/i)); 4 //...... 5 }


