[CQOI2017]老C的方块
[CQOI2017]老C的方块
[题目链接]
[思路要点]
首先神仙染色

这样四种颜色染色,可以发现,所有的奇怪图形都是可以表示成 黄 -> 红 -> 蓝 -> 绿 这样顺序的一个四个格子的连通块
这样可以建一个分层图,让每个黄点向 \(S\) 连边,绿点向 \(T\) 连边,然后红黄,蓝绿之间的边权设为 \(\text{inf}\),中间的边如图所示
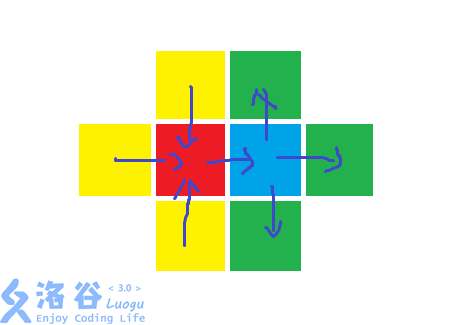
这个样子跑一个最小割就好了
然后注意一下坐标是 \(1e5\) 范围,所以按行和列的 \(\mod 4\) 的值进行分类即可
[代码]
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#include<queue>
#include<map>
#define LL long long
using namespace std;
const int mx[5]={0,-1,0,1,0};
const int my[5]={0,0,-1,0,1};
const int INF=0x3f3f3f3f;
const int mxn=300010;
int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct edge{
int v,nxt,f;
}e[mxn<<2];
int hd[mxn],mct=1;
void add_edge(int u,int v,int w){
e[++mct].v=v;e[mct].nxt=hd[u];e[mct].f=w;hd[u]=mct;return;
}
int S,T;
void insert(int u,int v,int w){
// printf("u:%d v:%d w:%d\n",u,v,w);
add_edge(u,v,w);
add_edge(v,u,0);
}
int d[mxn];
bool BFS(){
queue<int>q;
memset(d,0,sizeof d);
q.push(S);
d[S]=1;
while(!q.empty()){
int u=q.front();q.pop();
for(int i=hd[u];i;i=e[i].nxt){
int v=e[i].v;
if(!d[v] && e[i].f){
d[v]=d[u]+1;
q.push(v);
}
}
}
return d[T];
}
int DFS(int u,int lim){
if(u==T)return lim;
int f=0,tmp;
for(int i=hd[u];i;i=e[i].nxt){
int v=e[i].v;
if(d[v]==d[u]+1 && e[i].f && (tmp=DFS(v,min(lim,e[i].f)))){
f+=tmp;lim-=tmp;
e[i].f-=tmp;
e[i^1].f+=tmp;
if(!lim)return f;
}
}
d[u]=0;
return f;
}
LL Dinic(){
LL res=0;
while(BFS())res+=DFS(S,INF);
return res;
}
//
int PD(int x,int y){//判断是否在关键边旁边
if(y%4==0){
if((x&1)==0)return 2;//right
else return 4;//outpos
}
if(y%4==1){
if(x&1)return 1;//left
else return 4;//outpos
}
if(y%4==2){
if(x&1)return 2;//right
else return 3;//inpos
}
if(y%4==3){
if((x&1)==0)return 1;//left
else return 3;//inpos
}
return 0;
}
map<pair<int,int>,int>mp;
struct block{
int x,y;
int w;
}b[mxn];
int C,R,n;
int Tct[mxn];
void Build(int id){
// printf("insert:#%d\n",id);
int s=PD(b[id].x,b[id].y);
for(int k=1;k<=4;k++){
int nx=b[id].x+mx[k];
int ny=b[id].y+my[k];
if(nx>0 && nx<=R && ny>0 && ny<=C){
int v=mp[make_pair(nx,ny)];
if(!v)continue;
int t=PD(nx,ny);
/* printf("u:%d v:%d s:%d t:%d\n",id,v,s,t);
printf("x1:%d y1:%d x2:%d y2:%d\n",
b[id].x,b[id].y,nx,ny);
printf("s:%d t:%d\n\n",s,t);*/
if(s==1 && t==2){
add_edge(id,v,min(b[id].w,b[v].w));
add_edge(v,id,min(b[id].w,b[v].w));
}
if(s==2 && t==1){
add_edge(id,v,min(b[id].w,b[v].w));
add_edge(v,id,min(b[id].w,b[v].w));
}
if(s==1 && t==3){
insert(S,v,INF);
insert(v+n,id,INF);
}
if(s==1 && t==4){
insert(id,v,INF);
insert(v+n,T,INF);
}
if(s==2 && t==3){
insert(S,v,INF);
insert(v+n,id,INF);
}
if(s==2 && t==4){
insert(id,v,INF);
insert(v+n,T,INF);
}
if(s==3 && t==1){
insert(S,id,INF);
insert(id+n,v,INF);
}
if(s==3 && t==2){
insert(S,id,INF);
insert(id+n,v,INF);
}
if(s==4 && t==1){
insert(id+n,T,INF);
insert(v,id,INF);
}
if(s==4 && t==2){
insert(id+n,T,INF);
insert(v,id,INF);
}
}
}
mp[make_pair(b[id].x,b[id].y)]=id;
// printf("\n");
return;
}
void solve(){
for(int i=1;i<=n;i++){
int t=PD(b[i].x,b[i].y);
if(t==1 || t==2)continue;
add_edge(i,i+n,b[i].w);
add_edge(i+n,i,0);
}
LL res=Dinic();
printf("%lld\n",res);
return;
}
int main(){
int i,j;
C=read();R=read();n=read();
for(i=1;i<=n;i++){
b[i].y=read();b[i].x=read();
b[i].w=read();
}
S=0;T=n*2+1;
for(i=1;i<=n;i++)Build(i);
solve();
return 0;
}

