互斥事件与独立事件的区别

以抛一枚硬币为例，一次试验只有两种可能，Ω = {正面，反面}，这两种可能是互斥的，不可能同时发生，一种可能也可以说一个事件发生了，就湮灭了另一个事件发生的可能性。

所以，说两个事件互斥，也就意味着在一次试验当中，这两个事件不会同时发生，即P(AB) = 0，两者没有交集。

但是两个事件相互独立吗？一个事件影响另一个事件的发生吗？当然，影响到一个事件发生了另一个事件就不会发生的程度，所以两者不是独立事件！

 

 

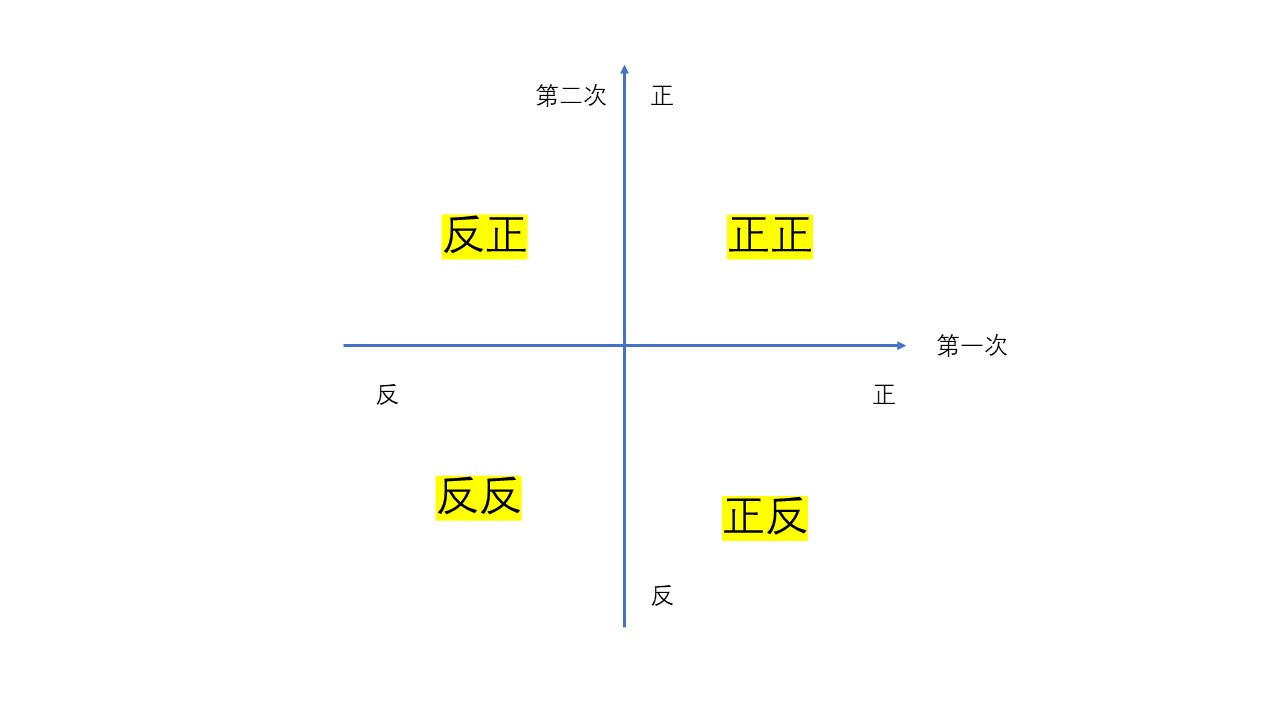
 那什么是独立事件呢？还是以抛硬币为例，我们抛两次硬币，总共有四种可能，Ω1 = {(正正),(正反),(反正),(反反)}，这个试验中我们可以定义很多事件，

比如事件A = (正正)，事件B = (正反)， 事件C = (反正)，事件D = (反反)，这四个事件两两互为互斥事件，发生了一个就不会再发生另一个。

又比如事件E = (第一次为正面)，事件F = (第一次为反面)，事件G = (第二次为正面)，事件F = (第二次为反面)，这四个事件又构成了一个新的样本空间，

此时，事件E和事件F为互斥事件，事件E和事件G为独立事件，但可以同时发生，构成了上面的样本空间Ω中的一个随机变量