数据降维_矩阵分析笔记

1、线性代数的正确打开的方式，解方程，从行视图的角度

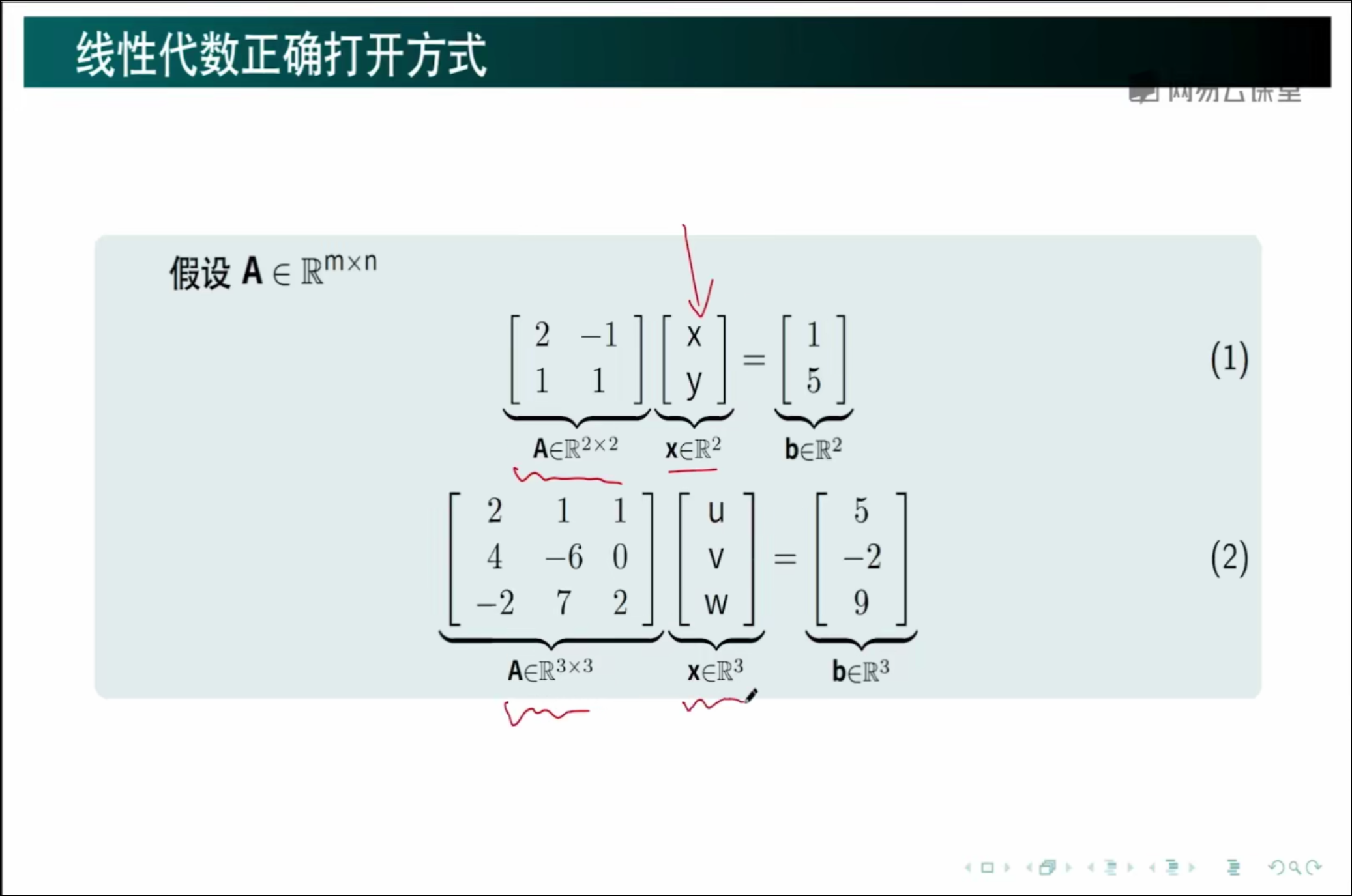
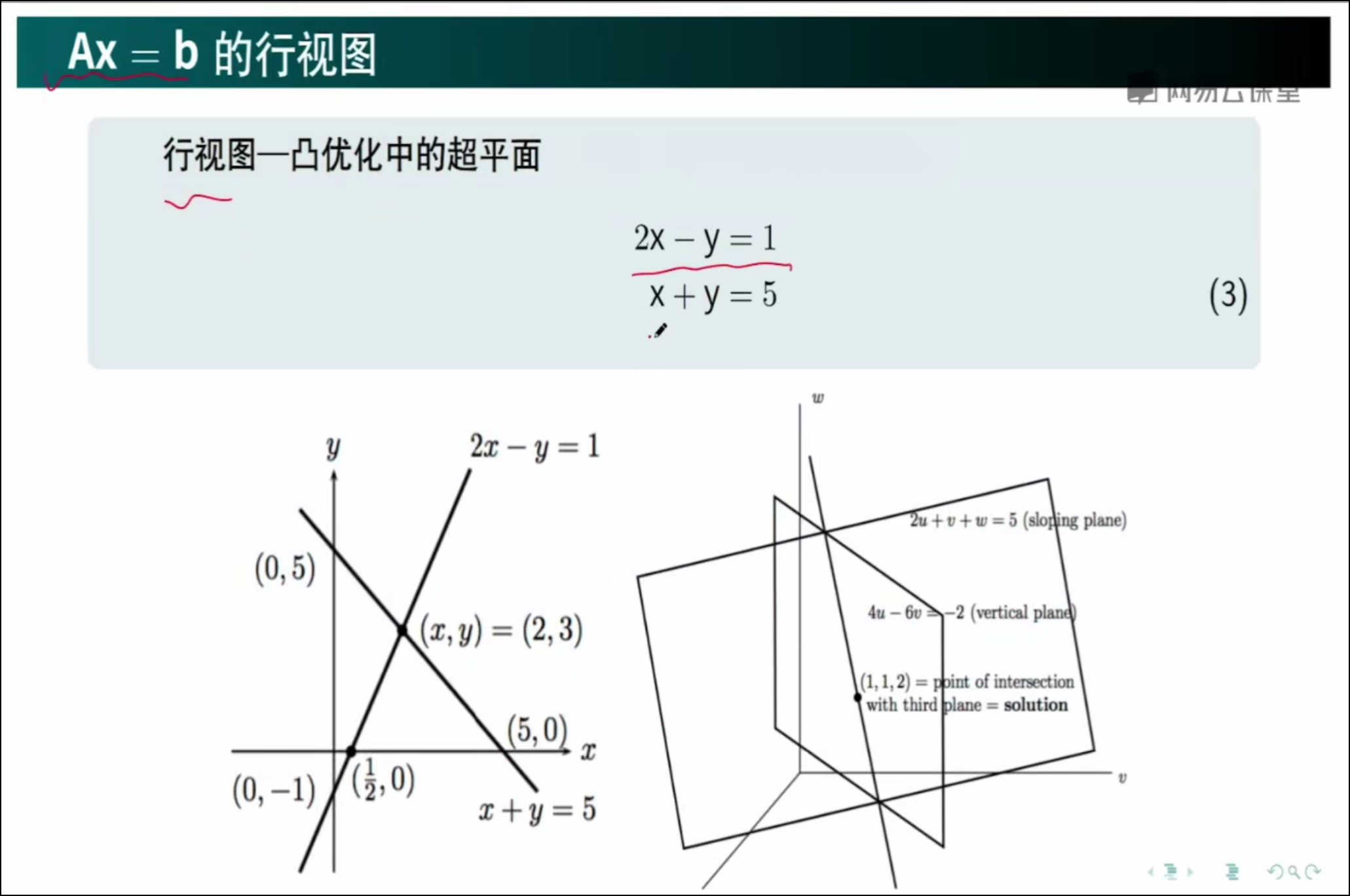
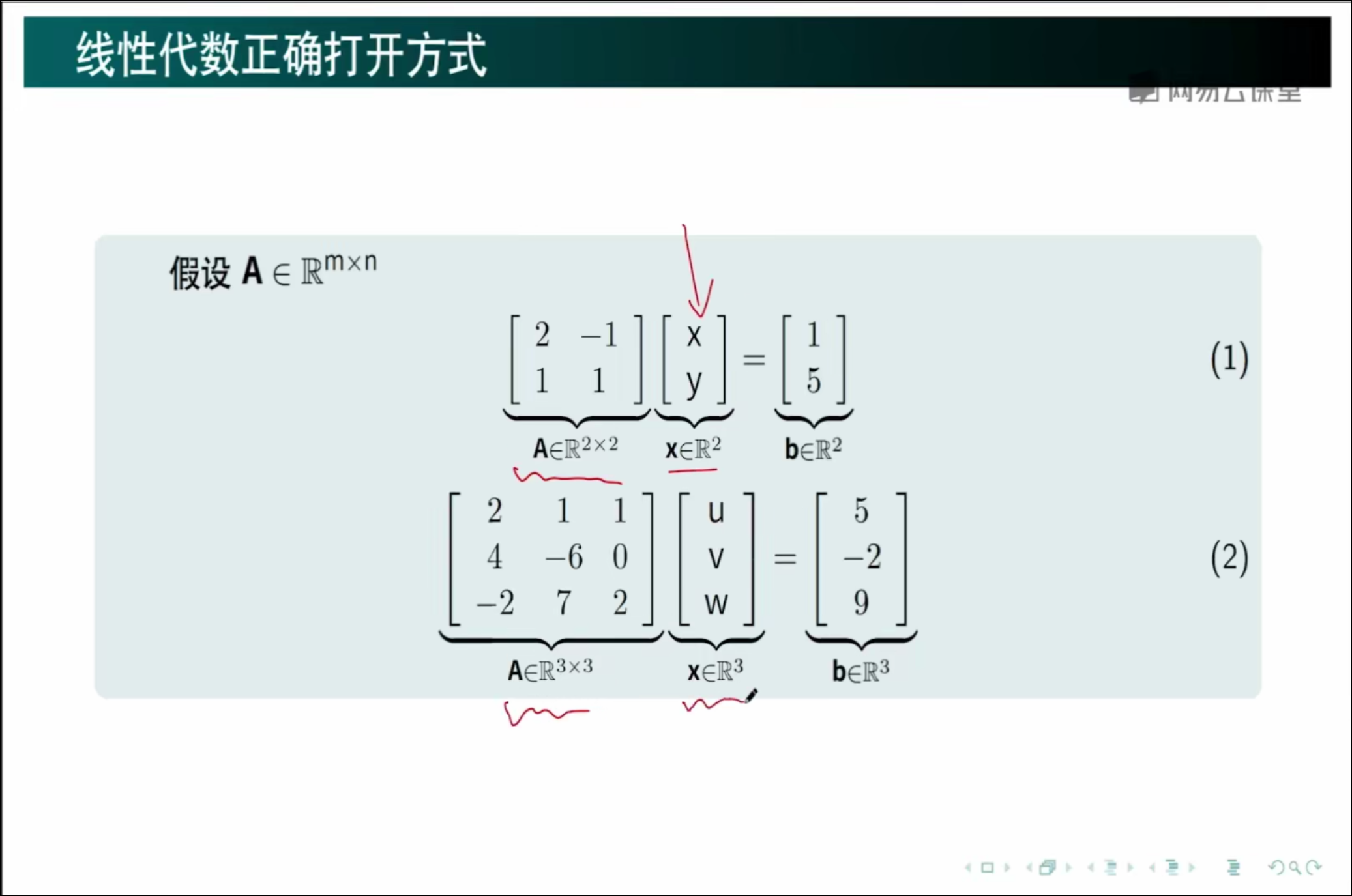
2、线性代数的正确打开的方式，解方程，从列视图的角度

 

3、矩阵的线性相关和线性无关

一个矩阵是由多个向量组成的，如果这些向量通过乘以一个系数，然后再相加后等于零，也就是说，存在至少一个向量，可以由其余向量表示出来，就说这些向量是线性相关的。

因为A矩阵中的向量是线性相关的，所以仅仅由前两个向量就可以表示（第三个向量可以由前两个线性表示，第三个没有必要存在），因此它们就是子空间的一组基，当然还有其他的基。

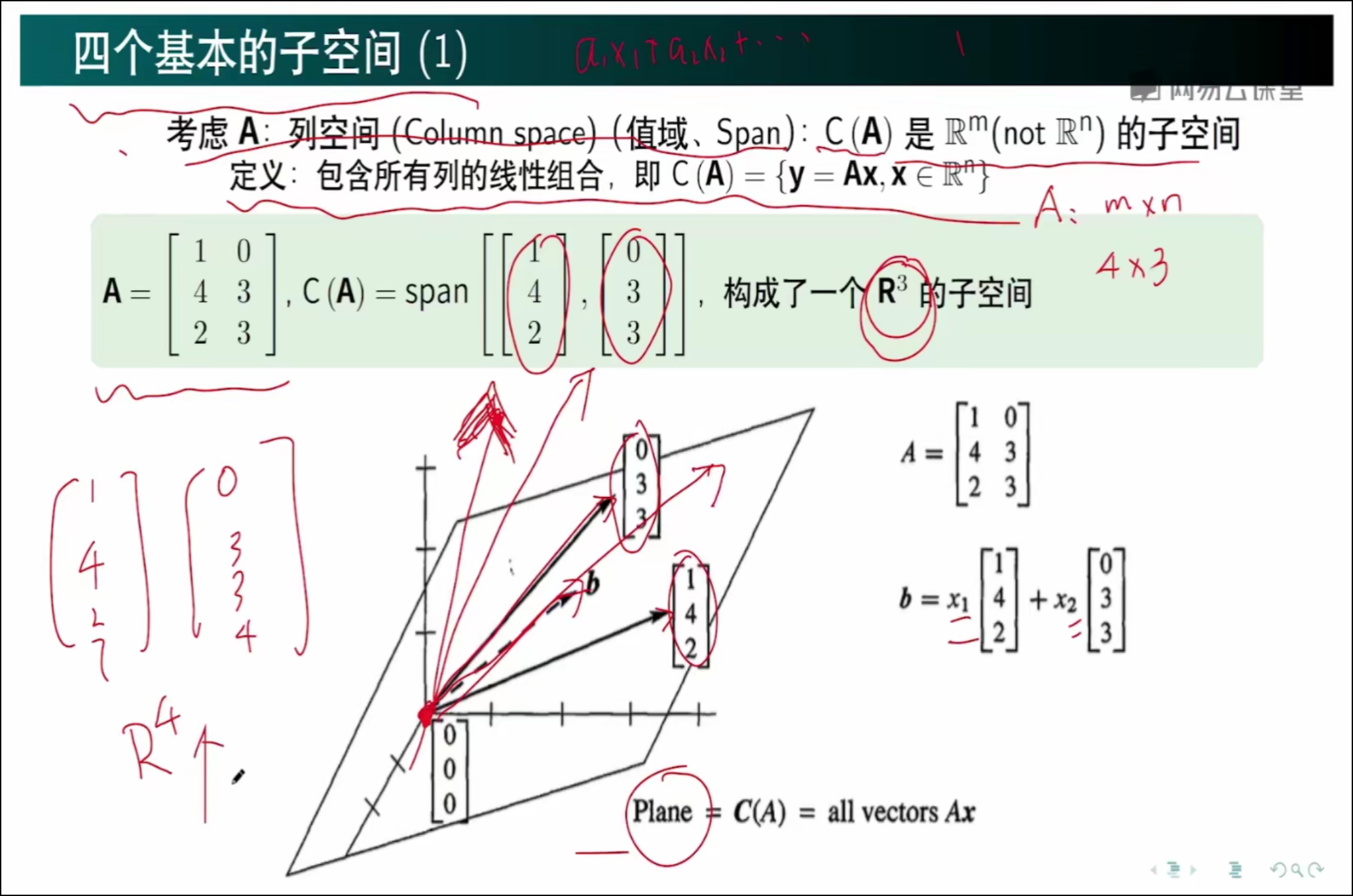
以矩阵A 为例，列向量有3个元素，所以列空间是R3，也就是三维空间，C(A) 是矩阵A 所有的线性组合，因为这两个向量所有的组合只能表示一个平面，所以说C(A) 是R3的一个子空间。

如果矩阵A 存在另一个向量，并且这个向量不与前两个向量组成的平面共面，那么这三个向量就不是线性相关的，因为任意两个向量都不可能线性组合出逃离该子空间的向量。

 

 

 4、特征向量的意义

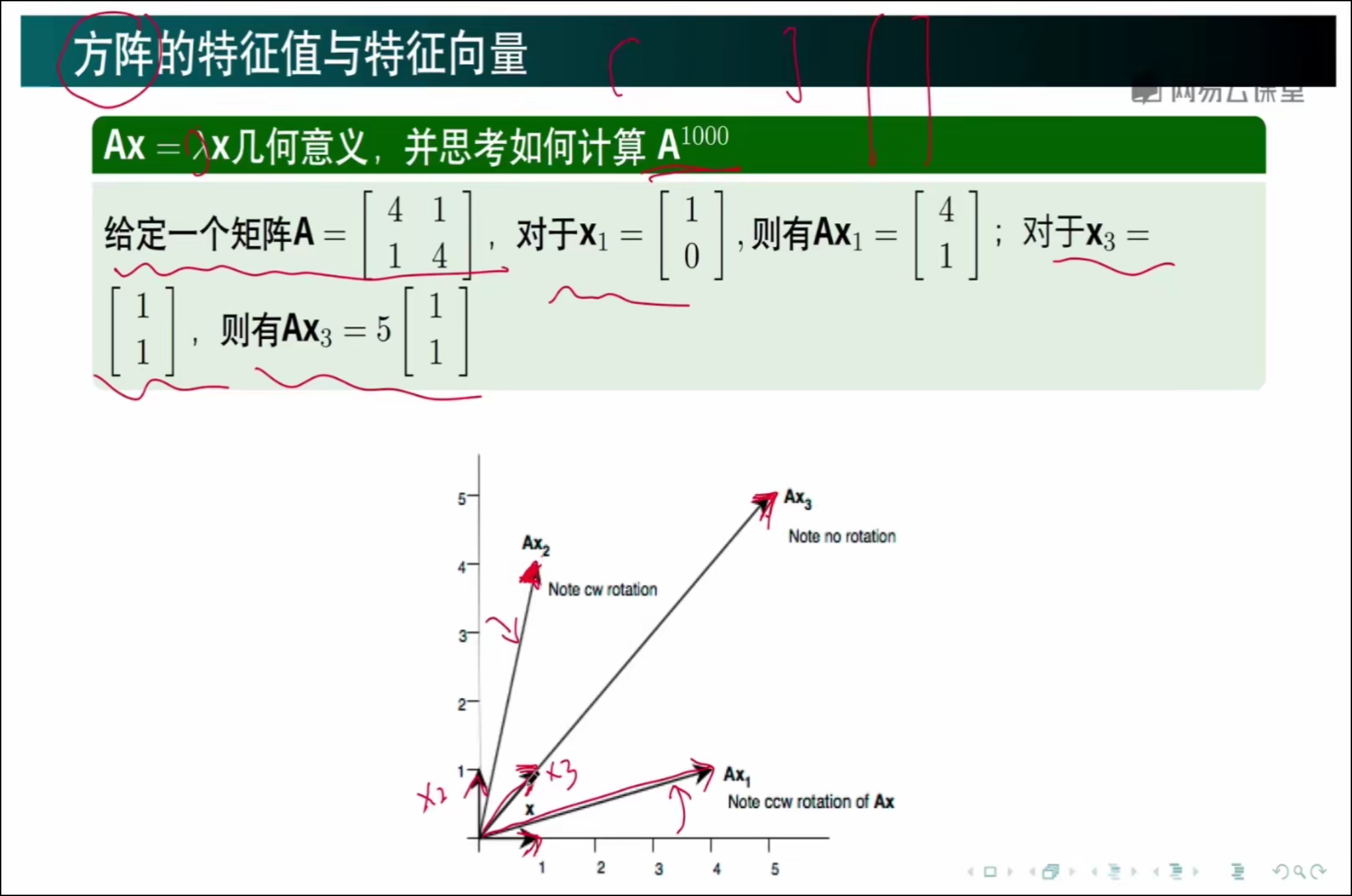
一个矩阵和一个向量相乘，几何意义就是对这个向量，进行旋转+伸缩操作，当没有旋转，或者旋转后的向量和原向量共线，此时的伸缩程度就是特征向量λ

优化问题

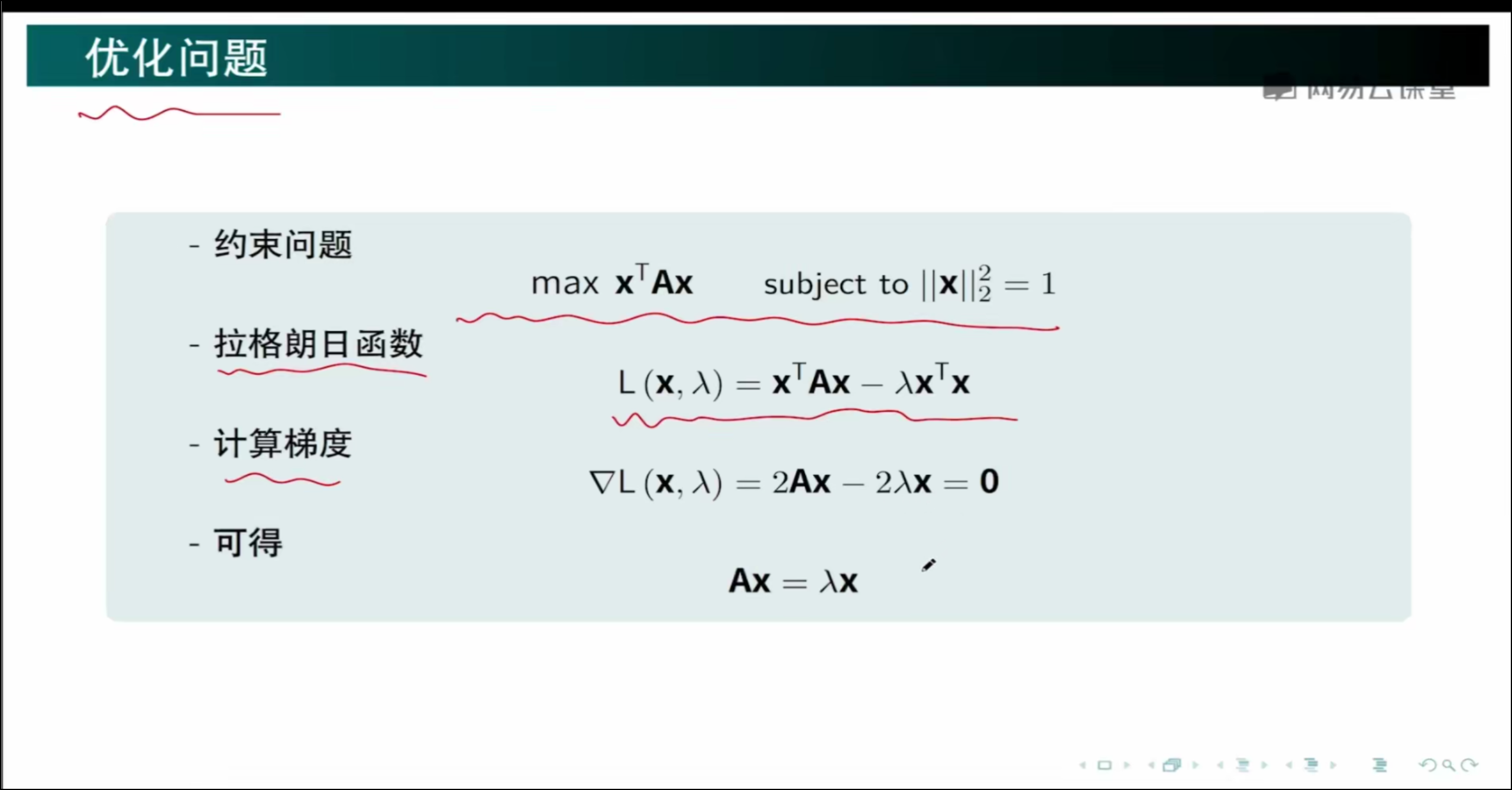
比如影响房价的因素有很多，假设为d个因素，给定样本X=[x1,x2,x3......xn]，则矩阵为d×N，现在是要降维到d`，即d×N → d`×N

因此WT应该是 d`×d 的矩阵，则W ∈ d × d`

降维后 Zn ∈ d`×d × d × 1 = d` × 1

如何找到W

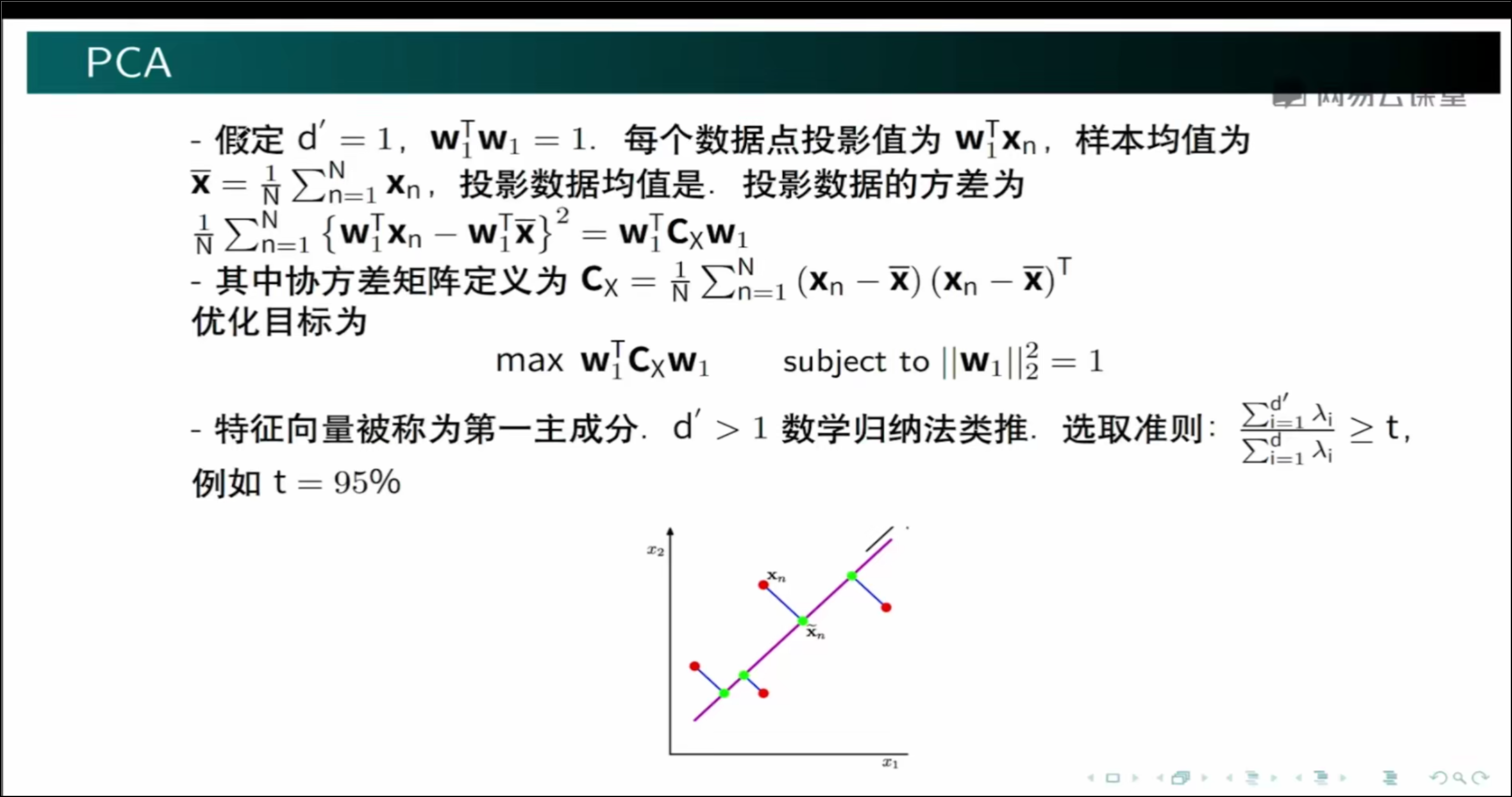
假设原来数据的维度是2，现在要降维到1，就是将平面坐标系中的每个点，投影到X或者Y轴上，就实现了降维。其余类推。