图论分支-Tarjan初步-点双连通分量

上一次我们讲到了边双，这次我们来看点双。

说实话来说，点双比边双稍微复杂一些；

学完边双，我们先看一道题

第一问都不用说了吧，多余的道路，明显的割边。

是不是首先想到用边双，但是我们来看一个图：

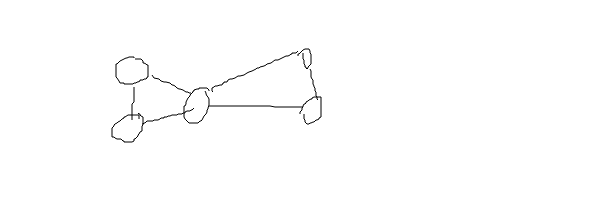
有点丑，但是凑活看吧。

它是一个边双，但是！！！！它竟然没有冲突的边！！！

此时我们就要用点双了（是不是想打死我，竟然没讲，先坑人）

先看概念

都说概念是非常重要的，但是概念似乎有点笼统，可以附图解说

 

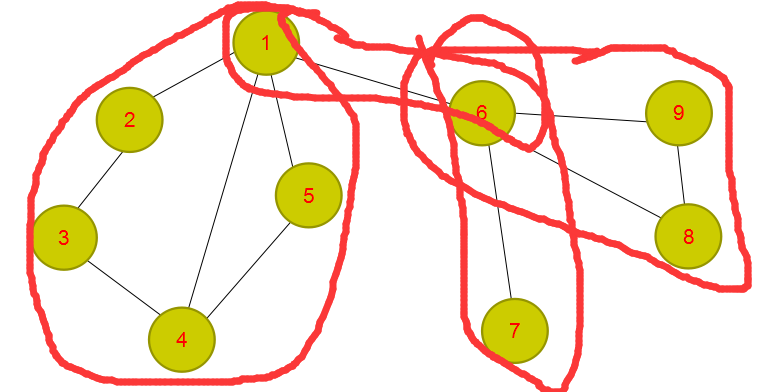
点双的一大特点是它可以重复用点，而那个点就是割点，而我们的缩点操作也是用割点连接各个点双的。

那么我们来看算法，我们在Tarjan时，用栈去维护点双，之后用vector去储存。

我们直接来看上面的题，就会明白这不是点双吗？

然后寻找规律，我们会发现，每一个点双中，只要边个数大于点个数，那么这里的边都是冲突的，那么我们的Code就跃然纸上了

#include<bits/stdc++.h>
#define maxn 10007
#define M 100007
using namespace std;
int n,m,cent=1,t,head[maxn],low[maxn],dfn[maxn],ans1,ans2;
int stackk[maxn],cnt,top,root,cut[maxn],col[maxn],vis[maxn];
int ol;
vector<int >dcc[maxn];
struct node{
    int next,to;
}edge[M*2];

inline void add(int u,int v){
    edge[++cent]=(node){head[u],v};head[u]=cent;
}

void Tarjan(int x,int fa){
    dfn[x]=low[x]=++t;
    stackk[++top]=x;//入栈 
    if(x==root&&head[x]==0){//不联通时的孤立点 
        dcc[++cnt].push_back(x);
        return ;
    }
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(!dfn[y]){
            Tarjan(y,i);
            low[x]=min(low[x],low[y]);//与其他的一样 
            if(low[y]>=dfn[x]){
                if(low[y]>dfn[x]) ans1++;//记录割边个数 
                int z;cnt++;
                do{
                    z=stackk[top--];//从栈中取出 
                    dcc[cnt].push_back(z);//存入 
                }while(z!=y);//停止条件，这个可以想一想为什么 
                dcc[cnt].push_back(x);//把割点也存进去 
            }
        }else if((i^1)!=fa) low[x]=min(low[x],dfn[y]);
    }
}

void clear(){
    ans1=ans2=top=cnt=t=ol=0;cent=1;
    memset(head,0,sizeof head);
    memset(low,0,sizeof low);
    memset(dfn,0,sizeof dfn);
    memset(stackk,0,sizeof stackk);
    memset(dcc,0,sizeof dcc);
    memset(col,0,sizeof col);
    memset(edge,0,sizeof edge);
}

int main(){
//    freopen("way.in","r",stdin);
//    freopen("way.out","w",stdout);
    while(scanf("%d%d",&n,&m)){
        if(n==0&&m==0)break;
        clear();
        int a,b;
        for(int i=1;i<=m;i++){
            scanf("%d%d",&a,&b);
            add(a+1,b+1),add(b+1,a+1);//由于点从零开始，那么我们+1即可 
        }
        for(int i=1;i<=n;i++){
            if(!dfn[i]) root=i,Tarjan(i,-1);
        }
        for(int i=1;i<=cnt;i++,ol=0){
            for(int j=0;j<dcc[i].size();j++){
                vis[dcc[i][j]]=1;//记录点双上的点 
            }
            for(int k=0;k<dcc[i].size();k++){
                for(int j=head[dcc[i][k]];j;j=edge[j].next){
                    if(vis[edge[j].to]) ol++;//ol统计边数 
                }
            }
            if(ol/2>dcc[i].size()) ans2+=ol/2;//由于是双向边，ol会统计量词 
            memset(vis,0,sizeof(vis));
        }
        printf("%d %d\n",ans1,ans2);
    }
}

那么我们就应该懂了一些基本的概念，和简单的操作，那么，留一个彩蛋，我们该如何去缩点连接呢？