图论分支-Tarjan初步-割点和割边
所谓割点(顶)割边,我们引进一个概念
割点:删掉它之后(删掉所有跟它相连的边),图必然会分裂成两个或两个以上的子图。
割边(桥):删掉一条边后,图必然会分裂成两个或两个以上的子图,又称桥。
这样大家就应该能简单理解(怎么可能)割点割边了。
所以我们再来看一个图
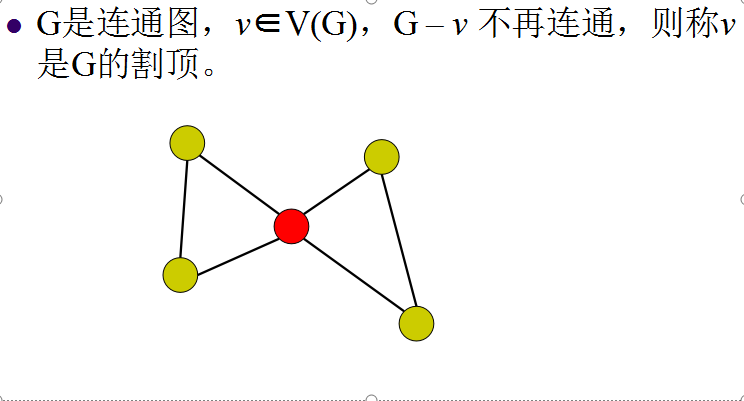
这样大家就能明白了吧(明白是明白了,但是要他干嘛(自动忽略))到后面会明白的。
然后怎么求,这是一个问题,直接想法是搜索,枚举每一个点,然后再去检验是否联通,这样的复杂度应该是O(n2),很显然很不优秀,万一数据是1e5以上不就凉凉了吗。所以我们就可以引进我们的正题了,low-dfn求割点割边。
怎么求?
那么什么是dfn和low呢,简单解释一下,我们的dfn是一个时间戳,也就是访问的时间,而这个就是Tarjan算法的基础(好像忘介绍Tarjan了)而我们的low就是返祖边,也就是通向以前的点的边,所以说,看图。
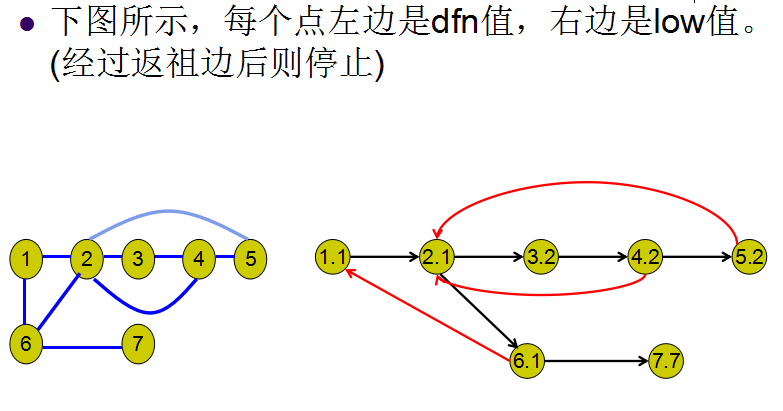
还有一个重要概念也就是,母树继承其子树最小的返祖边,而我们可以观察一下我们的dfn值和low值,再去寻找割点会发现一个重要的事实
每一个割点的dfn一定小于等于其子树的low值,而且如果是root,他的子树大于1他即为割点
这样我们的Code就跃然纸上了
Code
void Tarjan(int x){ low[x]=dfn[x]=++t;//记录时间戳,当然low值一开始也要与dfn值相同 for(int i=head[x];i;i=edge[i].next){//链式前向星 int y=edge[i].to; if(!dfn[y]){//如果没有访问过 Tarjan(y);//搜索查询 low[x]=min(low[x],low[y]);//母树继承子树的最小low值 if(low[y]>=dfn[x]){//发现的规律 flag++;//这个是因为我们的root也有可能是割点,但是它的条件有点苛刻 if(flag>1||x!=root) cut[x]=1;//如果子树分支大于1,那么无论他是什么都是割点了 } }else low[x]=min(low[x],dfn[y]);//返祖边,其连接的点继承最小返祖边连接点的dfn值 } }
备注应该也是很明白了。
然后我们来看割边,上面已经将概念说的很明白了,删边后,图不联通,然后我们根据一个图来理解割边。
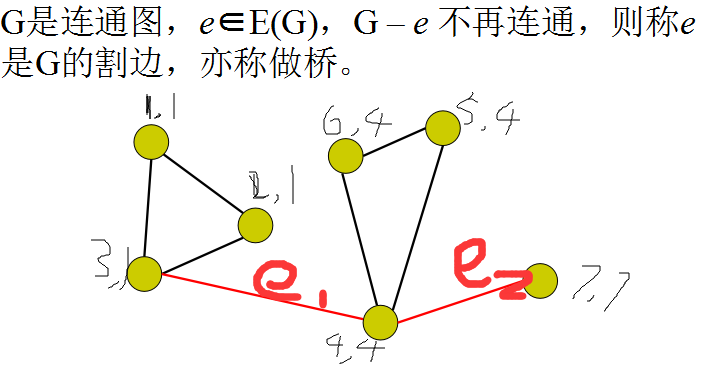
有点丑,左边是dfn,右边是low,红边就是割边,观察一下割边两边两个点的dfn和low值情况,我们会惊喜地发现
母点的dfn值小于(严格小于)子点low值,那么这条边就是割边
好的,我们的代码就出来了
这里引进一道例题

Code
#include<bits/stdc++.h> using namespace std; int n,m,head[100007],cent=1,low[100007],dfn[100007],t,cnt; struct node{ int next,to; }edge[700007]; struct prin{ int u,v; }ans[100007];//记录答案 void add(int u,int v){ edge[++cent]=(node){head[u],v};head[u]=cent; } bool operator <(prin a,prin b){ if(a.u!=b.u) return a.u<b.u; else return a.v<b.v; }//重载运算符 ,sort要用 void Tarjan(int x,int fa){//fa定义的是我们走的上一条边 low[x]=dfn[x]=++t; for(int i=head[x];i;i=edge[i].next){ int y=edge[i].to; if(!dfn[y]){ Tarjan(y,i); low[x]=min(low[x],low[y]); if(low[y]>dfn[x]) { ans[++cnt]=x<y?(prin){x,y}:(prin){y,x};//如果结果成立,那么就可以记录这条边的两个点 } //这里用到了格式转换,prin的定义在上面 }else if((i^1)!=fa){//由于双向建边,需要cent=1,然后用^来验边,或者将fa定义成上一个点 low[x]=min(low[x],dfn[y]);// } } return ; } int main(){ freopen("danger.in","r",stdin); freopen("danger.out","w",stdout); scanf("%d%d",&n,&m); for(int i=1,a,b;i<=m;i++){ scanf("%d%d",&a,&b); if(a==b) continue;//去除自环 add(a,b),add(b,a); } for(int i=1;i<=n;i++){ if(!dfn[i]) Tarjan(i,0);//不连通时Tarjan,一般都是这样写 } sort(ans+1,ans+cnt+1);//题目要求 for(int i=1;i<=cnt;i++){ printf("%d %d\n",ans[i].u,ans[i].v);//输出答案 } return 0; }
这应该就很显然了。
模板讲完了,但还是希望自己的Code要有自己的风格,可以借鉴,但不能照搬。
例题
我们先来看一下割点
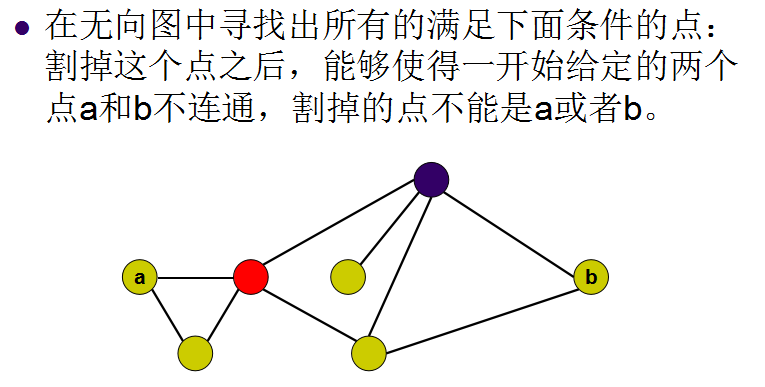
——嗅探器
这个显然是要找割点的,那么怎么找呢?
我们的最大问题是有两个点,在去掉割点后,如何检验他们是否在同一个联通块中?
我们首先的思路是暴力枚举割点,然后检验联通,大概能得10%的分,那么我们来想正解
我们可以以a为根,那么就解决了两个点的问题,但是检验呢?
我们可以将Tarjan定义为bool类型即可,然后在Tarjan的过程中,回溯检验值,详情看代码;
Code
#include<bits/stdc++.h> using namespace std; int n,a,b,head[100007],cent,root,fin,low[100007],dfn[100007]; int t,cut[100007]; struct node{ int next,to; }edge[3000007]; void add(int u,int v){ edge[++cent]=(node){head[u],v};head[u]=cent; } bool Tarjan(int x){ low[x]=dfn[x]=++t; bool f1=(x==fin);// fin是b点,f1是标记 ,检验有没有b点 for(int i=head[x];i;i=edge[i].next){ int y=edge[i].to; if(!dfn[y]){ bool z=Tarjan(y);f1|=z;//回溯标记 low[x]=min(low[x],low[y]); if(low[y]>=dfn[x]&&x!=root&&x!=fin&&z){//这里割点一定不是root cut[x]=1; } }else{ low[x]=min(low[x],dfn[y]); } } return f1;//回溯标记 } int main(){ // freopen("dfnIn.in","r",stdin); // freopen("dfnin.out","w",stdout); scanf("%d",&n); while(scanf("%d%d",&a,&b)&&(a!=0&&b!=0)){ if(a==b) continue; add(a,b),add(b,a); } scanf("%d%d",&root,&fin); Tarjan(root); for(int i=1;i<=n;i++){ if(cut[i]&&low[fin]>=dfn[i]){//检验 printf("%d",i);//输出 return 0; } } printf("No solution"); }
这样就让我们对Tarjan的灵活运用有更深理解。
然后来看割边例题
......
其实上面的板子题就是我们的例题(逃)
好了,Tarjan的割点和割边就结束了。
可以自行找些例题,寻找灵感。


