求解阶乘乘积的最右非零值
整数n的阶乘写作n!,它是从l到n的所有整数的乘积。阶乘增长的速度很快:13!在大多数计算机上不能用32位的整数来存放。70!已经超出多数浮点类型的范围。你的任务是找出n!最右边的非零位。例如,5!=1*2*3*4*5=120,所以5!的最右非零位为2,同样,7!=1*2*3*4*5*6*7=5040,所以7!的最右非零位为4。50!=30414093201713378043612608166064768844377641568960512000000000000,所以最右非零位为2。
写一个程序,计算N(1<=N<=50,000,000)阶乘的最右边的非零位的值。注意:10,000,000!有2499999个零。
输入:一个正整数n。
输出:n!的最右非零位。
函数接口:int factorial(int n);
为表述方便,可以以“尾数”的概念指代最右非零值这一说法。
II.问题分析
对于这么一个问题,恐怕没有人真的把阶乘值算出来,稍大的数据的阶乘值就非常大了。既然是去求最后一位,那么我们可以只运算最后一位,其余数位无须过问。我们可以从数字1开始,依次做乘法运算,遇到零则舍去,然后继续考虑上一个数位。在这种思想下,可以轻松得到一个C语言的算法:
int factorial(int n)
{
int result = 1;
for(int i = 1; i <= n; i++)
{
result *= i;
while(result % 10 == 0)
{
result /= 10;
}
result %= 10;
}
return result;
}
代入数据50检验,得输出为4,这个答案是错误的。跟踪程序的运行并和正确结果做对比,可以发现在运算到数字15的时候首次出现了错误。我们来分析一下。
14!=87178291200
15!= 15*14!=1307674368000
按照我们刚才的分析,在运算到14!之后,我们在程序中保存了一个2,这是14!的最后一位,我们用2乘以15得30,这时再舍弃零,得结果3,但是真实的结果是8。很明显的,12*15和2*15结果是不样的。因此这个算法不正确,之所以会出现错误,是因为最后一位的运算中产生了一个整十,因此要向前一位找到新的非零数,而我们没有保留这一位的全部信息,因此将得到错误的结果。
III.整十进位产生的根源
对于一般的进位(不是整十)我们是不需要特别考虑的,这些进位发生以后,仍然保存着最后一位非零,不会影响我们的运算结果。那么整十进位是怎么产生的呢?
大于十的数计算阶乘的时候,中间就直接夹杂着10这一因子,它可以导致整十进位。所有的因子5同因子2乘起来,也得到10,数字10本身也是5和2的乘积。因此将整个乘式因子分解后,我们可以断定:成对出现的2和5是产生10的根源。单独的2或5和一切其它数字的乘法,都不能产生整十。我们可以先把所有的5*2从乘式中剔除,然后再使用上面提到的第一种算法计算结果就可以了。
然而在乘式中,5的个数和2的个数未必是相等的,实际上除了在1!和0!中两者都不存在因子2和因子5外,在其它乘式中两者数量根本不能相等,后面我们会证明这一点。按照直觉,我们会猜测2更多一点,所以在剔除了等量的因子5和因子2之后,因子5就不存在了,但是因子2还剩下一部分,我们只需要处理剩下的数。但是究竟是谁剩下呢?
IV.5和2,谁更关键?
我们试图确定在M的阶乘中,因子k(素数)到底出现了多少次。实际上,从1到M这些数中,每k个便会有一个k的倍数,这个序列是
k,2k,3k,4k,...
将这些数据中的k提取出去并计数,然后在余下的数据中每k*k个之中又存在k因子,继续提取计数。余下的数据中每k*k*k个数据内又有一个k因子,持续提取计数,直到k*k*...*k大于M。也就是说,M的阶乘中含有因子k的个数可以由以下公式确定:
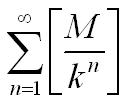
其中用到了取整操作,在程序设计中可以方便的对应为整数的除法。
这样我们可以容易的判断,
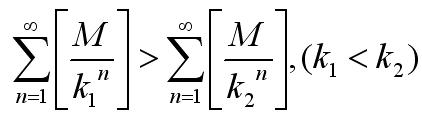
由于5>2因此因子5的个数更少,因子5的个数决定了整十的个数,因此也决定了乘式结尾零的个数。下面我们设计一算法来计算因子5的个数:
/*By Shilyx 2007.9.19,计算对Number!做因子分解后Factor因子的个数并返回*/
int GetFactorNumber(unsigned Number, unsigned Factor)
{
int result = 0;
if(Factor < 2 || Number < 1)
return -1;
while(Number >= Factor)
result += Number /= Factor;
return result;
}
V.计算最右非零位
按照上面的思路,我们现在要着手计算阶乘结果的尾数。对于一个给定的数字M,我们要求得M!中的因子5的个数N,然后从1到M依次处理数据,并在这些数据中除去所有的因子5和N个因子2,然后使用余下的数据按照最开始时提出的算法计算结果。代码及相关分析如下:
/* By Shilyx 2007.9.19,计算Number!的最右非零位并输出*/
int GetLastDigit(unsigned Number)
{
int result = 1;/*这是连乘法的基础值,也是最后要返回的结果*/
int i;/*循环变量*/
int tmp;/*循环中用到的临时值*/
int Count = 0;/*记录找到的因子2的个数,直到和因子5的个数相等*/
int TotalFactors = GetFactorNumber(Number, 5);/*因子5的总数*/
for(i = Number; i >= 1; i--)/*从Number一直向下处理*/
{
tmp = i;
/*尽可能多的得到因子2,直到tmp是个奇数或者不需要更多的因子2*/
while(tmp % 2 == 0 && Count < TotalFactors)
{
tmp /= 2;
Count++;
}
while(tmp % 5 == 0)/*除去所有的因子5*/
tmp /= 5;
tmp %= 10;/*取得个位数*/
result *= tmp;/*做阶乘*/
result %= 10;/*只保留个位数*/
}
return result;/*返回运算结果*/
}
代入数据检验,输出结果完全吻合。
其实不仅仅是最右一位数可以求得,最右任意位数都可以按照上面的方法计算,只是要保留的数据位数不同而已。
VI.更深的探索
上面找到了计算阶乘积最后几位数的一般方法,这个方法对每一个数据都进行了处理,因此,速度上受到了一点限制。考虑阶乘的计算方法细节,我们可以发现一些有用的东西。
(1). 阶乘结果的尾数只能是2,4,8之中的一个(除0!和1!外)
为什么会这样呢?我们可以这样来思考,对于7以下的数字,我们可以非常容易的验证这一点,就不赘述了;对于7及以上数字的阶乘,里面必然包含一个非素因子6,我们可以把阶乘结果表示6A,A是其余数字的乘积,设6A的最后一位数字是k。那么我们考虑6K*6这个数值,且不论这个数值有什么意义,我们先推断一下这个数值的特征。它的尾数是什么呢?6A*6=6*6A,而6*6=36的尾数依然是6,因此6A*6的尾数等同于6A的尾数,也是k。这也就是说,6*k的尾数也是k本身。
在数字1-9中,满足这一条的只有三个数字:2,4,8。
(2).不同数字对阶乘尾数的影响有差异
考虑数字1和6,它们对尾数的变化是没有影响的,尾数与其相乘之后保持不变。
考虑数字9和4,它们对尾数的变化有影响,但是影响是周期性的。尾数同两个9相乘,相当于与1相乘,因为9*9=91;尾数同两个4相乘,相当于与6相乘,因为4*4=16。
考虑数字2,3,7,8,它们对尾数的变化有影响,但是影响也是周期性的。尾数同四个2或者四个8相乘,相当于与6相乘;尾数同四个3或者四个7相乘,相当于与1相乘;
数字0和5无须考虑,所有的5的倍数都已经被完全分解。
根据上面的条件分析,可以得到一个新的思路,这个思路是基于为尾数分布的分析的。比如对尾数9来说,如果阶乘中含有奇数个数字9那么就相当于一个数字9,偶数个数字9相当于一个数字1。
(3).统计尾数的可行性
设法统计到尾数出现的次数,我们的工作会更加轻松。我们现在要确定的是从数字1到N,其间尾数为k的数有多少(k=1..9)。这种分布是以10为周期的,在N和与N接近的一个整十之间,也可能存在以k为尾数的数。那么我们可以根据下面是算法来统计这些数的数目:
/* By Shilyx 2007.9.19,统计1-Number之间的数字中以Digit为尾数的个数*/
int GetLastDigitTimes(unsigned Number, int Digit)
{
if(Number % 10 >= Digit)
return Number / 10 + 1;
return Number / 10;
}
VII.更优的算法
基于以上的分析,我们可以设计一个新的算法,此算法不要求将每个数据处理一次,因此,时间上会有一定的节省。我们现在可以一开始就统计数据吗?还不可以。因为除掉因子5和一部分因子2的工作还没有做,这部分工作我没有找到更好的办法,因此还要使用上面的算法,直到除去了足够多的因子2,然后再使用新算法。对于M的新算法的流程如下:
(1).计算因子5的个数;
(2).从M向1依次处理数据,尽可能多的除去因子2,直到除去的足够多;
(3).从下一个数据开始,使用新算法。计算余下数字中的2,3,4,7,8,9的个数,并分别处理;
(4).分析统计结果,得出最终结果。
算法及其分析如下:
/* By Shilyx 2007.9.19,计算Number的Times次方*/
int Power(int Number, int Times)
{
int result = 1;
while(Times--)
result *= Number;
return result;
}
/* By Shilyx 2007.9.19, 计算Number!的最右非零位并输出方法2*/
int GetLastDigitB(unsigned Number)
{
int result = 1;/*这是连乘法的基础值,也是最后要返回的结果*/
int i;/*循环变量*/
int tmp;/*循环中用到的临时值*/
int Count = 0;/*记录找到的因子2的个数,直到和因子5的个数相等*/
int TotalFactors = GetFactorNumber(Number, 5);/*因子5的总数*/
int T2, T3, T4, T7, T8, T9;/*指示以2,3,4,7,8,9为尾数的个数*/
/*下面依旧是排除因子2的过程*/
for(i = Number; i >= 1; i--)
{
tmp = i;
while(tmp % 2 == 0 && Count < TotalFactors)
{
tmp /= 2;
Count++;
}
while(tmp % 5 == 0)
tmp /= 5;
tmp %= 10;
result *= tmp;
result %= 10;
if(Count == TotalFactors && i % 5 == 1)
break;
}
i--;
/*因子2排除完毕,开始使用新方法统计各尾数出现次数并对自身的周期取模*/
T2 = GetLastDigitTimes(i, 2) % 4;
T3 = GetLastDigitTimes(i, 3) % 4;
T4 = GetLastDigitTimes(i, 4) % 2;
T7 = GetLastDigitTimes(i, 7) % 4;
T8 = GetLastDigitTimes(i, 8) % 4;
T9 = GetLastDigitTimes(i, 9) % 2;
/*处理余下数据中的所有因子5*/
for(; i >= 1; i -= 5)
{
tmp = i;
while(tmp % 5 == 0)
tmp /= 5;
tmp %= 10;
result *= tmp;
result %= 10;
}
/*处理得到的不同尾数的出现次数*/
result *= Power(2, T2);
result *= Power(3, T3);
result *= Power(4, T4);
result %= 10;
result *= Power(7, T7);
result %= 10;
result *= Power(8, T8);
result %= 10;
result *= Power(9, T9);
result %= 10;
return result;
}
这个新的算法在很大程度上减小了循环体的长度,如果能找到更好的处理因子2的办法,那么算法还可以更优。
VIII.两种算法的比较
主要是从运行时间是比较两种算法,在Number值较小的情况下,不好判断哪一个速度更快,我们计算一亿的阶乘的尾数,并使用Windows提供的GetTickCount函数来标志运行时间,在我的机器上前一个算法耗费时间是10484,新的算法则是5016,由此可见,新的算法在大量数据处理上可以节约大约一半的时间。
正如文中所说,如果有更好的剔除因子2的算法,那么运算速度还可以得到进一步改进。如果各位朋友有新的想法,可以在此留言,也可以给我发邮件我的邮箱是OverSleep@163.com,QQ是303013274,欢迎交流,By Shilyx。
IX.再一次更优的算法(2007.9.25,中秋)
就在第二天,我找到了前面提到的更好的算法,利用上面的时间测试方法对新方法测试,结果是零,可见新算法的威力!我试过运算很大的无符号整数到40亿,几乎不耗费什么时间,瞬间输出结果。
下面贴出代码:
int GetLastDigitTimesDiv5(unsigned Number, int Digit)
{
if(Number < Digit)
return 0;
if(Number % 10 >= Digit)
return Number / 10 + 1 + GetLastDigitTimesDiv5(Number / 5, Digit);
return Number / 10 + GetLastDigitTimesDiv5(Number / 5, Digit);
}
int GetLastDigitC(unsigned Number)
int result = 1, i, tmp, Count = 0;
int TotalFactors = GetFactorNumber(Number, 5);
int T2, T3, T4, T42, T7, T8, T84, T842, T9;
if(Number > 6) //为了排除6的影响,先乘一个
result = 6;
T2 = GetLastDigitTimesDiv5(Number, 2);
T3 = GetLastDigitTimesDiv5(Number, 3);
T4 = GetLastDigitTimesDiv5(Number, 4);
T7 = GetLastDigitTimesDiv5(Number, 7);
T8 = GetLastDigitTimesDiv5(Number, 8);
T9 = GetLastDigitTimesDiv5(Number, 9);
T84 = 0; //对尾数为8的数排2后的尾数为4的个数
T42 = 0; //对尾数为4的数排2后的尾数为2的个数
T842 = 0; //对所有T84的数排2后的尾数为2的个数
if(TotalFactors > 0) //处理T8
{
if(T8 >= TotalFactors) //对T8做一次排2已足够
{
T8 -= TotalFactors; //剩余的T8
T9 += TotalFactors / 2; //新生成的T9
T4 += TotalFactors - TotalFactors / 2; //新生成的T4
TotalFactors = 0; //不继续需要排2
}
else //T8不够用
{
TotalFactors -= T8; //对所有的T8排2
T9 += T8 / 2; //新生成的T9
T84 = T8 - T8 / 2; //新生成的T84
T8 = 0; //没有T8了
if(T84 >= TotalFactors) //对T84做一次排2已足够
{
T84 -= TotalFactors; //剩余的T84
T7 += TotalFactors / 2; //新生成的T7
T2 += TotalFactors - TotalFactors / 2; //新生成的T2
TotalFactors = 0; //不继续需要排2
}
else //T84不够用
{
TotalFactors -= T84; //对所有的T84排2
T7 += T84 / 2; //新生成的T7
T842 = T84 - T84 / 2; //新生成的T842
T84 = 0; //没有T84了
if(T842 >= TotalFactors) //对T842做一次排2已足够
{
T842 -= TotalFactors; //剩余的T842
TotalFactors = 0; //不继续需要排2
}
}
}
}
if(TotalFactors > 0) //处理T4
{
if(T4 >= TotalFactors) //对T4做一次排2已足够
{
T4 -= TotalFactors; //剩余的T4
T7 += TotalFactors / 2; //新生成的T7
T2 += TotalFactors - TotalFactors / 2; //新生成的T2
TotalFactors = 0; //不继续需要排2
}
else //T4不够用
{
TotalFactors -= T4; //对所有的T4排2
T7 += T4 / 2; //新生成的T7
T42 = T4 - T4 / 2; //新生成的T42
T4 = 0; //没有T4了
if(T42 >= TotalFactors) //对T42做一次排2已足够
{
T42 -= TotalFactors; //剩余的T42
TotalFactors = 0; //不继续需要排2
}
}
}
if(TotalFactors > 0) //处理T2
{
if(T2 >= TotalFactors) //对T2做一次排2已足够
{
T2 -= TotalFactors;
TotalFactors = 0;
}
}
T2 %= 4; //处理计算得到的位数
T42 %= 4;
T842 %= 4;
T3 %= 4;
T4 %= 2;
T84 %= 2;
T7 %= 4;
T8 %= 4;
T9 %= 2;
result *= Power(2, T2);
result %= 10;
result *= Power(2, T42);
result %= 10;
result *= Power(2, T842);
result %= 10;
result *= Power(3, T3);
result *= Power(4, T4);
result %= 10;
result *= Power(4, T84);
result %= 10;
result *= Power(7, T7);
result %= 10;
result *= Power(8, T8);
result %= 10;
result *= Power(9, T9);
result %= 10;
return result;
}
下面是算法说明
如果用 C 表示 [n/5] + [n/25] + [n/125] + ..., 那么需要求的是下面的同余方程
n ! ≡ x * 10^c (mod 10^(c+1))
的解 x , 0< x ≤ 9.
上面这个同余方程等价于下面的方程组
n! ≡ x * 5^c * 2^c (mod 2^(c+1)), n! ≡ x * 2^c * 5^c (mod 5^(c+1))
当 n > 1 时所有的偶数都是上面的方程组中第一个方程的解,而且, n > 1 时该方程组的
第一个方程没有奇数解,因此 n > 1 时只需要考虑下面这个方程(即方程组的第二个方程)
的符合 0 < x <9 的偶数解:
n! ≡ x * 2^c * 5^c (mod 5^(c+1)). (a)
用 h(n) 表示 所有与 5 互素且不大于 n 的正整数的连乘积, 则 n! 可以表为
h(n) * 5^[n/5] * h([n/5]) * 5^[n/25] * h([n/25]) * 5^[n/125] * h([n/125]) *... ,
代入 (a) 式,消去 5 的乘方后得到下面的同余方程
h(n) * h([n/5]) * h([n/25]) * ... ≡ x * 2^c (mod 5), (b)
由于 3 * 2 ≡ 1 (mod5), 因此 (b) 式变为
3^c * h(n) * h([n/5]) * h([n/25]) * ...≡ x (mod5), (c)
由 Euler-Fermat 公式知( % 表示求模运算 )
3^c ≡ 3 ^ (c % 4) (mod 5),
由 Wilson 定理有
h(n) ≡ (-1)^([n/5]) * (( n % 5 )! ) (mod 5),
把上面两式代入 (c) 就得到了
3^(c%4) * (-1)^c * ( n % 5 )! * ([n/5] % 5)! * ([n/25] % 5)!*...
≡ x (mod 5) (d)
由 c 的表达式可知, 我们可以在求 [n/5],[n/25],[n/125],... 的过程中
求出 c 和 (n % 5)!,([n/5] % 5)!,([n/25] % 5)!,..., 这样就可以求得
(d) 式的左边.把最后的结果 模 5 后即可以求得 x.
这个过程实际上是用连除法求 n 的 5 进制表示. 由于 5 进制表示的 各个 位上的数字是任意的,因此 (d) 式的 左边 已不能再简化.由于任意 求进制表示的 方法本质上都是连除法,因此这个算法 本质上 已是最优算法..
这是一个时间复杂度 O(log n) 的算法
用 C 语言写的该算法的实现
为了确保跨平台性,我使用了
C 99 规定的类型 uint_fast32_t, 为使用这个类型,请 包含 c 语言的 标准头文件 stdint.h. 下面是我的函数
uint_fast32_t GetRightestNoZeroDigitA(uint_fast32_t n)
{
uint_fast32_t m = 1, c = 0, i;
uint_fast32_t cr[] = { 1, 3, 4, 2 };
uint_fast32_t rr[] = { 1, 6, 2, 8, 4 };
while( n > 1){
if ( 2 == (i = n % 5) )
m <<= 1;
else if ( 4 == i )
m <<= 2;
c += n /= 5;
}
if ( c & 1 )
return rr[ ( cr[ c % 4 ] * 4 * m ) % 5 ];
return rr[ ( cr[ c % 4 ] * m ) % 5 ];
}
转自:http://hi.baidu.com/shilyx/blog/item/5bb7733e6313ec3e70cf6cd9.html
http://hi.baidu.com/tianyuan006/blog/item/5c7c7bfaa5d5baddb48f3196.html






