常见的激活函数、损失函数、优化器(未完待续)
学习笔记,持续更新修订中.......
1.激活函数
个人觉得关于激活函数需要思考5个问题:
1.为什么要使用激活函数?(不完全理解)
如果不用激励函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
2.该激活函数的效果是什么?(也就是如何对输入进行调整的)
3.该激活函数有什么优缺点?
4.在哪些步骤里需要添加激活函数?
5.如何选择激活函数?
1.1 sigmoid
sigmoid函数可以将实数映射到(0, 1)区间内,平滑、易于求导。其公式如下:


测试如下:

import torch import torch.nn as nn import matplotlib.pyplot as plt import numpy as np x = np.arange(-10, 10, 0.1) y1= nn.Sigmoid()(torch.tensor(x,dtype=torch.float)) y2= 1/(1.0+np.exp(0-x))# 1/(1+e(-x)) plt.plot(x, y1, label="sigmoid",color='b') plt.plot(x, y2, label="sigmoid",color='r') plt.xlabel("x") plt.ylabel("y") # plt.ylim(0, 1) plt.legend() plt.show()
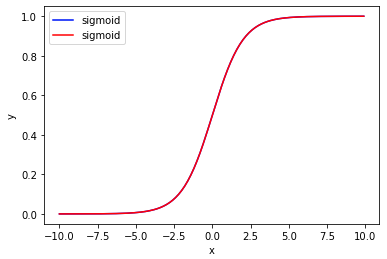
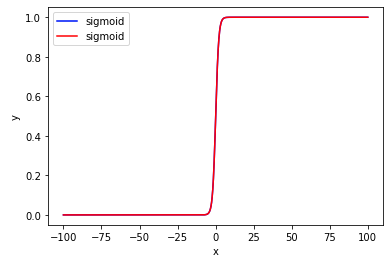
但同时也容易出现问题,就是当输入范围(x)较大时,Sigmoid的输出大都分布在0和1(如上右图),使得数值本身的差异变小。比如输入0、25、100,经过Sigmoid后的值分别为0.5、1、1(近似),原值间100与0的差异明显大于25与0,但经过Sigmoid后差异几乎消失了。
优点与不足(来源自August-us的博客):
1.反向传播的计算比较简单,根据公式可快速计算出反向传播的导函数。
2.但该函数的计算本身就有点不容易,要计算指数还要计算除法。
3.此外,该函数还具有软饱和性,训练的时候,对于绝对值较大的数,计算出来的梯度非常小,如果多层的梯度相乘,导致计算出来的最终梯度非常小,使得参数几乎无法更新,训练无法正常进行下去,这就是所谓的梯度消失问题。
1.2 Tanh (双曲正切激活函数)
Tanh激活函数公式如下:

测试如下:

# tanh=(e(x)-e(-x))/(e(x)+e(-x)) import torch import torch.nn as nn import matplotlib.pyplot as plt import numpy as np x = np.arange(-10, 10, 0.1) y1= nn.Tanh()(torch.tensor(x,dtype=torch.float)) y2= (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(0-x)) plt.plot(x, y1, label="tanh by pytorch",color='b') plt.plot(x, y2, label="tanh by numpy",color='r') plt.xlabel("x") plt.ylabel("y") # plt.ylim(0, 1) plt.legend() plt.show()

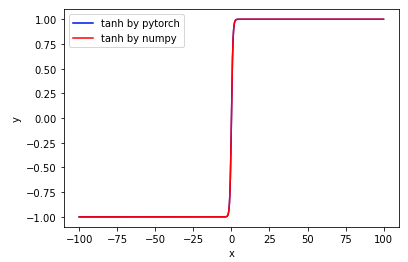
从上图可见,其与Sigmoid激活函数相似,就是当输入范围(x)较大时,Tanh的输出也大都分布在0和1(如上右图)。 只是Tanh将输出对称到0上了,即tanh(x)=2*sigmoid(2x)-1
优点与不足:
其优缺点与Sigmoid相近,但博主说:解决了sigmoid函数收敛变慢的问题,相对于sigmoid提高了收敛速度。(还未理解)
1.3 ReLU
ReLU激活函数公式如下:

简单的测试

# relu=max(0,x) import torch import torch.nn as nn import matplotlib.pyplot as plt import numpy as np x = np.arange(-10, 10, 0.1) y1= nn.ReLU()(torch.tensor(x,dtype=torch.float)) y2=[] for itm in x: y2.append(max(0,itm)) y2=np.array(y2) plt.plot(x, y1, label="relu by pytorch",color='b') plt.plot(x, y2, label="relu by numpy",color='r') plt.xlabel("x") plt.ylabel("y") # plt.ylim(0, 1) plt.legend() plt.show()
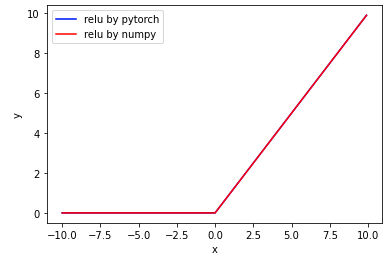

优点与不足(来源自August-us的博客)
1.该函数非常简单,对深度学习性能的提升非常大,ReLU的收敛速度要远远快于Sigmoid和Tanh。
2.x>0的时候,函数的导数为1,不存在梯度衰减的问题。虽然ReLU函数缓解了梯度消失的问题,但是同时也带来了梯度死亡问题。在x<0的时候,函数是硬饱和的,这个时候导数直接为0了,一旦输入落进这个区域,那么神经元就不会更新权重了,这个现象称为神经元死亡。稍微值得欣慰的一点就是通过良好的初始化和学习率设置可以使得神经元死亡的概率不那么大。
3.可以产生稀疏性,可以看到小于0的部分直接设置为0,这就使得神经网络的中间输出是稀疏的,有一定的Droupout的作用,也就能够在一定程度上防止过拟合。
1.4 Softmax
softmax的公式如下:
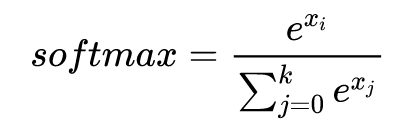
与Sigmoid、Tanh、ReLU不同,softmax是针对多分类问题,也就是输出是每一个类别的概率,且所有类别的概率和为1。
疑惑:
Q: 在Pytorch中存在torch.nn.functional.log_softmax()和 torch.nn.functionalsoftmax(),这两者的区别,为何会有log_softmax的存在?
A: log_softmax是在softmax的结果上再做多一次log运算?知乎答主的回答说的比较合理。对softmax进行log处理是为了解决溢出问题,当i很大时,e(xi)会溢出float的上限。因此,尽管在数学表示式上是对softmax的结果取对数,但是在实操中过程却不是这样简单,实操如下。


import torch import torch.nn.functional as F import torch.nn as nn target = torch.tensor([1,0]) x=torch.randn((2,3)) sm=nn.Softmax(dim=1)(x) sm_lg1=torch.log(sm) sm_lg2=torch.nn.functional.log_softmax(x,dim=1) print(f'original tensor:......\n{x}\n') print('1.softmax vs. log_softmax') print(f'softmax:......\n{sm}\n') print(f'softmax and log:.....\n{sm_lg1}\n') print(f'log_softmax:......\n{sm_lg2}\n')
结果如下:

2.损失函数
2.1交叉熵
见缝插针:
Q: Pytorch中nn.CrossEntropyLoss()与nn.NLLLoss()的差异
A: CrossEntropyLoss 本来应该只是计算cross entropy的,然而实际上它里面还包括自动计算一次softmax。nn.CrossEntropyLoss()是nn.logSoftmax()和nn.NLLLoss()的整合,可以直接使用它来替换网络中的这两个操作。使用CrossEntropyLoss时不能先做softmax处理。

import torch import torch.nn.functional as F import torch.nn as nn target = torch.tensor([1,0]) x=torch.randn((2,3)) sm=nn.Softmax(dim=1)(x) sm_lg1=torch.log(sm) sm_lg2=torch.nn.functional.log_softmax(x,dim=1) print(f'original tensor:......\n{x}\n') print('1.softmax vs. log_softmax') print(f'softmax:......\n{sm}\n') print(f'softmax and log:.....\n{sm_lg1}\n') print(f'log_softmax:......\n{sm_lg2}\n') loss_2=nn.NLLLoss()(sm_lg1,target) loss_3=nn.CrossEntropyLoss()(x, target) print('2.NLLLoss vs. CrossEntropyLoss') print(f'loss by NLLLoss:{loss_2}') print(f'loss by CrossEntropyLoss:{loss_3}')
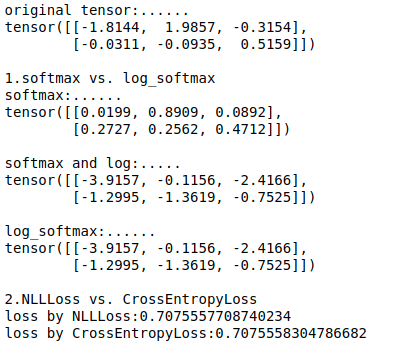
结果如下:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号