混淆矩阵及相关精度指标计算和实现记录

学习笔记，持续更新修订中.......

1.混淆矩阵

（1）常见二分类混淆矩阵如下：

混淆矩阵		预测值
		正	负
真实值	正	TP	FN
	负	FP	TN

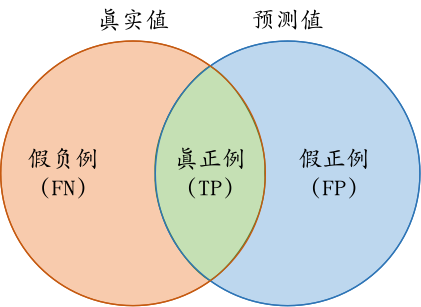
True Positive：真正类(TP)，样本的真实类别是正类，并且模型预测的结果也是正类。

False Negative：假负类(FN)，样本的真实类别是正类，但是模型将其预测成为负类。（统计学上的第二类误差（Type II Error））

False Positive：假正类(FP)，样本的真实类别是负类，但是模型将其预测成为正类。（统计学上的第一类误差（Type I Error））

True Negative：真负类(TN)，样本的真实类别是负类，并且模型将其预测成为负类。

（2）类别为3，每类分别记为A，B，C

混淆矩阵		预测值
		A	B	C
真实值	A	AA	AB	AC
	B	BA	BB	BC
	C	CA	CB	CC

2.精度指标

2.1 Overall Accuracy、Average Accuracy

2.1.1 定义及计算方式

以上述二分类为例：

#1.总体精度(Overall Accuracy, OA)：样本中正确分类的总数除以样本总数。
OA=(TP+TN)/(TP+FN+FP+TN)
#2.平均精度(Average Accuracy, AA)：每一类别中预测正确的数目除以该类总数，记为该类的精度，最后求每类精度的平均。
AA=(TP/(TP+FN)+TN/(FP+TN))/2

2.1.2 指示意义

OA与Accuracy定义一致。AA与Recall计算公式比较一致，不过考虑了正负两例的计算。

2.2 Accuracy、Precision、Recall以及F-score

一般针对二分类，有正负例区分。

2.2.1 定义及计算方式

#1.准确率(Accuracy)：模型的精度，即模型预测正确的个数 / 样本的总个数;一般情况下，模型的精度越高，说明模型的效果越好。
Accuracy=(TP+TN)/(TP+TN+FP+FN) 
#2.精确率(Precision)：模型预测为正的部分的正确率。
Precision=TP/(TP+FP) 
#3.召回率(Recall)：真实值为正的部分，被模型预测出来且正确的比重。
Recall=TP/(TP+FN) 
#4.F1-score：此指标综合了Precision与Recall的产出的结果，取值范围从0到1的，1代表模型的输出最好，0代表模型的输出结果最差。
F=2*Precision*Recall/(Precision+Recall)

2.2.2 指示意义 

总体上来说，我们希望这些值尽可能大。但实际上却不能尽如人意，而且每个指标的指示意义各不相同，需要参照定义、具体样本和预测预期进行分析；

2.3 IoU与MIoU

2.3.1 定义与计算

以二分类为例：

IoU(Intersection over Union，交并比)：计算某一类别预测结果和真实值的交集和并集的比值。计算公式如下：

     

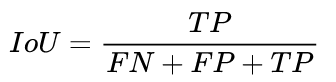
MIoU(Mean Intersection over Union，平均交并比)：计算所有类别的IoU的平均值。计算公式如下（因k从0开始，故需要加1）：

    

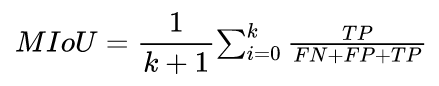
# 计算1中二分类混淆矩阵中正负两类的MIoU
MIoU=(IoU(正)+IoU(负))/2
    =(TP/(FN+FP+TP)+TN/(TN+FN+FP))/2

更一般的，多分类：

某一类的IoU的分子为：该类所在混淆矩阵对角线的值。

某一类的IoU的分母为：该类所在混淆矩阵对角线的位置对应的行和列的总和。（对角线位置的值只能计算一次）

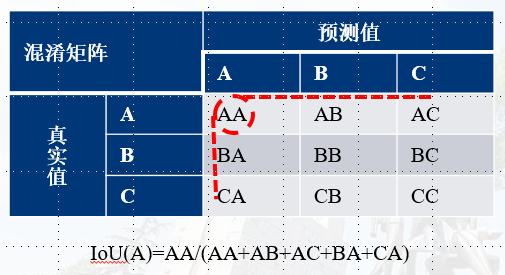
2.3.2 指示意义

因对于一个样本来说，FN+TP是固定的，那么IoU就可以变为IoU=TP/(K+FP)，那么主要相当于分析TP与FP的变化趋势。孤立的分析IoU，这里有4种情况可能使得IoU变大：

1）TP不变，FP减小；IoU肯定变大

2）TP变小，FP变小；IoU应该可大可小

3）TP变大，FP不变；IoU肯定变大

3）TP变大，FP变大；IoU应该可大可小！如下表格C1到C2，I_C1=1/(1+5)=1/6、I_C2=3/(4+5)=1/3；此时虽然IoU变大，但是Accuracy却变小了，模型的好坏需要另外讨论。

假设	TP	FN	FP	TN	Total
C1	1	4	1	4	10
C2	3	2	4	1	10
C3	2	3	2	3	10

也就是说IoU变大，模型不一定变好，但大多数情况下还是变好的。　

2.4 Kappa系数

2.4.1 定义及计算

Kappa系数用于一致性检验，也可以用于衡量分类精度，其计算是基于混淆矩阵的。公式如下：

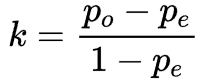
 其中，p_o是每一类正确分类的样本数量之和除以总样本数，也就是总体分类精度（OA）；p_e为每一类真实数量乘以该类预测数量的总和除以所有类别总数的平方，如下：

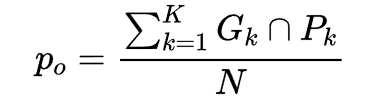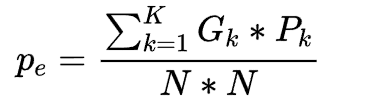，其中G_k为第k类的真实标签数量，P_k为第k类的预测标签数量，K为总的类别数量，N为所有类别标签的总数。

 在上述二分类混淆矩阵中，p_o，p_e为：

，

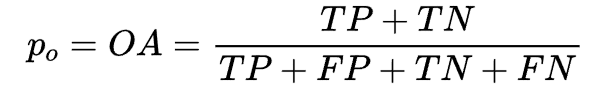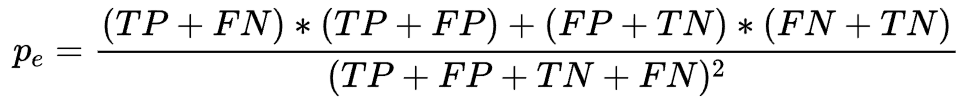
2.4.2 指示意义

kappa计算结果为-1~1，但通常kappa是落在 0~1 间，可分为五组来表示不同级别的一致性（真实值与预测值）：0.0~0.20极低的一致性(slight)、0.21~0.40一般的一致性(fair)、0.41~0.60 中等的一致性(moderate)、0.61~0.80 高度的一致性(substantial)和0.81~1几乎完全一致(almost perfect)。

Kappa范围	指示意义
0.00~0.20	一致性极低
0.21~0.40	一致性一般
0.41~0.60	一致性中等
0.61~0.80	一致性高度
0.81~1.00	几乎完全一致

 3.代码实现

scikit-learn中集成了较为全面的精度指标计算，方便快捷（推荐）。

便于熟悉个指标计算，使用Python进行简单的实现（粗略检查，可能存在问题），分为二分类和多分类版本：

import numpy as np
def computeAccuracyIndex2BinaryClassification(gt,pd,nclass,decimal_digits=4,verbose=True):
    assert gt.shape[0]==pd.shape[0]
    N=gt.shape[0]
    '''confusion matrix'''
    cmat=np.zeros((nclass,nclass)) # confusion matrix
    for i in range(nclass):
        for j in range(nclass):
            tmp= np.sum((gt==i)&(pd==j))
            cmat[i][j]=tmp
    '''OA、AA'''   
    OA=np.sum(np.diagonal(cmat))/np.sum(cmat) # equal to OA
    AA=np.mean(np.diagonal(cmat)/np.sum(cmat,axis=1)) # 求和维度
    '''Accuracy、Precision、Recall、F'''
    Accuracy=OA
    Precision=cmat[1,1]/np.sum(cmat[1,:])
    Recall=cmat[1,1]/np.sum(cmat[:,1])
    F=2*Precision*Recall/(Precision+Recall)
    '''IoU、MIoU'''
    MIoU=0
    IoU=np.zeros(nclass)
    for i in range(nclass):
        IoU[i]=cmat[i,i]/(np.sum(cmat[i,:])+np.sum(cmat[:,i])-cmat[i,i])
    MIoU=np.mean(IoU)
    '''Kappa'''
    po=OA
    pe=0
    for i in range(nclass):
         pe+=(np.sum(cmat[i,:])*np.sum(cmat[:,i]))
    pe=pe/(N*N)
    Kappa=(po-pe)/(1-pe)

    if decimal_digits is not None:
        OA=np.around(OA,decimal_digits)
        AA=np.around(AA,decimal_digits)
        Accuracy=np.around(Accuracy,decimal_digits)
        Precision=np.around(Precision,decimal_digits)
        Recall=np.around(Recall,decimal_digits)
        F=np.around(F,decimal_digits)

        IoU=np.around(IoU,decimal_digits)
        MIoU=np.around(MIoU,decimal_digits)
        Kappa=np.around(Kappa,decimal_digits)
    if verbose:
        print(f'confusion matrix:\n {cmat}')
        print(f'Index 1: OA={OA} AA={AA}')
        print(f'Index 2: Accuray={Accuracy} Precision={Precision} Recall={Recall} F={F}') # 此体系一般针对二分类,且1对应正例
        print(f'Index 3: MIoU={MIoU} IoU={IoU}')
        print(f'Index 4: Kappa={Kappa}')

    return [OA,AA],[Accuracy,Precision,Recall,F],[MIoU,IoU],[Kappa]

# 测试
gt=np.array([0, 1, 0, 0])
pd=np.array([0, 1, 0, 1])
nclass=2
decimal_digits=4
computeAccuracyIndex2BinaryClassification(gt,pd,nclass,4,True)

import numpy as np
def computeAccuracyIndex2MultiClassification(gt,pd,nclass,decimal_digits=4,verbose=True):
    assert gt.shape[0]==pd.shape[0]
    N=gt.shape[0]

    '''confusion matrix'''
    cmat=np.zeros((nclass,nclass)) # confusion matrix
    for i in range(nclass):
        for j in range(nclass):
            tmp= np.sum((gt==i)&(pd==j))
            cmat[i][j]=tmp
    '''OA、AA'''   
    OA=np.sum(np.diagonal(cmat))/np.sum(cmat) # equal to OA
    AA=np.mean(np.diagonal(cmat)/np.sum(cmat,axis=1)) # 求和维度

    '''IoU、MIoU'''
    MIoU=0
    IoU=np.zeros(nclass)
    for i in range(nclass):
        IoU[i]=cmat[i,i]/(np.sum(cmat[i,:])+np.sum(cmat[:,i])-cmat[i,i])
    MIoU=np.mean(IoU)
    '''Kappa'''
    po=OA
    pe=0
    for i in range(nclass):
         pe+=(np.sum(cmat[i,:])*np.sum(cmat[:,i]))
    pe=pe/(N*N)
    Kappa=(po-pe)/(1-pe)

    if decimal_digits is not None:
        OA=np.around(OA,decimal_digits)
        AA=np.around(AA,decimal_digits)
        IoU=np.around(IoU,decimal_digits)
        MIoU=np.around(MIoU,decimal_digits)
        Kappa=np.around(Kappa,decimal_digits)
    if verbose:
        print(f'confusion matrix:\n {cmat}')
        print(f'Index 1: OA={OA} AA={AA}')
        print(f'Index 2: MIoU={MIoU} IoU={IoU}')
        print(f'Index 3: Kappa={Kappa}')

    return [OA,AA],[MIoU,IoU],[Kappa]
gt=np.array([2, 0, 2, 2, 0, 1])
pd=np.array([0, 0, 2, 2, 0, 2])
nclass=3
decimal_digits=4
computeAccuracyIndex2MultiClassification(gt,pd,nclass,4,True)