2018.8.20提高AB组模拟考试

还是来填坑了...

 

T1 题意简述：jzoj4421

 

Description

SillyHook要给小朋友出题了，他想，对于初学者，第一题肯定是a+b 啊，但当他出完数据后神奇地发现.in不见了，只留下了一些.out，他想还原.in，但情况实在太多了，于是他想要使得[a,b] ([a,b] 表示a,b 的最小公倍数)尽可能大。

Input

输入文件的第一行一个整数T 表示数据组数。
接下来T行每行一个整数n ，表示.out中的数值，即a+b=n 。

Output

共T行，每行一个整数表示最大的[a,b] 的值。

Data Constraint

 30%的数据满足 T<=10,n<=1000
100% 的数据满足T<=10000 ,n<=10^9

 

   解题思路：打表找规律。

             先暴力枚举下，发现答案分3种情况：

             1.n是奇数：a=floor(n/2),b=ceil(n/2)。

             2.n是偶数且n/2是偶数：a=n/2-1,b=n/2+1。

             3.n是偶数且n/2是奇数：a=n/2-2,b=n/2+2。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define ll long long
using namespace std;
ll T,n,ans;
int main()
{
    scanf("%lld",&T);
    while(T--)
    {
        ans=0;
        scanf("%lld",&n);
        if(n==2){printf("1\n");continue;}
        if(n<=1){printf("0\n");continue;}
        ll tmp1=0,tmp2=0;
        tmp1=n/2,tmp2=n-tmp1;
        if(tmp1==tmp2)
        {
            tmp1--,tmp2++;
            if(!(tmp1%2)) tmp1--,tmp2++;
        }
        ans=tmp1*tmp2;
        printf("%lld\n",ans);
    }
    return 0;
}

 

---

 

T2 题意简述：jzoj4424

 

Description

Input

Output

Data Constraint

 

   解题思路：分治FFT/NTT。

             由于博主太蒟蒻不会FFT或是NTT，因此没有代码。

             想看题解的戳这里。

 

---

 

T3 题意简述：jzoj4406

 

Description

有 2n 个人玩拔河，拔河的绳子由左右两段组成，每段绳子上有 n 个位置，第 i 个人可以在左边绳子的 l_i 位置处，也可以在右边绳子的 r_i 位置处。每个位置上有且仅有一个人。每个人有一个实力值 s_i ，问对于每一种合法方案两边实力值和之差的绝对值最小是多少，如果无解输出 -1 。

Input

第1行一个整数 n。
第2 ~ 2n+1行，每行三个整数l_i, r_i, s_i

Output

一个整数表示所求的答案

Data Constraint

30%：1 <= n <= 10
70%：1 <= n <= 10³
100%：1 <= n <= 3 * 10⁴, 1 <= s_i <= 15

 

   解题思路：二分图+背包。

             考虑在li，ri之间连一条权值为si的边，并记录各点度数。

             发现若有点度数为0则无解，若有点度数为1则该点结果唯一。

             因此可以把所有度数小于2的点进行处理，分别加到左右ans上。

             接下来图上只会剩下若干个偶环，考虑用背包解决剩下的问题。

             dfs求出在一个偶环中奇数边权值-偶数边权值的差，将其作为一个物品，做01背包即可。

             发现这样子时空都会炸，考虑单调队列滚动数组优化多重背包。

             感谢ZLX大佬教会博主上一行所述的操作。ZLX大佬OrzOrzOrz

             ZLX大佬还提供了背包的思路图：

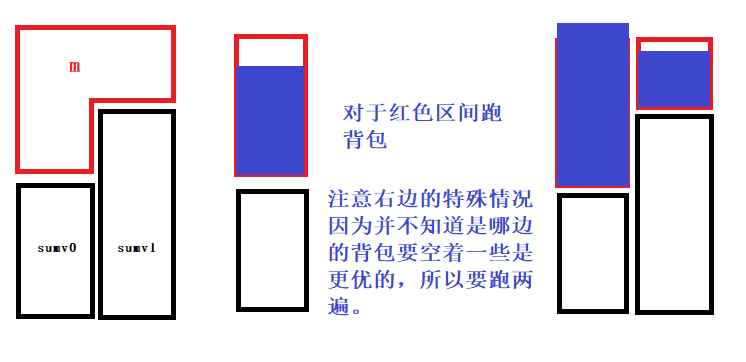
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<queue>
#include<map>
using namespace std;
int n,cnt=-1,ansl,ansr,d[60001],head[60001],vis[120001];
int m,sum,tot,wei[60001],num[60001],f[1200001],mi[60001],q[60001];
struct uio{
    int nxt,to,val;
}edge[120001];
queue<int> que;
map<int,int> mp;
void add(int x,int y,int z)
{
    edge[++cnt].nxt=head[x];
    edge[cnt].to=y;
    edge[cnt].val=z;
    head[x]=cnt;
}
void dfs(int x,int num)
{
    for(int i=head[x];i!=-1;i=edge[i].nxt)
    {
        int y=edge[i].to;
        if(vis[i]) continue;
        if(!num) sum+=edge[i].val;
        else sum-=edge[i].val;
        vis[i]=vis[i^1]=1;
        d[x]--,d[y]--;
        dfs(y,num^1);
    }
}
int dp(int m)
{
    memset(f,0,sizeof(f));
    int h,t;
    for(int i=1;i<=tot;i++)
    {
        if(!wei[i]) continue;
        int mn=min(num[i],m/wei[i]);
        for(int d=0;d<wei[i];d++)
        {
            h=t=1;
            for(int j=0;j<=(m-d)/wei[i];j++)
            {
                int tmp=f[j*wei[i]+d]-wei[i]*j;
                while(h<t&&q[t-1]<=tmp) t--;
                q[t]=tmp,mi[t]=j,t++;
                while(h<t&&j-mi[h]>mn) h++;
                f[j*wei[i]+d]=max(f[j*wei[i]+d],q[h]+wei[i]*j);
            }
        }
    }
    return f[m];
}
void solve()
{
    int l=dp((m+ansr-ansl)/2),r=dp((m+ansl-ansr)/2);
    int ans1=abs(ansl+l-(ansr+m-l));
    int ans2=abs(ansr+r-(ansl+m-r));
    printf("%d\n",min(ans1,ans2));
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d",&n);
    for(int i=1;i<=2*n;i++)
    {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        add(u,v+n,w),add(v+n,u,w);
        d[u]++,d[v+n]++;
    }
    for(int i=1;i<=2*n;i++)
    {
        if(!d[i]){printf("-1\n");return 0;}
        if(d[i]==1) que.push(i);
    }
    while(!que.empty())
    {
        int now=que.front();que.pop();
        for(int i=head[now];i!=-1;i=edge[i].nxt)
        {
            if(vis[i]) continue;
            int y=edge[i].to;
            if(now<=n) ansl+=edge[i].val;
            else ansr+=edge[i].val;
            vis[i]=vis[i^1]=1,d[now]--,d[y]--;
            if(d[y]==1) que.push(y);
        }
    }
    for(int i=1;i<=2*n;i++)
        if(d[i]==2)
        {
            sum=0,dfs(i,0);
            sum=abs(sum);m+=sum;
            if(!mp[sum]) mp[sum]=++tot,wei[tot]=sum;
            num[mp[sum]]++;
        }
    solve();
    return 0;
}