平衡树 x 01-trie √

本文将介绍一个使用01-trie实现平衡树的黑科技。

思路

排序树

性质：先序遍历01-trie时，依次经过的叶子节点所对应的数字依次递增。

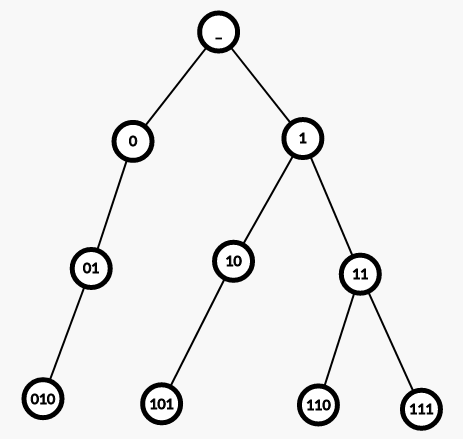
如图，向左的边表示0，向右的边表示1。

这是为什么呢？其实这就是二进制数比较大小的问题：比方说，0101和0011谁大？显然是前者。那么为什么0101比0011大呢？你可能会说，因为0101有三位，0011只有两位。

那么1101和1011谁大呢？还是前者。实际上你比较两个数字大小的时候，都是从高位向低位依次比较的。

注意：先比较高位。换到01-trie上，就是先比较高度小的。

那不就是先序遍历嘛！

也就是说，01-trie可以实现排序功能。

其他操作

插入、删除都是小case。我们以P3369 【模板】普通平衡树作为平衡树的“基本操作”。

查询排名

每个数都对应01-trie上从根到叶子节点的一条链。那么，每个数都可以把一颗01-trie分成两部分：

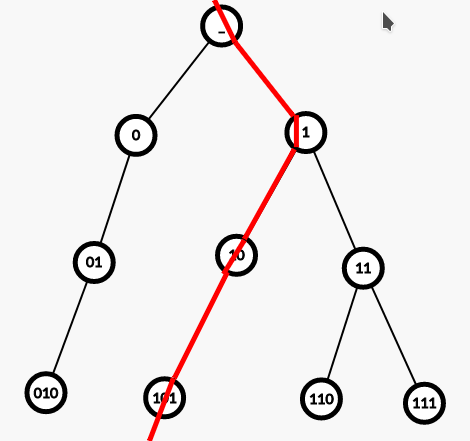
根据刚才证明的性质，那么这个数左边的数都比它小，右边的都比它大，那么只需要统计它左边有多少数即可。

查询第k大

查询排名的逆操作。思路同其他的平衡树，不再赘述。

前驱（后继）

从这个数对应的叶子节点开始，不断往上爬，如果当前节点有左（右）子树且不是刚才爬上来的那颗，那么进入这颗子树并在这颗子树内找到一个最大（小）的数。

其实还可以查询第k大(查询排名(x)-1)

代码

#include <cmath>
#include <cstdio>
#include <cstring>
template <class T>
inline void read(T &num)
{
    bool flag = 0;
    num = 0;
    char c = getchar();
    while ((c < '0' || c > '9') && c != '-')
        c = getchar();
    if (c == '-')
    {
        flag = 1;
        c = getchar();
    }
    num = c - '0';
    c = getchar();
    while (c >= '0' && c <= '9')
        num = (num << 3) + (num << 1) + c - '0', c = getchar();
    if (flag)
        num *= -1;
}
template <class T>
inline void output(T num)
{
    if (num < 0)
    {
        putchar('-');
        num = -num;
    }
    if (num >= 10)
        output(num / 10);
    putchar(num % 10 + '0');
}
template <class T>
inline void outln(T num)
{
    output(num);
    putchar('\n');
}
template <class T>
inline void outps(T num)
{
    output(num);
    putchar(' ');
}
inline void ln()
{
    putchar('\n');
}
template <class T>
inline T max(T a, T b)
{
    return a < b ? b : a;
}
struct node
{
    node *ch[2];
    int siz;
    node()
    {
        ch[0] = ch[1] = NULL;
        siz = 0;
    }
} * root;
const int W = 25;
void ins(int x)
{
    node *p = root;
    for (int i = W - 1; i >= 0; i--)
    {
        bool now = (x >> i) & 1;
        if (p->ch[now] == NULL)
            p->ch[now] = new node;
        p->siz++;
        p = p->ch[now];
    }
    p->siz++;
}
void del(int x)
{
    node *p = root, *ch;
    for (int i = W - 1; i >= 0; i--)
    {
        bool now = (x >> i) & 1;
        ch = p->ch[now];
        p->siz--;
        if (ch->siz == 1)
            p->ch[now] = NULL;
        if (p -> siz == 0)
            delete p;
        p = ch;
    }
    p->siz--;
}
int rk(int x)
{
    int rtn = 0;
    node *p = root;
    for (int i = W - 1; i >= 0; i--)
    {
        bool now = (x >> i) & 1;
        if (now == 1 && p->ch[0] != NULL)
            rtn += p->ch[0]->siz;
        if (p->ch[now])
            p = p->ch[now];
        else
            break;
    }
    return rtn + 1;
}
int get(int x)
{
    int rtn = 0;
    node *p = root;
    for (int i = W - 1; i >= 0; i--)
    {
        if (p->ch[0] == NULL)
        {
            p = p->ch[1];
            rtn = rtn << 1 | 1;
        }
        else if (p->ch[1] == NULL || p->ch[0]->siz >= x)
        {
            p = p->ch[0];
            rtn = rtn << 1;
        }
        else
        {
            x -= p->ch[0]->siz;
            p = p->ch[1];
            rtn = rtn << 1 | 1;
        }
    }
    return rtn;
}
int pre(int x)
{
    int rtn, fx = 0;
    node *p = root, *lst;
    for (int i = W - 1; i >= 0; i--)
    {
        bool now = (x >> i) & 1;
        if (now == 1 && p->ch[0] != NULL)
        {
            lst = p->ch[0];
            rtn = fx << 1;
        }
        if (p->ch[now])
            p = p->ch[now];
        else
            break;
        fx = fx << 1 | now;
    }
    while (lst)
    {
        if (lst->ch[1])
            lst = lst->ch[1], rtn = rtn << 1 | 1;
        else
            lst = lst->ch[0], rtn = rtn << 1;
    }
    return rtn >> 1;
}
int nxt(int x)
{
    int rtn, fx = 0;
    node *p = root, *lst;
    for (int i = W - 1; i >= 0; i--)
    {
        bool now = (x >> i) & 1;
        if (now == 0 && p->ch[1] != NULL)
        {
            lst = p->ch[1];
            rtn = fx << 1 | 1;
        }
        if (p->ch[now])
            p = p->ch[now];
        else
            break;
        fx = fx << 1 | now;
    }
    while (lst)
    {
        if (lst->ch[0])
            lst = lst->ch[0], rtn = rtn << 1;
        else
            lst = lst->ch[1], rtn = rtn << 1 | 1;
    }
    return rtn >> 1;
}
void dfs(node *node, int num)
{
    if (node == NULL)
        return;
    dfs(node->ch[0], num << 1);
    dfs(node->ch[1], num << 1 | 1);
    if (node->ch[0] == NULL && node->ch[1] == NULL)
        outln(num);
}
const int delta = 10000001;
int n;
int main()
{
    root = new node;
    read(n);
    for (int i = 1; i <= n; i++)
    {
        int opt, x;
        read(opt);
        read(x);
        if (opt == 1)
            ins(x + delta);
        if (opt == 2)
            del(x + delta);
        if (opt == 3)
            outln(rk(x + delta));
        if (opt == 4)
            outln(get(x) - delta);
        if (opt == 5)
            outln(pre(x + delta) - delta);
        if (opt == 6)
            outln(nxt(x + delta) - delta);
    }
}