单源最短路算法
知识点
- dijkstra算法
- 堆优化的dijkstra算法
- SPFA算法
求单源最短路的暴力解法
1.枚举
Bellman-Ford算法好像长得比较像枚举
2.DFS应该不可做
3.BFS解法
伪代码如下：
void bfs(int s) {
新建一个队列;
visited全都赋值为false;
dis全都赋值为无穷大;
dis[s] = 0;
s入队;
visited[s] = true;
while (队列非空) {
x = 队首元素;
队首元素出队;
for (从x出发的所有边e) {
if (dis[e的终点] > dis[x] + e的长度)
dis[e的终点] = dis[x] + e的长度;
if (visited[e的终点] == false) {
把e的终点入队;
visited[e的终点] = true;
}
}
}
}
然而这个做法是错误的。
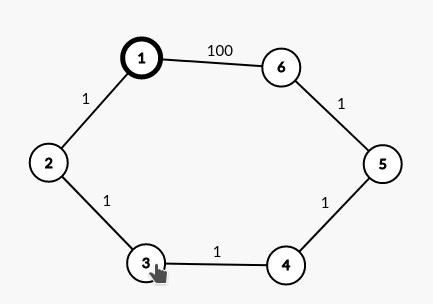
如上图。模拟过程如下：
调用
bfs(1)
dis[1]赋值为0，1入队1出队
dis[2]赋值为1，2入队
dis[6]赋值为100，6入队2出队
dis[3]赋值为2，3入队6出队
dis[5]赋值为101，5入队3出队
dis[4]赋值为3，4入队5出队
不更新dis[4]，4不入队（因为visited[4]为true）4出队
dis[5]赋值为4，5不入队（因为visited[5]为true）然后你就会惊喜的发现
dis[6]应该是5而不是这段代码所算出来的100
那么怎么解决这个问题呢？
A 防止“锁死”
不妨设想一下，如果在最后一步访问4的时候，我们把5入队了：
...（前略）
4出队
dis[5]赋值为4，5入队5出队
dis[6]赋值为5，6不入队（因为visited[6]为true）
这样算出来的答案是对的。
所以visited是内鬼
能不能去掉visited数组或者改成别的东西呢？
SPFA算法
先上代码
void bfs(int s) {
新建一个队列;
visited全都赋值为false;
dis全都赋值为无穷大;
dis[s] = 0;
s入队;
visited[s] = true;
while (队列非空) {
x = 队首元素;
队首元素出队;
visited[x] = false; // 加上这一行
for (从x出发的所有边e) {
if (dis[e的终点] > dis[x] + e的长度)
dis[e的终点] = dis[x] + e的长度;
if (visited[e的终点] == false) {
把e的终点入队;
visited[e的终点] = true;
}
}
}
}
这啥？
可以发现，visited[x]表示x是否在队列里。
然而这段代码显然不对，它会无限循环。
再改一下。
void bfs(int s) {
新建一个队列;
visited全都赋值为false;
dis全都赋值为无穷大;
dis[s] = 0;
s入队;
visited[s] = true;
while (队列非空) {
x = 队首元素;
队首元素出队;
visited[x] = false;
for (从x出发的所有边e) {
if (dis[e的终点] > dis[x] + e的长度) {
dis[e的终点] = dis[x] + e的长度;
if (visited[e的终点] == false) { // 把这个if移到上一个if里边来了
把e的终点入队;
visited[e的终点] = true;
}
}
}
}
}
为什么这样不会死循环呢？
原因在于，如果每个点的dis都已经正确地求出来了，那么第13行的if根本不会触发。（除非有负权回路）
正确性（选讲）
首先了解一下Bellman-Ford算法。
非常简洁的一个算法，每次循环依次枚举图中每条边，如果发现dis[这条边的终点]>dis[这条边的起点]+这条边的长度就把dis[这条边的终点]赋值为dis[这条边的起点]+这条边的长度。重复循环n-1次。
for (int i = 1; i <= n - 1; ++i)
for (图中所有边e)
if (dis[e的终点] > dis[e的起点] + e的长度)
dis[e的终点] = dis[e的起点] + e的长度;
为什么它是正确的？
因为图中只有n个点，从起点出发到达任何一个点，最多也就走n-1步（或者说，经过n-1条边）（除非有负权回路）
最坏的情况：图是一条链，且每次都是从终点方向往起点方向枚举
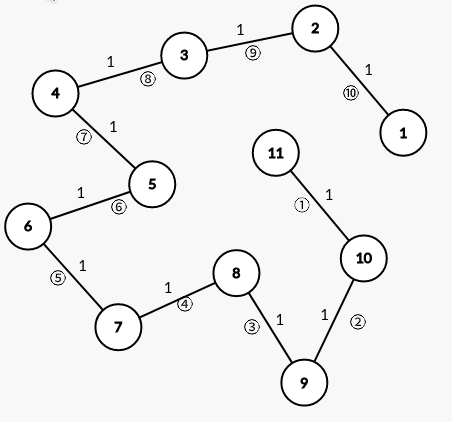
只要图中还有未求出最短距离的点，每次循环它都会更新至少一个点的dis。由于dis[s]已知，所以我们最多再循环n-1次即可求得正确答案。
然而这个算法太慢了。特别是第一次循环的时候，能求出dis的其实只有与起点直接相连的那些点，而我们却仍然遍历了所有的边。
为此，我们有“队列优化的Bellman-Ford算法”，也就是SPFA。
SPFA相对于Bellman-Ford算法所做的优化：每次循环不再是枚举所有的边，而是枚举队列的点相连的边。那么什么样的点会放进队列里呢？上一次循环的时候dis值发生了变化的点。
于是我们成功的证明了SPFA算法的正确性（？
B 改变bfs顺序
下面假设图中所有边的长度都是正数。
引理1：一定存在一条边，连接 起点 与 距离起点最近的点；或者说，距离起点最近的点一定与起点之间直接有边相连。
定理1：起点 到 距离起点最近的点 的最短距离等于连接这两个点的边的长度。
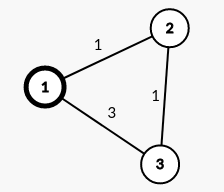
如上图，1是起点，那么1到2的最短距离就一定是1；反之，3不是距离1最近的点，那么1到3的最短距离就不一定是3（本例中是2）
定理1的推广：如果把 起点 和 距离起点最近的点 合并为一个点，那么上述定理仍可使用。
定理1的推广的推广：该推广可多次反复使用。
原图：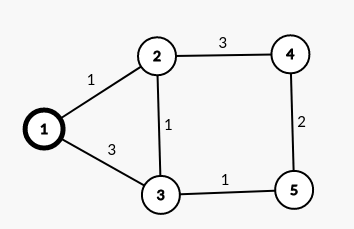
此时距离1最近的点是2，最短距离是1
第一次合并：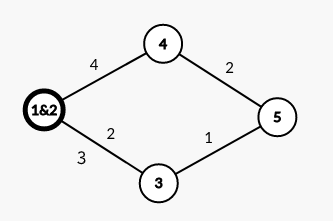
此时距离1&2最近的点是3，最短距离是2
第二次合并：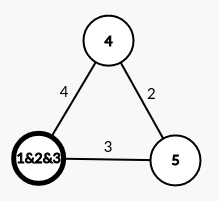
此时距离1&2&3最近的点是5，最短距离为3
第三次合并：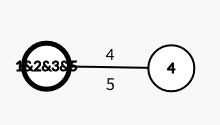
此时距离1&2&3&5最近的点是4，最短距离是4
最终结果：dis[2] = 1 dis[3] = 2 dis[4] = 4 dis[5] = 3
问题来了：这个性质咋用？喵喵喵？
再看一下刚才那个图：
如果我们按照1 - 2 - 3 - 4 - 5 - 6的顺序进行搜索，好像就能得到正确答案吧？
Dijkstra算法（堆优化版）
既然是“队列”这个数据结构导致答案错误，那就干脆不！用！了！
现在假想一种数据结构，叫
水池子
“倒”进去的元素会自动按照“密度”从大到小排列。
你可以从顶上往外“舀”。
人话：自动将内部元素排序，支持取出最小/大值
我们现在考虑用这样的一个数据结构来代替队列。
根据定理1，距离“起点”最近的点算出来的dis值一定是正确的。
也就是说，如果“水池子”里有多个待搜索的节点，我们可以先搜索距离起点近的点。
void bfs(int s) {
新建一个水池子;
visited全都赋值为false;
dis全都赋值为无穷大;
dis[s] = 0;
s倒进水池子里;
visited[s] = true;
while (水池子非空) {
x = 水池子里距离s最近的点;
把x从水池子里舀出来;
for (从x出发的所有边e) {
if (dis[e的终点] > dis[x] + e的长度)
dis[e的终点] = dis[x] + e的长度;
if (visited[e的终点] == false) {
把e的终点倒进水池子里;
visited[e的终点] = true;
}
}
}
}
模拟一下过程：
调用
bfs(1)
dis[1]赋值为0，1入水池子1出水池子
dis[2]赋值为1，2入水池子
dis[6]赋值为100，6入水池子2出水池子
dis[3]赋值为2，3入水池子3出水池子
dis[4]赋值为3，4入水池子4出水池子
dis[5]赋值为4，5入水池子5出水池子
dis[6]赋值为5，6不入水池子（因为visited[6]为true）6出水池子
答案对了！
问题：如何维护这样的一个水池子
堆
没学的话可以先跳过
void bfs(int s) {
新建一个堆;
visited全都赋值为false;
dis全都赋值为无穷大;
dis[s] = 0;
s入堆;
visited[s] = true;
while (堆非空) {
x = 堆顶;
堆顶元素出堆;
if (visited[x] == true) continue;
visited[x] = true;
for (从x出发的所有边e) {
if (dis[e的终点] > dis[x] + e的长度)
dis[e的终点] = dis[x] + e的长度;
e的终点入堆,权值为 dis[e的终点];
}
}
}
不带堆优化的dijkstra算法
堆优化的版本都懂了 不带堆优化的不就直接会了啊
堆优化的dijkstra算法使用堆来查找“距离起点最近的点”；不带堆优化的dijkstra算法是暴力找这个“距离起点最近的点”。其他都一样。
for (int i = 1; i <= n; ++i) {
int x, d = 无穷大;
for (int p = 1; p <= n; ++p) {
if (visited[p] == false && dis[p] < d) {
x = p;
d = dis[p];
}
}
visited[p] = true;
for (从x出发的所有边e) {
if (dis[e的终点] > dis[x] + e的长度)
dis[e的终点] = dis[x] + e的长度;
}
}
总结
只要没有负权边，就写堆优化的dijkstra；有负权边就写SPFA。
题
模板：
U69305 【常数PK系列】 #2 单源最短路（备注：我出的；它 非 常 有 意 思）
洛谷官方题单：
代码
P3371
#include<bits/stdc++.h>
#define inf 2147483647
using namespace std;
int n,m,s;
struct edge{
int to,dis;
edge(int a,int b):to(a),dis(b){}
};
vector<edge>edges;
vector<int>G[10003];
void add_edge(int u,int v,int w){
edges.push_back(edge(v,w));
G[u].push_back(edges.size()-1);
}
struct node{
int p,dis;
node(int a,int b):p(a),dis(b){}
};
bool operator< (node a,node b){
return a.dis>b.dis;
}
priority_queue<node>q;
int d[10003];
bool u[10003];
int main(){
cin>>n>>m>>s;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
add_edge(u,v,w);
}
fill(d+1,d+n+1,inf);
d[s]=0;
q.push(node(s,0));
while(!q.empty()){
node x=q.top();
q.pop();
//cout<<x.p<<' '<<x.dis<<endl;
if(u[x.p])continue;
u[x.p]=1;
for(int i=0;i<G[x.p].size();i++){
edge e=edges[G[x.p][i]];
//cout<<'\t'<<e.to<<' '<<d[e.to]<<"->";
d[e.to]=min(d[e.to],d[x.p]+e.dis);
//cout<<d[e.to]<<endl;
q.push(node(e.to,d[e.to]));
}
}
for(int i=1;i<=n;i++){
cout<<d[i]<<' ';
}
}
U69305
#include<bits/stdc++.h>
using namespace std;
int n,m,s,t;
int fir[250001],to[1000001],nxt[1000001],dis[1000001],ecnt;
void add(int u,int v,int w){
to[++ecnt]=v;
dis[ecnt]=w;
nxt[ecnt]=fir[u];
fir[u]=ecnt;
}
struct node
{
int id;
unsigned long long dis;
node(int id,unsigned long long dis):id(id),dis(dis){}
};
bool operator<(node a,node b){
return a.dis>b.dis;
}
priority_queue<node>q;
bool vis[250001];
unsigned long long d[250001];
int main(){
cin>>n>>m>>s>>t;
for(int i=1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
add(u,v,w);
add(v,u,w);
}
fill(d+1,d+n+1,ULONG_LONG_MAX-INT_MAX);
q.push(node(s,0));
d[s]=0;
while(!q.empty()){
node h=q.top();
q.pop();
if(vis[h.id])continue;
vis[h.id]=1;
for(int e=fir[h.id];e;e=nxt[e]){
if(!vis[to[e]]&&d[to[e]]>dis[e]+h.dis){
d[to[e]]=dis[e]+h.dis;
q.push(node(to[e],d[to[e]]));
}
}
}
cout<<d[t]<<endl;
}
