Tarjan学习笔记
强连通分量,缩点算法:Tarjan
代码及模板
前言:前期先要把Tarjan的思想领悟到,但是有很多算法的核心思路就是Tarjan,所以在代码中一般都把这些算法的函数名写作Tarjan,但这些Tarjan是有细小区别的,中后期一定要注意区分这些算法的区别。
强连通图:有向图,任意两点有路径
强连通分量:有向图,强连通子图数量
前置知识:dfs树(dfs序构成的树)(没学过也没关系,这玩意最多只是帮助理解)
成分:
- 树边:dfs树上的边
(以下三种边是dfs树上没有但原图上有的边) - 前向边:dfs树的祖先到儿子的边。
- 返祖边(后向边):儿子到祖先的边
- 横向边:旁系亲戚的边(没有直接的祖父关系,可能是兄弟节点之类的)
Tarjan算法是在dfs中实现的。
如果要感性地理解,Tarjan会去不停地找一个类似于环一样的东西,然后把环上的节点的low全部更新为环上最小的dfn。
对于Tarjan算法,我们需要
- 一个dfn数组,也就是dfs序,(只要是之前搜索过的点,都有dfn值(废话),所以还可以记录该点目前有没有访问过)。
- 一个low数组,按我的理解来说就是记录在该scc中的店,dfn(dfs序)最小的点的dfn。
- (部分Tarjan算法)需要一个栈,在栈中的元素是还没有确定该点的scc是哪一个的点,就是还可能会继续更新的点。
- (部分Tarjan算法)一个bool数组,记录某个点x,是否在上文所说的栈中。
对于有向图强连通分量(scc)的Tarjan求法,我们需要(上面四个全都要)
- 一个dfn数组,也就是dfs序,(只要是之前搜索过的点,都有dfn值(废话),所以还可以记录该点目前有没有访问过)。
- 一个low数组,按我的理解来说就是记录在该scc中的点,dfn(dfs序)最小的点的dfn。
- 需要一个栈,在栈中的元素是还没有确定该点的scc是哪一个的点,就是还可能会继续更新的点。
- 一个bool数组,记录某个点x,是否在上文所说的栈中。
现在搜索到了节点u,原图上有一条u—>v的边。
情况1 :节点v还没被遍历,具体表现为"dfn[v]==0",那么直接搜索节点v,并用节点v的min值更新节点u。
具体来讲,每次递归v的时候,都要把 low[u] 更新为 min(low[u], low[v])。因为v节点有可能找到了返祖边,那么父节点的low也是儿子的low
情况2 :节点v已经在搜索过了,并且还在栈中,那么u,v就在同一个scc(强联通分量)中,并且一定有dfn[u] < dfn[v](因为v先被搜索到)。
这时候u->v这条边就是一条返祖边,所以要把low[u]更新成 min(low[u], dfn[v])。
情况3 :节点v被搜索过,但是不在栈里,说明这是一条横向边,横向边的两端点点不在同一个scc中,直接不管。
(强烈建议画图理解,手模后可以加深理解)
循环结束后,如果low[u] = dfn[u],说明u是环的根,栈后面的元素都属于该强联通图,染色,出栈。
具体的代码实现有点有趣。
#include <stack>
int dfn[MAXN], tot = 0;
bool instack[MAXN];
int low[MAXN];
int co[MAXN], col = 0;
std::stack<int> stk;
void Tarjan(int u)
{
dfn[u] = ++tot;
low[u] = dfn[u]; // 一开始low[u]是自己,有后向边再更新
stk.push(u);
instack[u] = true;
for(int e = first[u]; e; e = nxt[e])
{
int v = go[e];
if(!dfn[v])
{
Tarjan(v);
low[u] = min(low[u], low[v]); // 子节点更新了,我也要更新
// 若子节点没更新,则min能够保证low[u] == dfn[u]
}
else if(instack[v]) // v访问过且在栈中,意味着u→v是后向边
{
low[u] = min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]) // 是SCC中的第一个被访问的节点
{
co[u] = ++col;
while(stk.top() != u) co[stk.top()] = col, instack[stk.top()] = false, stk.pop();
// 染色,弹栈
instack[u] = false;
stk.pop(); // 最后把u弹出去
}
}
缩点
即把同一强连通分量的点变成一个点,新点权为scc里所有点权之和(根据具体需求,有的时候新点权是其它东西)。
割点
'前言:后被遍历到的点dfn更大。(这不纯废话吗?)'
简单的定义:删了该点图不连通的点叫割点
换句话说:若x是割点,则存在 y∈T(x) 满足y不经过 x 能到达的所有点均属于 T(x)。(注:T(x)表示x的dfs子树)
如果有儿子节点的low大于等于
割边(桥)
当枚举到边u->v时,若low_v > low_u时,该边为桥。
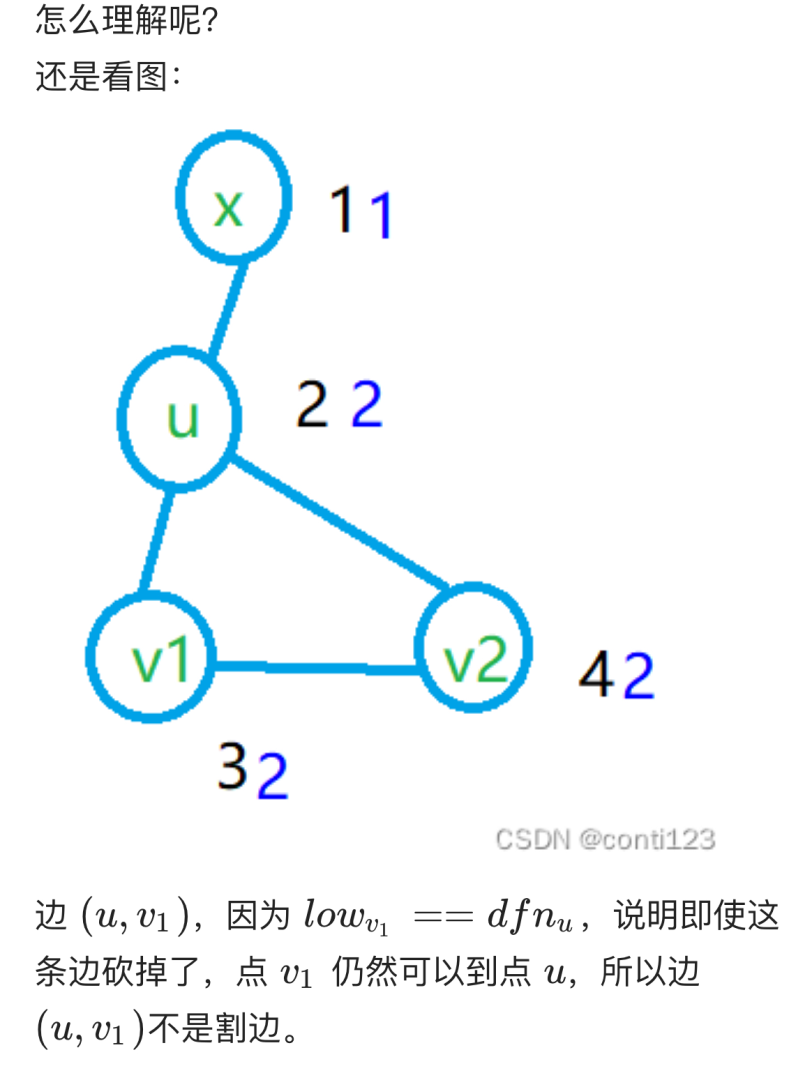
所以说,割点是大于等于,而割边只是大于。
边,点双连通分量(不摆了,直接抄的oi-wiki)
定义:
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 u 和 v 边双连通。
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪个点(只能删去一个,且不能删 u 和 v 自己)都不能使它们不连通,我们就说 u 和 v 点双连通。
边双连通具有传递性, 而点双连通不具有传递性
一个边/点双连通分量 == 边/点双连通子图
边双连通分量求法:
在 DFS 生成树上的一个强连通分量,在原无向图中是边双连通分量。可以发现,求边双连通分量的过程实际上就是求强连通分量的过程。
最后记得判重边****
桥(割边)的求法
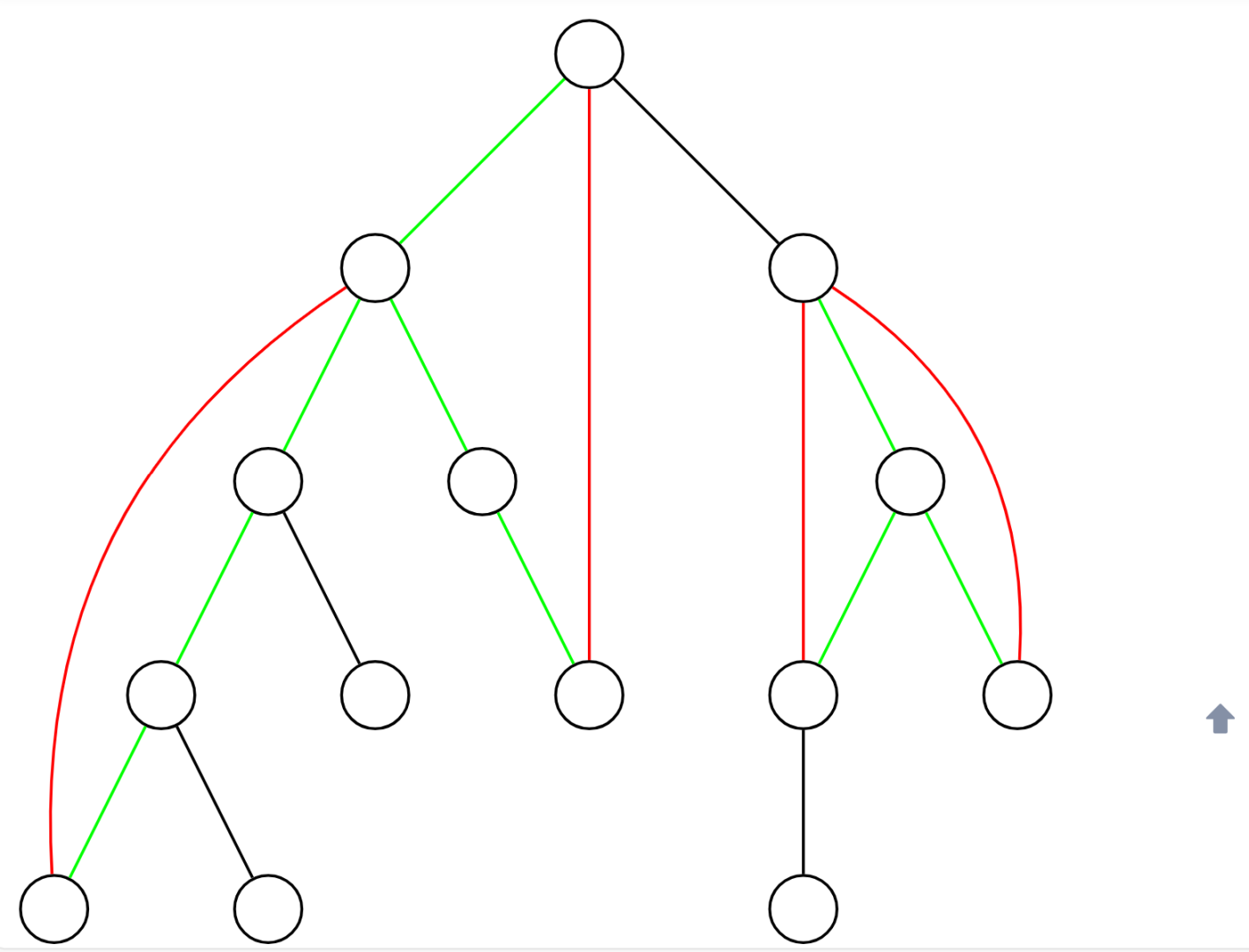
如上图所示,黑色与绿色边为树边,红色边为非树边。每一条非树边的两个端点都唯一对应了树上的一条由树边构成的简单路径,我们说这条非树边 覆盖 了这条简单路径上所有的边。
在图中,绿色的树边 至少 被一条非树边覆盖,黑色的树边不被 任何 非树边覆盖。
显然,非树边 和 绿色的树边 一定不是桥,黑色的树边 一定是桥。
首先考虑一个暴力的做法,对于每一条非树边,都逐个地将它覆盖的每一条树边置成绿色,时间复杂度为 O(nm)。
考虑用差分优化。对于每一条非树边,在其树上深度较小的端点处打上 -1 标记,在其树上深度较大的端点处打上 +1 标记,然后 O(n) 求出每个点的子树内部的标记和。
对于一个点 u,其子树内部的标记之和等于覆盖了 u 和 fa_u 之间的树边的非树边数量。若这个值等于 0,则 u 和 fa_u 之间的树边是 桥。
void TJ(int u, int fa){
dfn[u] = ++cnt, low[u] = dfn[u]; sta.push(u);
for(auto v : edge[u]) if(v != fa)/*防止回环*/{
if(!dfn[v]) TJ(v, u);
low[u] = min(low[u], low[v]);
}//只要不是父亲节点来的边,都可以去更新low[u]
if(dfn[u] == low[u]){//染色
co[++col].push_back(u);
while(sta.top() != u) {
int x = sta.top();
scc[x] = col;
co[col].push_back(x), sta.pop();
}
scc[u] = col;
sta.pop();
}
}//我自创的优美边双写法
点双的求法 模板
可能有且只有割点可能同时存在两个点双图中。
每遇到一个割点(见割点的求解方法),就弹出一些点放到一个点双中。
void TJ(int u, int rt) {
dfn[u] = low[u] = ++ tot;
if(u == rt && !edge[u].size()) //孤立点的特判
scc[++ col].push_back(u);
stk[++ tp] = u;
for(auto v : edge[u]) {
if(!dfn[v]) {
TJ(v, rt);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) {//点u一定为割点
scc[++ col].push_back(u);
while(stk[tp] != v) {//割点点u不会被弹出
scc[col].push_back(stk[tp]);
-- tp;
}
scc[col].push_back(stk[tp]);
-- tp;
//注意到 if(low[v] >= dfn[u])是在TJ(v)后的,所以实际执行时间比较晚
//故弹栈中元素最多只能弹到v,剩下的元素要让之前的某个u(dfn更小的节点)来弹出
}
}
else low[u] = min(low[u], dfn[v]);//注意这里不用去判断v是否在栈中
}
}
圆方树:先用Tarjian找点双,对于每一个点双,构建一个方点(一个虚空点),然后把每个点双上原来的点与这个新构建的方点连边,边上记录该点的信息(如边权,点权等)。
用处:可以把图变成树的同时任然保留原来点的信息。
(个人感觉圆方树就是一种特别的缩点方式)
狭义的圆方树是用来解决仙人掌图的问题的,那什么是仙人掌图呢?即不存在边同时属于多个环的无向连通图是一棵仙人掌。
如果把一个环当成一个节点,那么仙人掌就是一颗普通的树。恰当地使用园方树可以将环处理成等价的一些边,可以把图上问题转化成树上问题。
最后补充一个Tarjan的应用:2-SAT问题






【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 推荐几款开源且免费的 .NET MAUI 组件库
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· Trae初体验