树状数组

树状数组

一、长什么样？

假设有一数组a，数组b为a的前缀和数组，即b[i] = a[i] + a[i-1] + ... + a[1]，树状数组c为a的（部分）前缀和数组，即c[i] = a[i] + a[i-1] + ... + a[i+1-lowbit(i)]，也即c[i]为lowbit(i)个数组a的元素的和。

lowbit(i): 把i以二进制展开，只留下最低位的1及其后的0，其余位清零后所得的数值。注意i & -i可以直接算出这个值。

上述方式所得的数组c中每个元素对应的数组a元素和的个数，由下图可以看得很清晰，注意第一个元素从下标1开始。

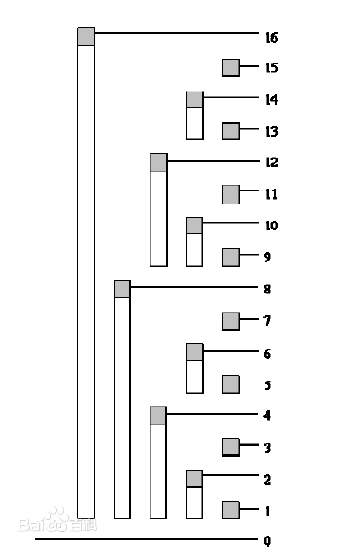
alt 树状数组

进一步，求b[i]可以用x个数组c中的元素相加，其中x = 数字i的二进制展开中bit1的个数，具体由哪几个元素相加看图容易得到，下标的计算可以参考具体的代码。动态更新a[i]时，需要更新b[j]，其中b[j] = a[j] + ... + a[i] + ... ，即含a[i]的数组b中的元素都需要被更新。

若用普通数组动态维护前缀和，复杂度为O(n)，若用树状数组，由二进制展开的特性易知复杂度则为O(logn)，看图也易得。

二、怎么维护？

1.单点修改 区间查询（查询区间和）

  • 初始化树状数组c为0（第一个元素下标为1, 下标为0的元素也要初始化为0）

  • 原数组a的第x个元素加v

    void add(int x, int v) { 
	while (x <= n) {
		c[x] += v; //c为a对应的树状数组
		x += lowbit(x); 
	}
}

  • 求原数组a中第一个至第x个元素的和

    int sum(int x) {
	int t = 0;
	while (x) {
		t += c[x];
		x -= lowbit(x);
	}
	return t;
}

  • 区间[x1, x2]和查询

    int query(int x1, int x2) {return sum(x2) - sum(x1 - 1);}
2.区间修改，单点查询（对区间内所有值加上某一值）

思路：差分，设差分数组p，则p[i] = a[i] - a[i-1]=>a[i] = p[i] + p[i-1] + ... + p[1]。维护差分数组p的树状数组即可。
add() sum()的实现同单点修改，区间查询。

  • 初始化树状数组c为0

  • 初始化赋值时要注意维护的是差分数组p对应的树状数组c。例如：在原数组a下标为x处初始化为v，对应于在数组p中给p[x]初始化为v-p[x-1]。（p的初值置为0）

    add(x, v - sum(x-1)); //按下标连续初始化时不用调用sum()

  • 原数组a中下标在[x1, x2]范围的值均加上某值v，对应于在数组p中给p[x1]加v，给p[x2+1]减v

    add(x1, v), add(x2 + 1, -v);

  • 查询原数组a中下标为x的值，对应于求p[x] + p[x-1] + ... + p[1]，即求p的某前缀和

    sum(x);
3.区间修改，区间查询

由区间修改，单点查询的基础上，优化一下区间查询的效率即可。首先推一下公式，随便截了个图，该图的描述方法和之前的有些不同。

di为差分数组的第i个元素，an为原数组第n个元素。公式表示原数组的前缀和，等价变换可得，原数组的前缀和可以转化为差分数组的前缀和以及di*i的前缀和。故得一思路：通过树状数组维护差分数组的前缀和，再通过公式计算出原数组的前缀和。

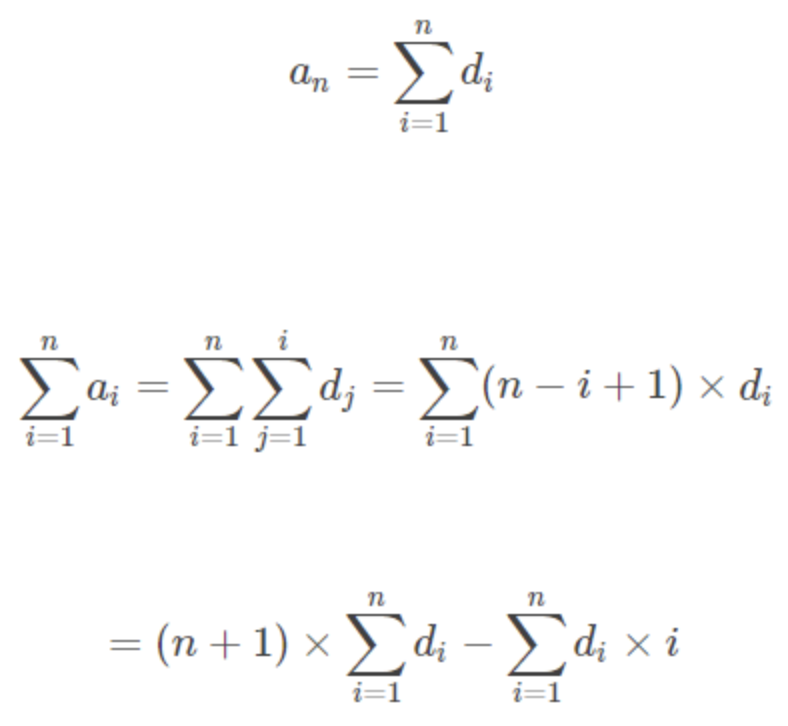
alt 公式

  • add() sum()稍作修改：

    void add(int x, int v, int *a) {
  while (x <= n) {
    a[x] += v;
    x += lowbit(x);
  }
}

int sum(int x, int *a) {
  int ret = 0;
  while (x) {
    ret += a[x];
    x -= lowbit(x);
  }
  return ret;
}

  • 初始化树状数组为0

  • 初始化赋值：维护差分数组的同时维护数组array，其中array[i] = di * i，具体初始化的方法与区间修改，单点查询的情况类似。设在原数组a下标为x处初始化为v。

    int t = v - sum(x-1); //按下标连续初始化时不用调用sum()
add(x, t, 差分数组的指针);
add(x, t * x, array的指针);

  • 原数组中下标在[x1, x2]范围的值均加上某值v

    add(x1, v, 差分数组的指针), add(x2 + 1, -v, array的指针); 
add(x1, v * x1, 差分数组的指针), add(x2 + 1, -v * (x2 + 1), array的指针);

  • 查询原数组[x1, x2]区间和为

    ( (x2 + 1) * sum(x2, 差分数组的指针) - sum(x2, array的指针) )
		- ( x1 * sum(x1 - 1, 差分数组的指针) - sum(x1 - 1, array的指针) );

三、模版题各一道。。

1单点修改，区间查询 洛谷P3374

#include <cstdio>
const int N = 500000 + 20;

int n, m, c[N];
inline int read() {
	int x = 0, f = 1; char ch = getchar();
	while ('0' > ch || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
	while ('0' <= ch && ch <= '9') {x = 10 * x + ch - '0'; ch = getchar();}
	return x * f;
}

inline int lowbit(int x) {return x & -x;}

void add(int x, int v) {
	while (x <= n) {
		c[x] += v;
		x += lowbit(x);
	}
}

int sum(int x) {
	int t = 0;
	while (x) {
		t += c[x];
		x -= lowbit(x);
	}
	return t;
}

int main() {
	n = read(), m = read();
	for (int i = 1; i <= n; i++) add(i, read());
	while (m--) {
		int cmd = read(), k1 = read(), k2 = read();
		if (cmd == 1) add(k1, k2);
		else printf("%d\n", sum(k2) - sum(k1 - 1));
	}
	return 0;
}

2区间修改，单点查询 洛谷P3368

#include <cstdio>
const int N = 500000 + 20;
int n, m, c[N];

inline int read() {
	int x = 0, f = 1; char ch = getchar();
	while ('0' > ch || ch > '9') {if (ch == '-') f = -1; ch = getchar();}
	while ('0' <= ch && ch <= '9') {x = 10 * x + ch - '0'; ch = getchar();}
	return x * f;
}

inline int lowbit(int x) {return x & -x;}

void add(int x, int v) {
	while (x <= n) {
		c[x] += v;
		x += lowbit(x);
	}
}

int sum(int x) {
	int t = 0;
	while (x) {
		t += c[x];
		x -= lowbit(x);
	}
	return t;
}

int main() {
	n = read(), m = read();
	int last = 0, t;
	for (int i = 1; i <= n; i++) {
		t = read();
		add(i, t - last);
		last = t;
	}
	while (m--) {
		int cmd = read();
		if (cmd == 1) {
			int x = read(), y = read(), k = read();
			add(x, k), add(y + 1, -k);
		} else {
			int x = read();
			printf("%d\n", sum(x));
		}
	}
	return 0;
}

3区间修改，区间查询 poj3468

#include <cstdio>
#include <cstring>
typedef long long ll;
const int N = 100000 + 10;
ll n, q;
ll num1[N], num2[N];

inline ll lowbit(ll x) {return x & (-x);}
void add(ll x, ll v, ll *a) {
	while (x <= n) {
		a[x] += v;
		x += lowbit(x);
	}
}

ll sum(ll x, ll *a) {
	ll ret = 0;
	while (x) {
		ret += a[x];
		x -= lowbit(x);
	}
	return ret;
}

inline ll query(ll a, ll b) {
	return (b + 1) * sum(b, num1) - sum(b, num2) 
		- (a * sum(a - 1, num1) - sum(a - 1, num2));
}

int main() {
	scanf("%lld%lld", &n, &q);
	ll last = 0, t;
	for (int i = 1; i <= n; i++) {
		scanf("%lld", &t);
		add(i, t - last, num1);
		add(i, (t - last) * i, num2); //一开始写成num1。。
		last = t;
	}
	char line[30];
	ll a, b, c;
	getchar(); //别忘了。。
	while (q--) {
		gets(line);
		if (line[0] == 'Q') {
			sscanf(line + 1, "%lld%lld", &a, &b);
			printf("%lld\n", query(a, b));
		} else {
			sscanf(line + 1, "%lld%lld%lld", &a, &b, &c);
			add(a, c, num1);
			add(b + 1, -c, num1);
			add(a, c * a, num2);
			add(b + 1, -c * (b + 1), num2);
		}
	}
	return 0;
}

`

posted @ 2020-02-14 21:27  watchphone  阅读(96)  评论(0)  编辑  收藏  举报