OO第一单元博客作业
类图
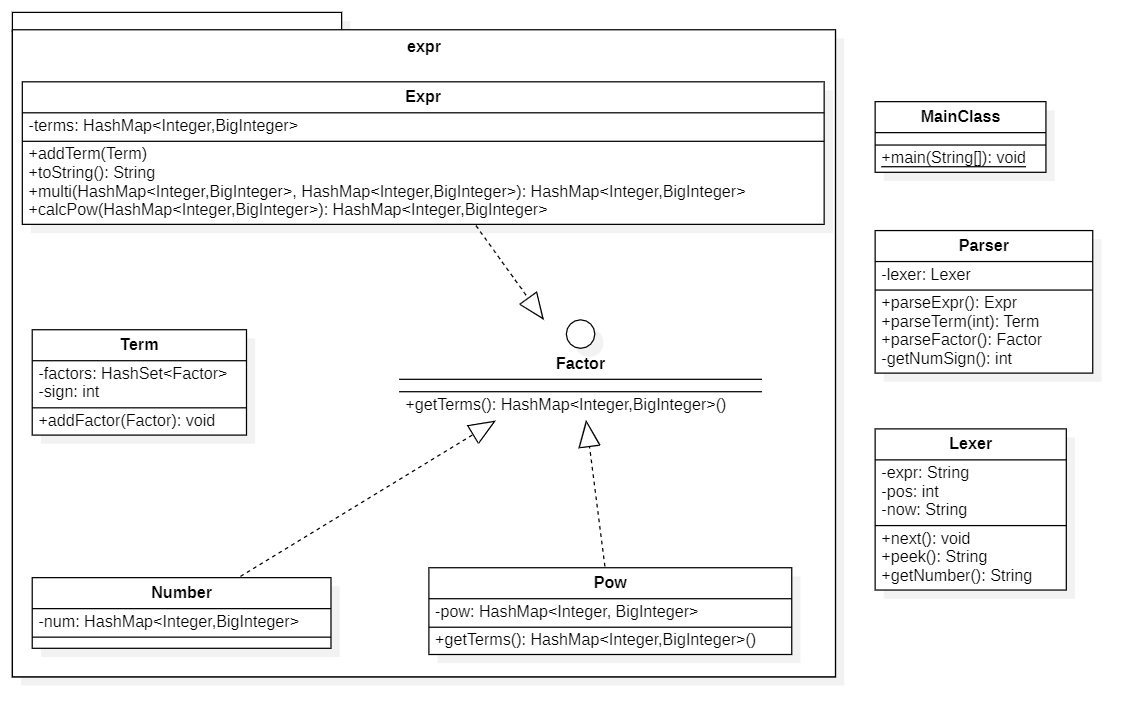
(类图只体现了实现,而没有画出依赖,关联等关系)
-
Parser和Lexer用于解析表达式字符串并抽象出表达式树结构;
-
expr Package 把表达式,项和不同的因子封装成特定的类,提供容器和化简方法等。
-
对于 Factor,有幂函数因子,数字因子和表达式因子三种类型
-
在第一次作业中不难发现,所有项都可以统一为 ax^b(a\in R,b\ge0) 的形式;
-
所有因子都可以抽象成表达式,容器统一为
HashMap<Integer, BigInteger>,化简方法会更简便; -
我们只需要在
expr类中实现乘法运算,就可以同时实现合并同类项的加法和表达式因子之间的乘法。
-
复杂度分析
量化指标可以为代码的改进提供经验性的思路,但是不一定具有绝对的可行性和实际意义
类复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| expr.Expr | 4 | 11 | 28 |
| Parser | 2.6 | 5 | 13 |
| Lexer | 2.5 | 6 | 10 |
| MainClass | 1 | 1 | 1 |
| expr.Number | 1 | 1 | 2 |
| expr.Pow | 1 | 1 | 3 |
| expr.Term | 1 | 1 | 4 |
-
表达式类有点过于臃肿,存在一定的维护隐患,因为内部还有相应的计算化简方法
-
Parser 和 Lexer 复杂度也较高,可能的原因是存在较多的
if-else。
方法复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| expr.Expr.toString() | 22 | 5 | 10 | 11 |
| Parser.parseFactor() | 8 | 3 | 5 | 5 |
| expr.Expr.addTerm(Term) | 7 | 1 | 6 | 6 |
| expr.Expr.multi(HashMap<Integer, BigInteger>, HashMap<Integer, BigInteger>) | 7 | 1 | 4 | 4 |
| Lexer.next() | 6 | 2 | 7 | 8 |
| Parser.getNumSign() | 3 | 1 | 2 | 3 |
| expr.Expr.calcPow(int) | 3 | 2 | 4 | 4 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Parser.parseExpr() | 1 | 1 | 2 | 2 |
| Parser.parseTerm(int) | 1 | 1 | 2 | 2 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.getTerms() | 0 | 1 | 1 | 1 |
| expr.Expr.setTerms(HashMap<Integer, BigInteger>) | 0 | 1 | 1 | 1 |
| expr.Number.Number(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Number.getTerms() | 0 | 1 | 1 | 1 |
| expr.Pow.Pow() | 0 | 1 | 1 | 1 |
| expr.Pow.addTerms(int) | 0 | 1 | 1 | 1 |
| expr.Pow.getTerms() | 0 | 1 | 1 | 1 |
| expr.Term.Term(int) | 0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.getFactor() | 0 | 1 | 1 | 1 |
| expr.Term.getSign() | 0 | 1 | 1 | 1 |
-
expr.toString的高复杂度是架构带来的必然问题-
因为最终所有的项都抽象成
<Integer, BigInteger>的形式存储,而非在项和因子每一层都提供相应的toString方法
-
优缺点分析
-
优点:采用递归下降解析,代码可扩展性较高;统一因子为 “表达式”,便于存储和化简
-
缺点:
expr类中提供了化简和计算的方法,而并非只提供容器,内聚性较差。
第二次作业
类图
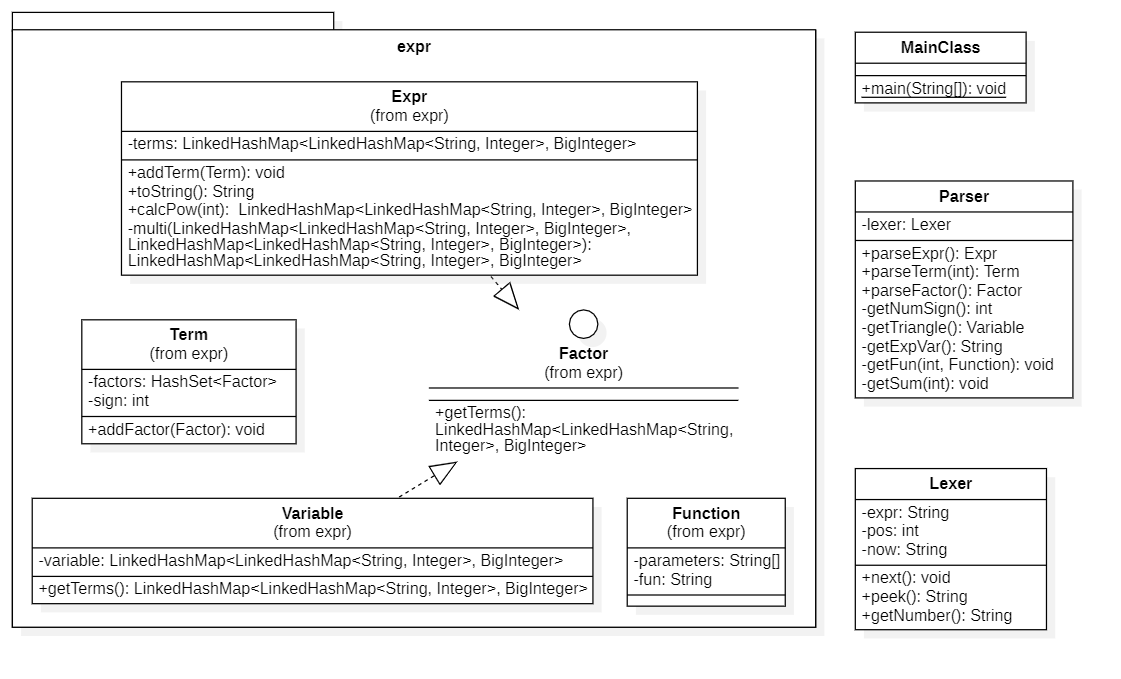
与第一次作业相比:
-
新增自定义函数表达式和求和函数表达式:为了使之前的架构改动尽可能小,采用字符串替换的方法。
-
本质是模拟实参代入函数的过程
-
对于自定义函数:建立
Function类,存储形参列表和原始表达式字符串;Lexer 在读取到函数名时,就对原始自定义函数整体替换。 -
求和函数与上面类似,由于不存在不同函数名,替换原则简单。此处不考虑对其新建类
-
-
新增三角函数因子
-
HashMap<Integer,BigInteger>容器已经不能满足项的复杂性; -
指数作为 key 已经不能表示三角函数,但是指数又是必须要存的;
-
解决办法:采用嵌套
HashMap容器,内部存因子名(x,sin(x**2)等) 和指数,外部用系数作 value -
至此,项和因子已经可以全部统一为嵌套
HashMap的形式(为了顺序一定,使用了LinkedHashMap)
-
-
Lexer 的属性不能使用
final关键字,即可以被修改,便于字符串替换
复杂度分析
绝大多数指标与第三次作业差别不大,统一在 ”第三次作业“ 部分中给出。
bug 修复
-
本次作业中三角函数括号内只包含幂函数因子和常数因子这类单一的简单因子。我的第一反应是利用正则表达式提取括号内的因子
-
然后互测前一天晚上发现,我的正则表达式没有处理常数因子的正负号(
强测居然没测出来?)。比如输入sin(-1)得到sin(1) -
为了尽可能减少修改行数,我采用
BigInteger直接处理
Pattern patternNum = Pattern.compile("(?<num>[+\\-]?\\d+)");
Matcher matcherNum = patternNum.matcher(sb);
if (matcherNum.find()) {
return new BigInteger(matcherNum.group("num")).toString();
}
互测数据
正如研讨课所说,很多人对于底数0和指数0的优化顺序不同,会导致 0^0 型的化简出错。
如 sin(0) ** 0 ,如果先优化 sin(0) 会先得到 0,而先优化指数 0 则无论底数是什么都会得到 1。静态分析互测屋内不同人的代码,使用此样例 hack 到了房间内超过半数的人。
优缺点分析
-
优点:替换后的字符串可以直接调用已经建立好的表达式解析方法,不需要新增函数类实现因子
-
缺点:此次作业中采取正则表达式匹配三角函数内的因子,可扩展性差;正则表达式的细节问题易出现 bug 且较难发现;需要对 Lexer 的属性和方法做较多修改,不太符合开闭原则
第三次作业
类图
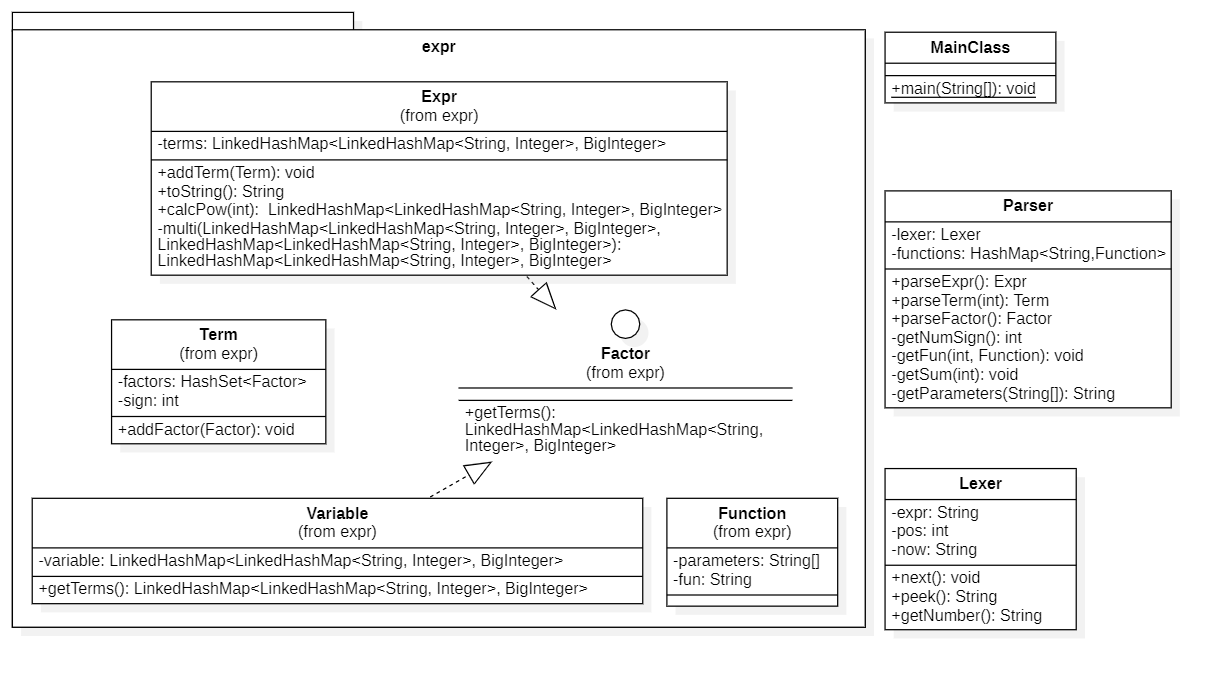
与第二次作业相比:
-
要求可以解决括号嵌套:第一次作业就已经可以解决,但不含三角函数的括号嵌套
-
三角函数允许嵌套因子
-
最基础的做法:满足定义即可,遇到三角函数直接双括号放内部因子。但是性能分可能会很差
-
我选择利用
Parser.parserExpr再次递归下降处理三角函数内部的表达式因子,最终结合expr.toString得到因子名
-
-
允许自定义函数嵌套自定义函数或求和函数:这要求对于实参的提取不能简单的调用
String.split(",")-
新增
Parser.getParameters方法实现实参提取
-
复杂度分析
类复杂度分析
| Class | OCavg | OCmax | WMC |
|---|---|---|---|
| Parser | 5.62 | 13 | 45 |
| expr.Expr | 5.43 | 17 | 38 |
| MainClass | 2 | 2 | 2 |
| Lexer | 1.75 | 6 | 14 |
| expr.Function | 1 | 1 | 3 |
| expr.Term | 1 | 1 | 4 |
| expr.Variable | 1 | 1 | 2 |
-
类的数目很少,部分类复杂度也因此较高
-
Parser 和 Expr 的复杂度成因与第一次作业类似,迭代增量开发导致复杂度又一次升高;
-
对于 MainClass,需要增加自定义函数的读取,复杂度有所增加;
-
喜人的是,我们把多种因子合并成 Variable 类,因子层次的类总复杂度是下降的。
方法复杂度分析
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| expr.Expr.toString() | 38 | 5 | 16 | 18 |
| Parser.getParameters(String[]) | 27 | 1 | 7 | 9 |
| Parser.parseFactor() | 25 | 6 | 13 | 16 |
| expr.Expr.multi(LinkedHashMap<LinkedHashMap<String, Integer>, BigInteger>, LinkedHashMap<LinkedHashMap<String, Integer>, BigInteger>) | 22 | 1 | 8 | 8 |
| Parser.getFun(int, Function) | 12 | 3 | 11 | 12 |
| Parser.getSum(int) | 8 | 1 | 6 | 7 |
| expr.Expr.addTerm(Term) | 7 | 1 | 6 | 6 |
| Lexer.next() | 6 | 2 | 7 | 8 |
| Parser.getNumSign() | 3 | 1 | 2 | 3 |
| expr.Expr.calcPow(int) | 3 | 2 | 4 | 4 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| Parser.parseExpr() | 1 | 1 | 2 | 2 |
| Parser.parseTerm(int) | 1 | 1 | 2 | 2 |
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getExpr() | 0 | 1 | 1 | 1 |
| Lexer.getPos() | 0 | 1 | 1 | 1 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| Lexer.setExpr(String) | 0 | 1 | 1 | 1 |
| Lexer.setPos(int) | 0 | 1 | 1 | 1 |
| Parser.Parser(Lexer, HashMap<String, Function>) | 0 | 1 | 1 | 1 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.getTerms() | 0 | 1 | 1 | 1 |
| expr.Expr.setTerms(LinkedHashMap<LinkedHashMap<String, Integer>, BigInteger>) | 0 | 1 | 1 | 1 |
| expr.Function.Function(String[], String) | 0 | 1 | 1 | 1 |
| expr.Function.getFun() | 0 | 1 | 1 | 1 |
| expr.Function.getParameters() | 0 | 1 | 1 | 1 |
| expr.Term.Term(int) | 0 | 1 | 1 | 1 |
| expr.Term.addFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Term.getFactor() | 0 | 1 | 1 | 1 |
| expr.Term.getSign() | 0 | 1 | 1 | 1 |
| expr.Variable.Variable(String, int, BigInteger) | 0 | 1 | 1 | 1 |
| expr.Variable.getTerms() | 0 | 1 | 1 | 1 |
-
新增
getParameters方法复杂度较高,因为其拥有多层嵌套if-else和循环语句;有存在 bug 的隐患 -
expr.toString虽然复杂度很高,但是实现起来逻辑清晰,肉眼即可优化和 debug
bug 修复
幸亏互测不可以输入自定义函数,不然要被 hack 烂了
Parser.getParameters 对以多元函数为实参的多元函数表达式中实参的提取出现错误
错误样例
1
f(x,y)=(((sin(cos(x))-(+1-sin(cos(y))))))
(f(f(x,x**1),x**+1)*cos(x)**+01)-(cos(sin((x**2))))-(+098782738)**+03
2
f(x,y)=++1-y**+02
g(x,y)=(x**+2-y**02)*(x**02++y**+2)
f(sin(x)**0,cos(x))*sum(i,1,3,(x**2*i)) - (+x*g(sin(x)**+1,f(-0,cos(x))))**1
1
f(x,y)=y-(cos(x)**+3-sin(x)**03)
(f(x**3,f(0,1))-+3*x*sin(x))**2+cos(x)*sum(i,1,5,1)*(+1--cos(x))
均为函数实参含有函数或求和表达式时出现错误。需要合并修复的bug即多元函数嵌套多元函数作为实参时提取实际参数出错
错因
本人采用的是对函数和sum采用直接字符串替换的方式:
-
对于函数表达式:在解析因子时遇到 f,g,h 就替换之后读到的整个函数(用栈思想的括号匹配来确保读取函数的正确性)。而对于参数的分割,本人直接采用了
String[] realParameters = sb.substring(1, sb.length() - 1).split(",");。即用 "," 做分割符得到实际参数。 -
但是,上面方法只对类似作业2中不含函数嵌套的函数表达式因子可以有效处理,如 f(x**3,f(0,1)) 就会分割得到
["x**3", "f(0", "1)"],此处不考虑 f(0,1) 代入,期望得到的结果应该是["x**3","f(0,1)"]。所以对于多元函数嵌套仅采用split方法得不到正确参数,需要结合括号匹配得到正确的函数表达式因子作为实际参数。
互测数据
部分同学代码实现求和函数时,采用了 for(int i = s; i <= e; i++) 或 Integer.parseInt 方法。忽视了 s 和 e 是可以爆 int 的。采用类似sum(i,123456789123456780,123456789123456789,i) 的样例即可 hack
优缺点分析
-
优点:三角函数内因子直接调用已经建立好的递归下降解析方法,降低了思维难度
-
缺点:字符串替换和实参提取的方法略长,为细节维护和 bug 修复带来不便
心得体会
-
Lexer: 词法分析器,在计算机科学中,词法分析,lexing 或标记化是将一系列字符转换成一系列具有指定且因此标识的含义的字符串的过程
-
结合本次作业,Lexer 用于将数字,运算符和括号等语义块提取出来
-
-
Parser: 用于把文本转换成某种数据结构,本质是解码
-
对于本次作业,需要将输入的表达式字符串抽象成表达式树;结合递归下降算法,Parser就可以实现相应的数据结构
-
-
什么是递归下降?
-
表达式 = 表达式 + 项;项 = 项 * 因子;而因子是最小单位
-
上一级调用比自己小一级的自己,越下层模型中形成的优先级越高
-
左递归问题:同等级运算中无法保证优先级
-
解决办法:因子直接只存在乘法运算,可以保证优先级;而项之间的加减运算需要将项和符号分别处理,并把项放入容器中。
-
-
-
测试用例的构造
-
结合代码思路构造:如采用字符串替换,则需要对实参提取方法多做静态分析;如采用新建函数因子类,需要多分析得到因子的方法
-
尽可能尝试边界、极端数据:如多层 sin 嵌套,对于部分同学可能会出现爆栈;如 sum 中采用爆 int, long 的整数,可以 hack 到未采用
BigInteger或BigDemical的代码
-
-
LinkedHashMap-
LinkedHashMap继承自HashMap,在HashMap基础上,通过维护一条双向链表,解决了HashMap不能随时保持遍历顺序和插入顺序一致的问题。
-
-
复杂度分析的概念理解
-
McCabe 复杂度(部分)
-
圈复杂度 v(G) : 用来衡量一个模块的复杂程度
-
基本复杂度 ev(G) : 用来衡量程序非结构化程度
-
设计复杂度 iv(G) : 用来衡量模块之间的调用关系,复杂度越高,模块之间耦合性越高,越难隔离,维护和复用。
-
-
其他复杂度指标
-
认知复杂度 CogC : 一段程序代码被理解的复杂程度,可以等同于代码的理解成本。
-
-
WMC : 类总圈复杂度
-
注:本文未直接复制大段代码,更多的是对架构的描述(直接引入代码可能会影响观感


