【ML基础知识】分类问题常用评价指标
基础概念
通常,我们把分类错误的样本数占总样本数的比例称为“错误率”(error rate),即如果在\(m\)个样本中有\(a\)个样本分类错误,则错误率 \(E=a/m\);相应的,\(1-a/m\) 称为“精度”(accuracy)。
更进一步的,以二分类问题为例,可以将分类结果与实际类别对比用混淆矩阵表示为如下四类:
| reality positives | reality negatives | |
|---|---|---|
| guess positives | True Positives (TP) | False Positives (FP) |
| guess negatives | False Negatives (FN) | True Negatives (TN) |
查准率(Precision,Pre)& 查全率(Recall,Rec)
查准率和查全率是一对矛盾的度量。
查准率表示所有预测为证的样本中,确实为正的比例,即预测精准的比例。(比如买瓜时,使用这个就比较好,宁可放弃一些好瓜,也要保证自己选走的瓜里好瓜的比例尽可能大。极端情况,所有的全猜negative,不买瓜就不会买到坏瓜。)
查准率公式:
查全率表示,所有实际为证的样本中,预测为正的比例,即预测全面的比例。(比如判断生病时,使用这个就比较好,宁可误判一些没有生病的人,也尽量不要漏掉一个确实生病的人。极端情况,所有的全猜positive,把所有人都当成有病,就不会漏掉真正有病的人。)
查全率公式:
一般来说,查准率高时,查全率往往偏低;查全率高时,查准率往往偏低。
很多时候,我们可以根据学习器的预测结果,按照是正例的可能性从大到小对所有样例进行排序,排在前面的是学习器认为“最可能”是正例的样本,排在后面的是学习器认为“最不可能”是正例的样本。按此顺序,把正例数量从0逐渐增加到样本数量n(即从第一种极端情况逐渐增加到第二种极端情况),可以算出每一次的查全率和查准率。以查全率为横轴,查准率为纵轴,可得到查准-查全曲线,简称“P-R曲线”。
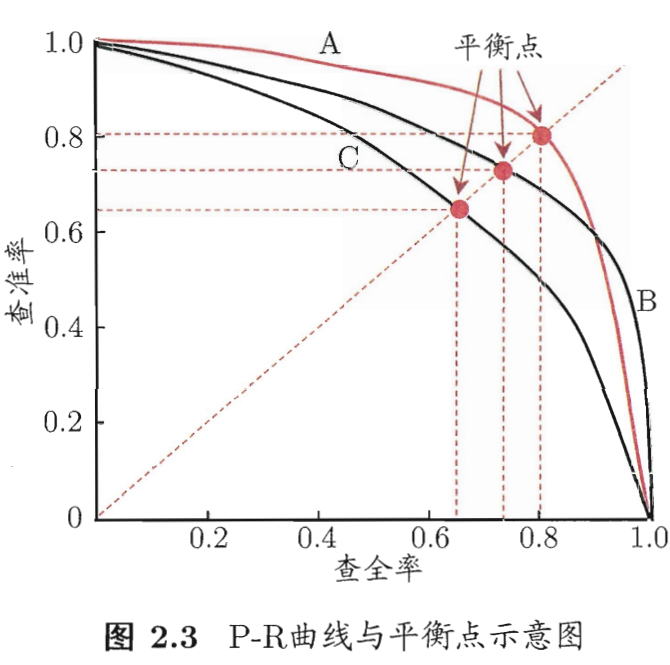
P-R曲线(Precision Recall Curve)
P-R曲线在进行比较时,若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者性能由于前者,如图中学习器A的性能优于学习器C;若两个学习器的P-R曲线有交叉,则难以一般性地断言两者优劣,只能依据具体情况而定。如图中的A与B。
人们综合考虑查准率和查重率的性能,提出了“平衡点”(Break-Event Point, BEP)的概念,平衡点是查准率==查全率时的取值。如上图,依据BEP可认为A学习器优于B学习器。
由于BEP还是过于简化,人们更常用的是F1度量。
F-Score
F-Score又称F-measure,是召回率和准确率的加权调和平均,该指标F引入了系数α对R和P进行加权调和,表达式如下:
其中,\(\alpha>0\) 度量了查全率对查准率的相对重要性。\(\alpha>1\) 时,查全率更重要;\(\alpha<1\) 时查准率更重要;\(\alpha=1\) 时二者一样重要,这种情况就是F1度量,又叫F1-Score。
有时,我们可能会得到多个二分类混淆矩阵,比如进行多次训练或测试时,或再多个数据集上进行训练或测试时,或进行多分类任务,每两两类别组合对比时。因此,我们就希望在 \(n\) 个二分类混淆矩阵上综合考察查准率和查全率。
一种做法是分别在各个混淆矩阵上计算查准率和查全率,记作 \((P_1,R_1),(P_2,R_2),\dots,(P_n,R_n)\) ,再计算平均值,得到“宏查准率”(macro-P)、“宏查全率”(macro-R),再计算出“宏F1”(macro-F1)
另一种做法是先将各混淆矩阵的对应元素进行评价,得到TP,FP,TN,FN的平均值,再依此计算出“微查准率”(micro-P)、“微查全率”(micro-R),再计算出“微F1”(micro-F1)
平均精度(Average Precision,AP)
AP 的精确定义是:Area Under Precision-Recall Curve,即 P-R 曲线下的面积,其公式为:
由于实际工程中,无法得到真实的连续曲线,故需要通过离散的 r 值来计算 AP,可设定一个步长阈值,比如0.01,用101个 p(r) 的平均值来代表 AP 值:
\(P_n\) 表示查全率等于 n 时的查准率值
mean Average Precision(mAP)
mAP 是通过平均类别之间 AP 值,的一种评价指标。即对每一个类别计算其 AP 值,再求所有类别 AP 值的平均即可。
Receiver Operation Characteristic(ROC)
ROC中文叫“受试者工作特征”,类似于P-R曲线,我们将学习器对样本的预测按照正例的可能性大小进行排序,按此顺序逐个把样本预测作正例,计算出两个值,绘制成曲线。不同的是这里计算的两个值不是查准率和查全率,而是“真正例率”(True Positive Rate,TPR)和“假正例率”(False Positive Rate,FPR)。此二者分别定义为:
由公式可知,TPR表示的是,实际为正例的样本,有多少被预测了出来(预测对了)。相应的,FPR表示的是,实际为反例的样本,有多少没有被预测了出来(预测错了)。
显示 ROC 曲线的图像叫做 ROC 图:
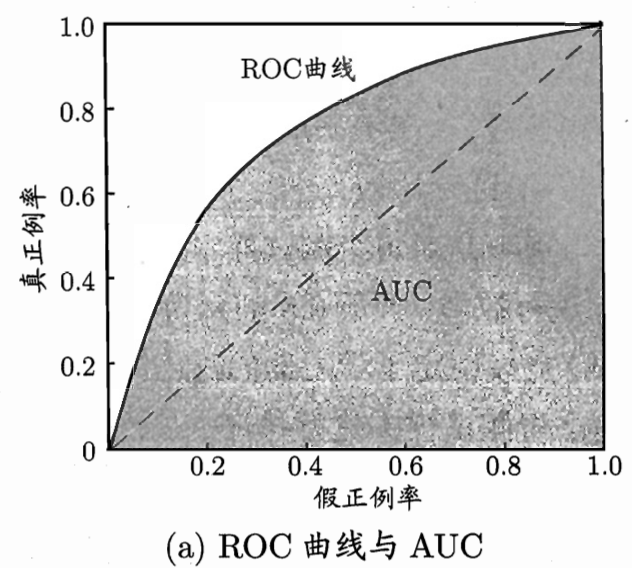
图像中,纵轴表示实际为正的样本被预测为正(预测对)的概率,横轴表示实际为负的样本被预测为正(预测错)的概率。
可知横轴为 0 时代表所有样本都预测成反例,横轴为 1 代表所有样本都预测称正例。
左下到右上的对角线代表正样本预测成正例的概率和负样本预测成正例的概率相等,也就是瞎猜。对角线右下方表示负样本预测成正例的概率大于正样本预测成正例的概率,是反向预测。对角线左上方代表正样本预测成正例的概率大于负样本预测成正例的概率,即有效的学习器。
因此,ROC 曲线越凸向左上方,学习器的性能越好。
类似于 P-R 曲线,如果一个学习器的 ROC 曲线被另一个学习器的曲线完全包围,则可判定后者性能优于前者。若两个学习器 ROC 曲线有交叉,则无法一般性判断优劣,故人们又引入了类似于 AP 概念的 AUC。
Area Under Curve(AUC)
AUC 代表的即是 ROC 曲线下的面积的意思,类似于 AP 代表的是 P-R 曲线下的面积。
和 AP 一样,AUC 也受限于实际工程,无法得到真实的连续曲线,故只能对其面积进行估算,假设 ROC 曲线由坐标 \(\{(x_1,y_1),(x_2,y_2),\dots,(x_m,y_m)\}\) 的点按顺序连接形成的,其中 \((x_1=0,x_m=1)\),如图所示:
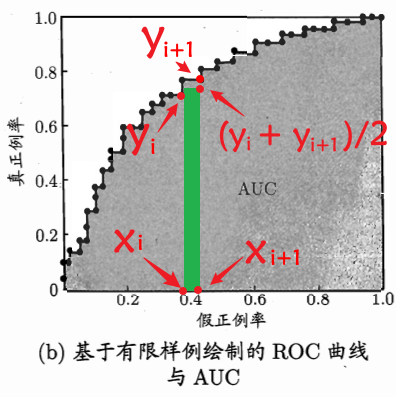
由此,AUC计算公式公式为:
参考:
[1] 周志华.机器学习.[M].清华大学出版社,2016.1



