CF1338D Nested Rubber Bands 题解

首先画几个图玩一下，然后可以发现对答案的贡献是如下这种形式：

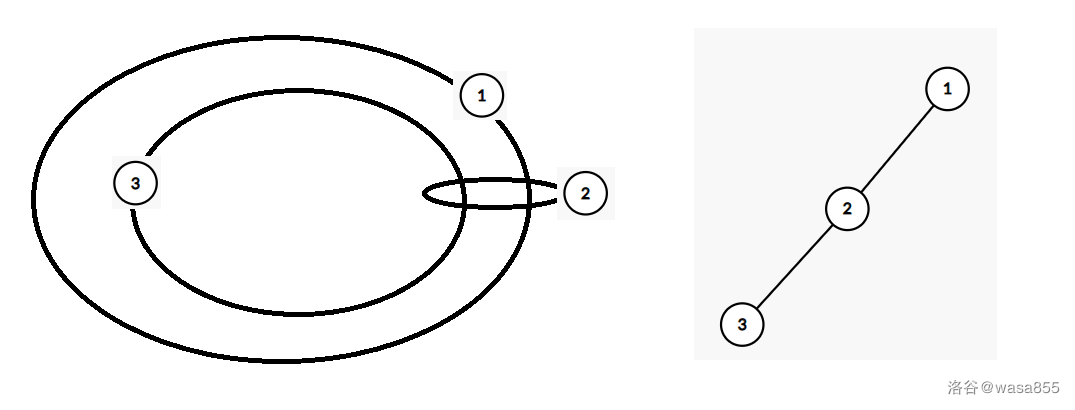
然后再进一步，他还可以是这种形式：

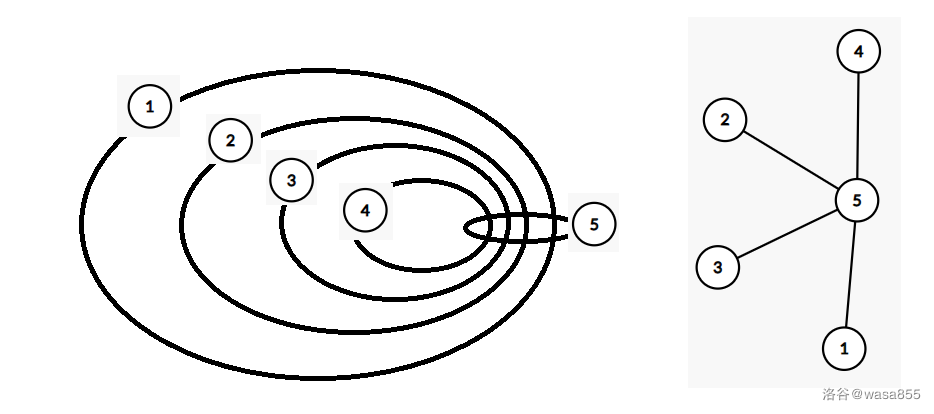
然后你试图把他扩展到一般形式，发现他限制非常多。

例如下图：

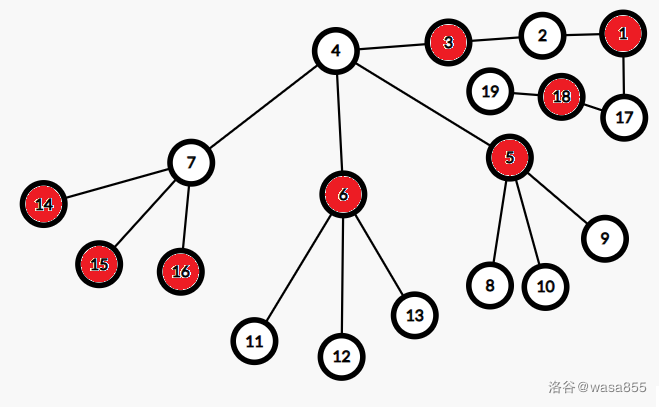
这是他的最优解，注意三个三叉子树只有一个能被完全选入。

原理大概是这样的：

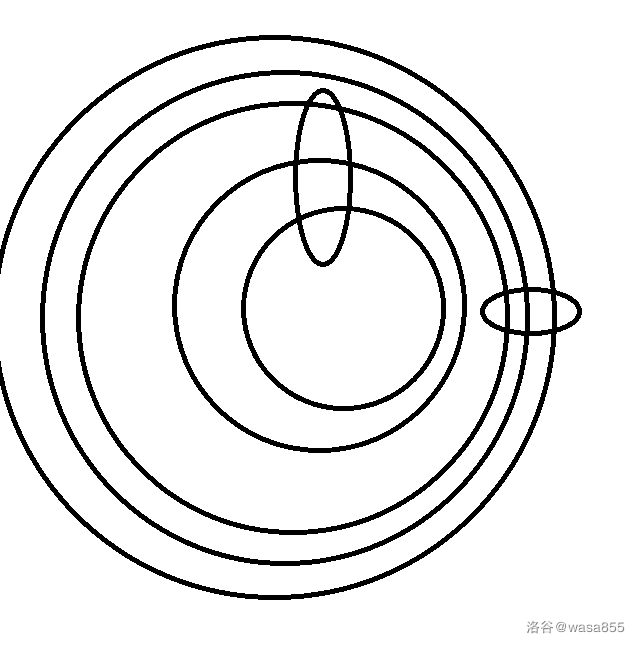
所以一个点只有最多一个子树能被完全计入答案，其他的儿子只有一层有效。

仔细分析一下，发现他答案是找一条链，只保留一级儿子的最大独立集的大小，这个可以通过简单的树形 DP 求出。

---

题解部分讲完了，下面是一些题外话。

这道题我在 cf 的现场已经想到了全部的解法，但是因为一些失误，导致我在一个统计答案的地方少了一个 \(+1\) ，然后他的 pretest 虽然有 \(27\) 个数据点，但没有一个数据点包含了这个细节，于是我 fst 了。而由于前面 A、C 两题的一些高级操作（一场比赛中连着 \(2\) 题没开 long long ，分别贡献了一发罚时），而且由于切题顺序的问题 （\(A\rightarrow C\rightarrow B\)），导致我罚时巨大，最后排在了 rk200+ 的位置。

还好我本来的 rating 很低，所以还是上了一点分，还变成了 IM。

---

这应该是一道好题，他思维难度大，代码难度小（适合我这种不会写代码的人，虽然我还是 fst 了）

Code：

#define N 100005
vector<int> G[N];
bool cmp(int x,int y){return x>y;}
int f[N][2],dep[N],maxd[N],n,ans; // not choose , choose 
void dfs(int u,int fa)
{
	int maxn=0,cnt=0;
	vector<int> a,b,c;
	for(int v:G[u])
	{
		if(v==fa) continue;
		dfs(v,u); cnt++;
		a.pb(f[v][0]);
		b.pb(f[v][1]);
		c.pb(max(f[v][0],f[v][1]));
	}
	sort(a.begin(),a.end(),cmp);
	sort(b.begin(),b.end(),cmp);
	sort(c.begin(),c.end(),cmp);
	if(a.size()==0)
	{
		f[u][1]=1; return ;
	}
	if(a.size()==1)
	{
		f[u][1]=1+a[0];
		f[u][0]=max(a[0],b[0]);
		return ;
	}
	if(u==1)
	{
		int R=cnt-2+c[0]+c[1];
		if(R>ans) ans=R;
		R=a[0]+a[1]+1; // 我少了一个 +1 的地方
		if(R>ans) ans=R;
		f[u][0]=cnt-1+c[0];
		f[u][1]=1+a[0];
	}
	else
	{
		int R=cnt-1+c[0]+c[1];
		if(R>ans) ans=R;
		R=a[0]+a[1]+1; // 还有这里
		if(R>ans) ans=R;
		f[u][0]=cnt-1+c[0];
		f[u][1]=1+a[0];
	}
}
signed main()
{
	cin>>n;
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read();
		G[u].pb(v),G[v].pb(u);
	}
	dfs(1,0);
	cout<<max(ans,max(f[1][0],f[1][1]))<<endl;
	return 0;
}