Longest Palindromic Substring

Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

思路一：

中心扩展法，复杂度O（n^2）

思路二：

动规，复杂度O（n^2）

思路三：

manacher算法，复杂度O(n)。以下为参考资料：

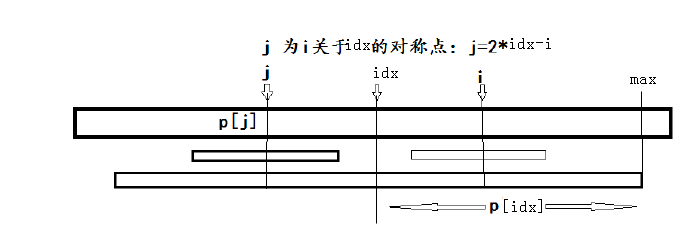
 举例说明：对字符串S=abcdcba而言，最长回文子串是以d为中心，半径为3的子串。当我们采用上面的做法分别求出以S[1]=a, S[2]=b, S[3]=c, S[4]=d为中心的最长回文子串后，对S[5]=c,S[6]=b...还需要一一进行扩展求吗？答案是NO。因为我们已经找到以d为中心，半径为3的回文了，S[5]与S[3]，S[6]与S[2]...，以S[4]为对称中心。因此，在以S[5],S[6]为中心扩展找回文串时，可以利用已经找到的S[3],S[2]的相关信息直接进行一定步长的偏移，这样就减少了比较的次数（回想一下KMP中next数组的思想）。优化的思想找到了，我们先看代码： 

string find_lps_advance(const string &str)
{
    //find radius of all characters
    vector<int> p(str.length(), 0);
    int idx = 1, max = 0;
    for(int i = 1; i < str.length()-1; ++i)
    {
        if(max > i)
        {
            p[i] = p[(idx << 1) - i] < (max - i) ? p[(idx << 1) - i]:(max - i);
        }
        while(str[i+p[i]+1] == str[i-p[i]-1])
            p[i] += 1;
        if(i + p[i] > max)
        {
            idx = i;
            max = i+p[i];
        }
    }

    // find the character which has max radius
    int center = 0, radius = 0;
    for(int i = 0; i < p.size(); ++i)
    {
        if(p[i] > radius)
        {
            center = i;
            radius = p[i];
        }
    }

    return str.substr(center-radius, (radius << 1) + 1);
}

    这里进行简单的解释：上述代码中有三个主要变量，它们代表的意义分别是：

      p:以S[i]为中心的最长回文串的半径为p[i]。

     idx:已经找出的最长回文子串的起始位置。

     max:已经找出的最长回文子串的结束位置。

     算法的主要思想是：先找出所有的p[i]，最大的p[i]即为所求。在求p[j] （j>i）时，利用已经求出的p[i]减少比较次数。

     代码中比较关键的一句是： 

p[i] = p[(idx << 1) - i] < (max - i) ? p[(idx << 1) - i]:(max - i);

    在求p[i]时，如果max>i，则表明已经求出的最长回文中包含了p[i]，那么与p[i]关于idx对称的p[ (idx << 1) - i]的最长回文子串可以提供一定的信息。看了两幅图大概就明白什么意思了：

    求二者的最小值是因为当前能够获取的信息都来自max的左侧，需要进一步比较，求出以S[i]为中心的最长回文串。

    结束行文之前，补充一句，对于字符串类的问题，建议多画一画，寻找其中的规律。

我的代码：

    string longestPalindrome(string s) {
        // IMPORTANT: Please reset any member data you declared, as
        // the same Solution instance will be reused for each test case.
        int n = s.length();
        string ts = "#";
        int len[2*n+1];
        int i, middle = 1, curmax = 2, start = 1, res = 1;
        for(i = 0; i < n; i++){
            ts += s[i];
            ts += '#';
        }
        memset(len, 0, sizeof(len));
        len[1] = 1;
        for(i = 2; i < 2*n+1; i++){
            if(curmax >= i){
                len[i] = len[middle*2-i]<(curmax-i)?len[middle*2-i]:(curmax-i);
            }
            while(i+len[i] < 2*n+1 && ts[i+len[i]] == ts[i-len[i]]){
                len[i]++;
            }
            len[i]--;
            if(i+len[i] > curmax){
                curmax = i+len[i];
                middle = i;
            }
            if(len[i] > res){
                res = len[i];
                start = i;
            }
        }
        ts = ts.substr(start-res, res*2+1);
        i = 0;
        s = "";
        while(ts[i] != '\0')
        {
            if(ts[i] != '#')
                s += ts[i];
            i++;
        }
        return s;
    }