OO第一单元总结
OO第一单元总结
一、整体综述和架构分析
-
项目整体包含以下层次:
-
UML类图如下:(具体分析在迭代过程中描述)
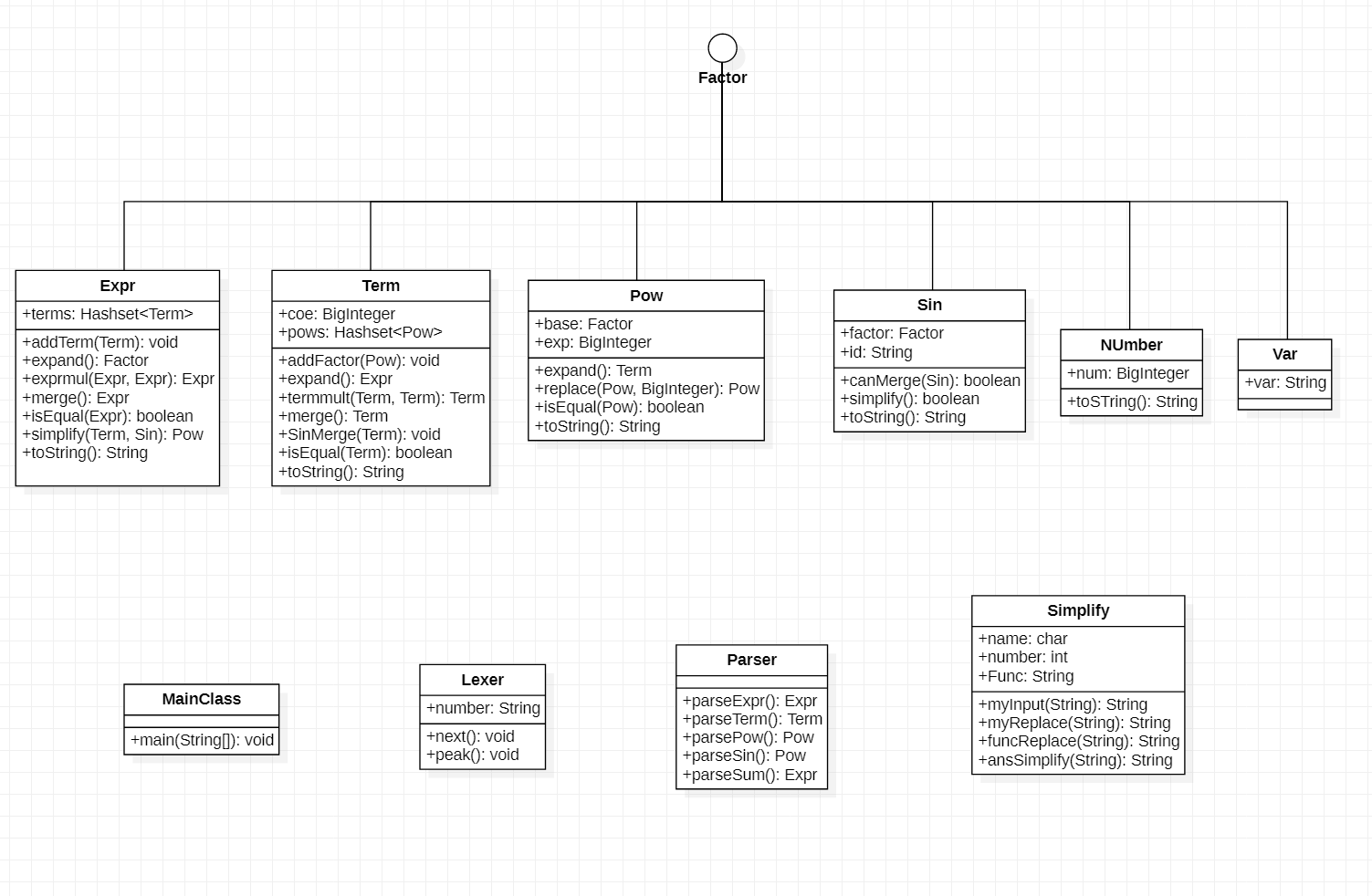
- 代码复杂度分析如下:
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| Lexer.Lexer(String) | 0 | 1 | 1 | 1 |
| Lexer.getNumber() | 2 | 1 | 3 | 3 |
| Lexer.next() | 18 | 2 | 11 | 15 |
| Lexer.peek() | 0 | 1 | 1 | 1 |
| MainClass.main(String[]) | 1 | 1 | 2 | 2 |
| Parser.Parser(Lexer) | 0 | 1 | 1 | 1 |
| Parser.parseExpr() | 7 | 1 | 7 | 7 |
| Parser.parsePow() | 20 | 5 | 13 | 13 |
| Parser.parseSin() | 3 | 1 | 3 | 3 |
| Parser.parseSum() | 5 | 1 | 6 | 6 |
| Parser.parseTerm(BigInteger) | 1 | 1 | 2 | 2 |
| Simplify.Simplify() | 0 | 1 | 1 | 1 |
| Simplify.Simplify(String) | 3 | 1 | 4 | 4 |
| Simplify.ansSimplify(String) | 3 | 1 | 3 | 3 |
| Simplify.funcReplace(String) | 37 | 12 | 21 | 21 |
| Simplify.getName() | 0 | 1 | 1 | 1 |
| Simplify.myInput(String, ArrayList<Simplify>) | 35 | 8 | 8 | 11 |
| Simplify.myReplace(String) | 0 | 1 | 1 | 1 |
| expr.Expr.Expr() | 0 | 1 | 1 | 1 |
| expr.Expr.addTerm(Term) | 0 | 1 | 1 | 1 |
| expr.Expr.expand() | 6 | 1 | 4 | 4 |
| expr.Expr.exprmul(Expr, Expr) | 3 | 1 | 3 | 3 |
| expr.Expr.getTerms() | 0 | 1 | 1 | 1 |
| expr.Expr.isEqual(Expr) | 10 | 4 | 4 | 7 |
| expr.Expr.merge() | 20 | 5 | 10 | 10 |
| expr.Expr.simplify(Term, Sin) | 53 | 11 | 15 | 16 |
| expr.Expr.toString() | 35 | 2 | 18 | 18 |
| expr.Number.Number(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Number.getNum() | 0 | 1 | 1 | 1 |
| expr.Number.setNum(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Number.toString() | 0 | 1 | 1 | 1 |
| expr.Pow.Pow(Factor, BigInteger) | 0 | 1 | 1 | 1 |
| expr.Pow.expand() | 3 | 1 | 3 | 3 |
| expr.Pow.getBase() | 0 | 1 | 1 | 1 |
| expr.Pow.getExp() | 0 | 1 | 1 | 1 |
| expr.Pow.isEqual(Pow) | 23 | 12 | 7 | 17 |
| expr.Pow.replace(Pow, BigInteger) | 12 | 1 | 9 | 9 |
| expr.Pow.setBase(Factor) | 0 | 1 | 1 | 1 |
| expr.Pow.setExp(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Pow.toString() | 17 | 1 | 9 | 9 |
| expr.Sin.Sin(Factor, String) | 0 | 1 | 1 | 1 |
| expr.Sin.canMerge(Sin) | 2 | 2 | 2 | 3 |
| 0 | 1 | 1 | 1 | |
| expr.Sin.getId() | 0 | 1 | 1 | 1 |
| expr.Sin.setFactor(Factor) | 0 | 1 | 1 | 1 |
| expr.Sin.simplify() | 6 | 4 | 3 | 4 |
| expr.Sin.toString() | 7 | 1 | 5 | 5 |
| expr.Term.Term(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Term.addFactor(Pow) | 0 | 1 | 1 | 1 |
| expr.Term.expand() | 40 | 1 | 16 | 16 |
| expr.Term.getCoe() | 0 | 1 | 1 | 1 |
| expr.Term.getPows() | 0 | 1 | 1 | 1 |
| expr.Term.isEqual(Term) | 9 | 4 | 3 | 6 |
| expr.Term.merge() | 35 | 1 | 14 | 15 |
| expr.Term.setCoe(BigInteger) | 0 | 1 | 1 | 1 |
| expr.Term.sinMerge(Term) | 33 | 1 | 13 | 13 |
| expr.Term.termmult(Term, Term) | 2 | 1 | 3 | 3 |
| expr.Term.toString() | 1 | 1 | 2 | 2 |
| expr.Var.Var(String) | 0 | 1 | 1 | 1 |
| expr.Var.getVar() | 0 | 1 | 1 | 1 |
| expr.Var.setVar(String) | 0 | 1 | 1 | 1 |
| Class | OCavg | OCmax | WMC | |
| Lexer | 4 | 12 | 16 | |
| MainClass | 2 | 2 | 2 | |
| Parser | 4.83 | 11 | 29 | |
| Simplify | 5.14 | 17 | 36 | |
| expr.Expr | 6 | 14 | 54 | |
| expr.Number | 1 | 1 | 4 | |
| expr.Pow | 4.11 | 12 | 37 | |
| expr.Sin | 2 | 4 | 14 | |
| expr.Term | 4.73 | 15 | 52 | |
| expr.Var | 1 | 1 | 3 | |
| Package | v(G)avg | v(G)tot | ||
| 5.33 | 96 | |||
| expr | 4.35 | 187 | ||
| Module | v(G)avg | v(G)tot | ||
| Unit1_hw1 | 4.64 | 283 | ||
| Project | v(G)avg | v(G)tot | ||
| project | 4.64 | 283 |
二、作业分析
1. 第一次作业
-
第一次作业可以说是写的最艰辛的,一方面仅仅凭借pre的知识还不足以写出具备一定规模的代码,还需要继续深入学习,另一方面对于递归下降法缺乏了解,不知道从何处下手。在完成了课程组布置的训练环节后才对递归下降法有初步的认识,也照葫芦画瓢的仿照着完成了Lexer和Parser部分的书写。
-
在第一次作业中我建立了Factor接口,Expr类,Term类,Number类,Var类以及Pow类,其中Pow由
Factor Base以及BigInteger exp组成,Base可以是Number、Var、Expr类,exp为他们的幂次。至此表达式树的整体架构完成,通过Lexer和Parser的解析,我们已经构建出一棵表达式树,剩余的工作在于如何进行去括号以及化简。 -
去括号的过程是第一次作业中面临的最严峻的挑战,由于递归下降适合处理嵌套的特性,虽然第一次作业并未要求对嵌套括号进行处理,但本着开发的迭代性和扩展性,在这一过程我决定一步处理到位。在仔细思考后想到表达式树的递归性,也基于递归实现了去括号的过程。
Expr层次:对每一项进行去括号,然后将新项加入Hashset,得到新表达式
Term层次:由于Term由因子组成,而数字因子和幂函数因子可以直接合并,所以在这一层次我把这两种因子先处理好,并将数字因子乘到项的系数中(方便处理) ,同时如果遍历时遇到表达式因子就进入因子层次的化简,最后项由数字因子,幂函数和表达式因子组成,此时尚未化简结束,需要将这些因子乘开,在这里我又写了表达式乘法和项乘法,注意此时Term化简的结果会变成表达式,在这里我是把这一表达式中的每一项加回了上一层的表达式中,这样也就实现了表达式树由深度向广度的转化
Pow层次:在这一层次实现了对表达式因子的化简,首先对其Base调用Expr的去括 号方法(构成递归的循环),然后对高次项进行降次。
通过上述三层次的循环调用,最终实现了表达式去括号操作,我也更深刻的理解如何构建出正确的递归循环,而更复杂的过程则交给程序递归调用去完成。我欣喜的发现最终的表达式树结构十分简洁,仅由表达式,项以及因子三层次构成,也再次验证了方法选择的正确性,为后续迭代开发打下了良好的基础(
指不需要重构) -
最后是同类项的合并,由于此时表达式树结构极其简单仅有三个层次,第三层次仅由数字和幂函数构成因此,只需要在表达式层次调用项合并方法,项层次只需要把因子数化到最简即可。表达式层次把每次合并后的新项与当前已有项对比,如果可以合并则系数合并,无法合并则在表达式中添加新项。至此表达式化简完成。
-
第一次作业历时几天,在缓慢的构思中艰难地完成了,同时为后续开发留下了足够的扩展空间。
2. 第二次作业
-
第二次作业相比第一次作业增加了嵌套括号的处理,同时新增了三角函数因子,自定义函数因子,以及求和函数因子。由于第一次作业中已经实现了嵌套括号的处理,所以只需要对新增因子进行增量开发;
-
因子的增量开发:
-
对于三角函数因子,我建立了三角函数类,并通过标识符区分sin和cos,从而降低重复的代码量;
-
对于求和函数,把求和因子读入以后我选择了递归下降法来替换,即递归的遍历每一层次,如果当前层次是需要替换的i(已设置成Var类),便将其替换,最终返回一个表达式类型,并封装成表达式因子。
-
对于自定义函数,最初我也想类似于求和函数来处理,但实现难度明显提升,因此最终我选择了用字符串替换的方式来实现。虽然字符串替换可能出现各种问题,但是如果填上足量的括号就可以避免这一问题,不过当然这会牺牲一些空间和性能。
-
-
化简:
化简和第一次的思路一样,但这次明显更加复杂,得益于良好架构,第一次作业的每个叶节点只会是数字或幂函数,因此十分容易判断是否为同类项,而本次作业中每一项的因子个数显著增加,由于使用Hashset作为容器,判断相等有两种方式,一种是重写equals和hashcode方法(各因子层也都重写)使其能够自动判断,但会引发x**2与x**2的hashcode值相等,无法加入到Hashset中,由于不想过多改动(
想偷懒)于是便手写了判断是否为同类项的方法。在本次作业中并未实现三角函数的化简。 -
第二次作业实现过程中也为第三次作业预留好了迭代空间,只需要简单从字符串层面处理嵌套函数即可。
3. 第三次作业
-
第三周是相对而言比较轻松的一周,仅在顶层完善了自定义函数的嵌套替换功能便完成了作业 的增量要求,因此在本次作业中我添加了一些简单的三角函数化简,不过仅针对了二次项,并可以识别替换sin(x)**2和替换cos(x)**2那种情况更优。但没有对于高次项的裂次优化,也没有加二倍角优化,部分点性能分可能会受影响。
三、Bug分析与修复
1. 自己遇到的Bug
-
第一次作业在处理连续正负号时考虑不周,由于因子也可以有正负,没有解析
解决:替换掉连续的正负号
-
第二次作业忘记了sum上下限的前导+号,导致RE
-
第三次作业则是化简出现问题,正项放在最前面的优化我直接找到了第一个正项进行字符串替换,结果出现了这样的问题:
2. Hack
-
使用过程中hack到自己的数据
-
测试的边界条件
-
嫖到的自动测试程序
四、心得体会
对于oo的学习大概从假期的pre作业就开始了,简单总结来说算得上是学习过程是"痛苦"的,但进步同样也是飞快的。从最初由于不了解getter和setter用法,不知道多态机制和接口用法,代码的书写进行不下去,到如今已完成初具规模的表达式化简工程,回头来看也仅仅过去了一个月的时间,或许正是在这种“痛苦”中才会收获迅速的成长。




