基于TensorFlow构建CNN识别MNIST数字

本文为博主原创，未经允许，请勿转载：https://www.cnblogs.com/warren2123/articles/11823690.html

一、前言

本文基于Google的TensorFlow框架，实现卷积神经网络的构建，并对MNIST手写数据进行识别。卷积神经网络不同于全连接神经网络之处，在于卷积神经网络是以卷积层、池化层能够保存图片的空间结构，以至于更好的提取图片的信息。下图是CNN的常见架构。

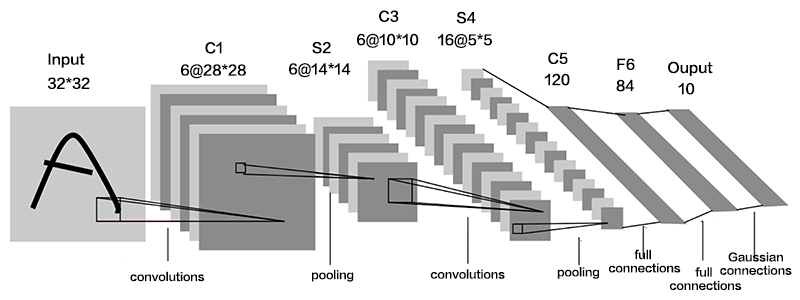
二、基于TensorFlow构建CNN

由于TensorFlow基于静态图计算，所以需要在训练之前，定义数据的计算逻辑。本文采用的卷积神经网络分为四个部分：数据读取及预处理、定义CNN架构、定义模型评估方法、参数优化及保存Session状态。

1、数据读取及预处理

基于TensorFlow内部封装的MNIST处理函数，可以省去数据预处理的步骤。首先导入所需模块，本文采用ONE-HOT的方法对MNIST数据进行处理：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('mnist/', one_hot=True)

2、定义CNN架构

常见的卷积神经网络采用卷积层-池化层代替全连接层，通过深度学习加深即层数的增加，模型会学到的更加抽象的特征，由一开始的轮廓、边缘到后面的具体特征，如一张鸟图片的眼睛、羽毛、爪子。本文采用如下图所示的CNN架构，即两层卷积-池化层、全连接层、输出层的设定，采用不同卷积层、池化层的卷积神经网络会得到不同的效果的提升，由于CNN中的池化层采用下采样的方法，随着层数的增加，会导致数据维度越来越小，以至于后面无法进行学习，当然可以用运用填充的方法来防止，但是合理的结构能够让模型学到更多的信息。

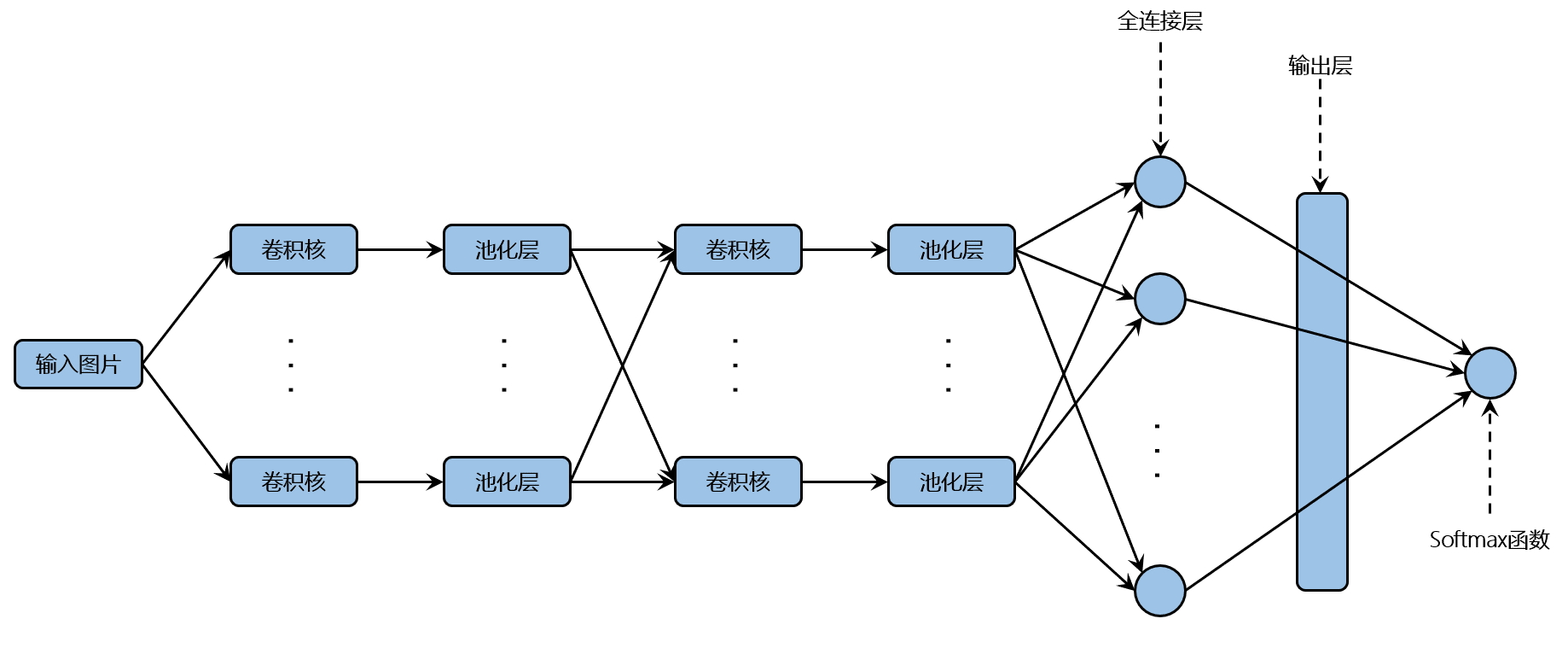
第一个卷积-池化层采用32个滤波器，首先定义输入图片的数据类型，并将图片转化成28x28的数据维度；再以正态分布的形式生成滤波器权重，卷积运算中数据填充以padding='SAME'（用0来填充数据）的方式；最后将偏置设置为常数0.1，以RELU的激活函数生成卷积运算的结果，并运用最大值池化运算方法处理结果，同样采用padding='SAME'填充数据。

num_filters1 = 32

x = tf.placeholder(tf.float32, [None, 784])
x_image = tf.reshape(x, [-1, 28, 28, 1])

W_conv1 = tf.Variable(tf.truncated_normal([5, 5, 1, num_filters1],
                                          stddev=0.1))
h_conv1 = tf.nn.conv2d(x_image, W_conv1,
                       strides=[1, 1, 1, 1], padding='SAME')

b_conv1 = tf.Variable(tf.constant(0.1, shape=[num_filters1]))
h_conv1_cutoff = tf.nn.relu(h_conv1 + b_conv1)

h_pool1 = tf.nn.max_pool(h_conv1_cutoff, ksize=[1, 2, 2, 1],
                         strides=[1, 2, 2, 1], padding='SAME')

第二个卷积-池化层的结构同第一个卷积-池化层，不同之处在于，这层的卷积运算的滤波器采用了64个，虽然采用更大的个数，网络能够学到更加复杂的表示，但是网络的计算代价也会相应变大，而且可能会导致学到不好的模式。更多的滤波器数量，将会在后面输入展开变成更为庞大的神经节点数量，相应的不利于结果输出。

num_filters2 = 64

W_conv2 = tf.Variable(tf.truncated_normal([5, 5, num_filters1, num_filters2],
                                          stddev=0.1))
h_conv2 = tf.nn.conv2d(h_pool1, W_conv2,
                       strides=[1, 1, 1, 1], padding='SAME')

b_conv2 = tf.Variable(tf.constant(0.1, shape=[num_filters2]))
h_conv2_cutoff = tf.nn.relu(h_conv2 + b_conv2)

h_pool2 = tf.nn.max_pool(h_conv2_cutoff, ksize=[1, 2, 2, 1],
                         strides=[1, 2, 2, 1], padding='SAME')

在靠近输出层采用全连接层的方法，便于结果的输出。全连接层的隐藏层采用1024个节点数，运用RELU激活函数输出全连接层的结果，由于神经节点的个数过多，为了防止过拟合的问题，本文采用dropout的方法，随机删除一部分输出结果，以keep_prob指定删除比例；输出层对删除后的输出结果运用softmax运算进行分类输出最终的分类结果。

h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*num_filters2])

num_units1 = 7*7*num_filters2
num_units2 = 1024

w2 = tf.Variable(tf.truncated_normal([num_units1, num_units2]))
b2 = tf.Variable(tf.constant(0.1, shape=[num_units2]))
hidden2 = tf.nn.relu(tf.matmul(h_pool2_flat, w2) + b2)

keep_prob = tf.placeholder(tf.float32)
hidden2_drop = tf.nn.dropout(hidden2, keep_prob)

w0 = tf.Variable(tf.zeros([num_units2, 10]))
b0 = tf.Variable(tf.zeros([10]))
p = tf.nn.softmax(tf.matmul(hidden2_drop, w0) + b0)

3、定义模型评估方法

模型评估方法，本文采用的是交叉熵构建模型的损失函数，进一步运用Adam优化器来优化损失函数，从而是损失函数最小化，最后通过比较预测结果与实际结果的值，计算模型的正确率。

t = tf.placeholder(tf.float32, [None, 10])
loss = -tf.reduce_sum(t * tf.log(p))
train_step = tf.train.AdamOptimizer(0.0001).minimize(loss)
correct_prediction = tf.equal(tf.argmax(p, 1), tf.argmax(t, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

4、参数优化及保存Session状态

在TensorFlow中，需要以会话的形式运行定义好的运算逻辑，通过tf.initialize_all_variables()初始化所有的参数变量，以Saver的方法保存会话的状态结果。

sess = tf.InteractiveSession()
sess.run(tf.initialize_all_variables())
saver = tf.train.Saver()

以下开始训练模型，并且每隔500步输出模型的训练结果，并且保存当前的Session状态。

i = 0
for _ in range(20000):
    i += 1
    batch_xs, batch_ts = mnist.train.next_batch(50)
    sess.run(train_step, feed_dict={x: batch_xs, t: batch_ts, keep_prob: 0.5})
    if i % 500 == 0:
        loss_vals, acc_vals = [], []
        for c in range(4):
            start = int(len(mnist.test.labels) / 4 * c)
            end = int(len(mnist.test.labels) / 4 * (c + 1))
            loss_val, acc_val = sess.run([loss, accuracy], feed_dict={x: mnist.test.images[start:end],
                                                                      t: mnist.test.labels[start:end],
                                                                      keep_prob: 1.0})
            loss_vals.append(loss_val)
            acc_vals.append(acc_val)
        loss_val = np.sum(loss_vals)
        acc_val = np.mean(acc_vals)
        print('Step: %d, Loss: %f, Accuracy: %f' % (i, loss_val, acc_val))
        saver.save(sess, 'cnn_saver/cnn_session', global_step=i)

结果输出：

Step: 500, Loss: 758.870483, Accuracy: 0.975800
Step: 1000, Loss: 603.224609, Accuracy: 0.980800
Step: 1500, Loss: 631.231445, Accuracy: 0.978500
Step: 2000, Loss: 555.882202, Accuracy: 0.982100
Step: 2500, Loss: 472.893158, Accuracy: 0.983200
Step: 3000, Loss: 480.979309, Accuracy: 0.983900
Step: 3500, Loss: 428.443542, Accuracy: 0.984400
Step: 4000, Loss: 406.586060, Accuracy: 0.986100
Step: 4500, Loss: 412.786865, Accuracy: 0.985500
Step: 5000, Loss: 356.059875, Accuracy: 0.987900
Step: 5500, Loss: 350.016785, Accuracy: 0.987800
Step: 6000, Loss: 337.329803, Accuracy: 0.988400
Step: 6500, Loss: 343.874481, Accuracy: 0.988700
Step: 7000, Loss: 381.686676, Accuracy: 0.987800
Step: 7500, Loss: 312.961060, Accuracy: 0.989800
Step: 8000, Loss: 311.136597, Accuracy: 0.989700
Step: 8500, Loss: 363.137939, Accuracy: 0.988700
Step: 9000, Loss: 314.010193, Accuracy: 0.989400
Step: 9500, Loss: 308.214844, Accuracy: 0.990000
Step: 10000, Loss: 276.438904, Accuracy: 0.991100
Step: 10500, Loss: 289.147461, Accuracy: 0.990400
Step: 11000, Loss: 286.594818, Accuracy: 0.990100
Step: 11500, Loss: 274.478912, Accuracy: 0.990600
Step: 12000, Loss: 285.450226, Accuracy: 0.990600
Step: 12500, Loss: 293.722290, Accuracy: 0.990000
Step: 13000, Loss: 273.534210, Accuracy: 0.990900
Step: 13500, Loss: 271.267395, Accuracy: 0.990600
Step: 14000, Loss: 249.533752, Accuracy: 0.991800
Step: 14500, Loss: 263.804474, Accuracy: 0.991300
Step: 15000, Loss: 276.219482, Accuracy: 0.991600
Step: 15500, Loss: 261.917389, Accuracy: 0.990900
Step: 16000, Loss: 278.651794, Accuracy: 0.990800
Step: 16500, Loss: 281.461060, Accuracy: 0.991600
Step: 17000, Loss: 276.703888, Accuracy: 0.990500
Step: 17500, Loss: 281.994995, Accuracy: 0.990600
Step: 18000, Loss: 275.596344, Accuracy: 0.991300
Step: 18500, Loss: 273.061768, Accuracy: 0.991100
Step: 19000, Loss: 254.112183, Accuracy: 0.991900
Step: 19500, Loss: 267.361786, Accuracy: 0.991400
Step: 20000, Loss: 280.701630, Accuracy: 0.991700

三、总结

本文基于TensorFlow构建的卷积神经网络模型，最后得到99.17%的识别精度。如果尝试得到更高的准确率，可以尝试更复杂的CNN架构，以及对应的超参数尝试。下面图形展示的是利用上述优化的模型识别新的手写数字，如尝试写入的3数字，相应的结果展示，以及卷积层的输出展示。

p_val = sess.run(p, feed_dict={x: [image], keep_prob:1.0})

print("我猜你写的是：%s" % (str(np.argmax(p_val))))

fig = plt.figure(figsize=(4, 2))
pred = p_val[0]
subplot = fig.add_subplot(1, 1, 1)
subplot.set_xticks(range(10))
subplot.set_xlim(-0.5, 9.5)
subplot.set_ylim(0, 1)
subplot.bar(range(10), pred, align='center')

我猜你写的是：3

第一层卷积层的输出可视化如下所示：

第二层卷积层的输出可视化如下所示：

posted @ 2019-11-09 14:33 如缕清风阅读(616) 评论(0) 编辑收藏举报

刷新页面返回顶部

如缕清风

——时间如缕，清风拂面。

基于TensorFlow构建CNN识别MNIST数字

一、前言

二、基于TensorFlow构建CNN

三、总结

公告