关于满减优惠券叠加的背包算法
昨天同事遇到一个优惠券使用的问题,用下班时间和早上研究了下,和动态规划的背包问题有关,但又不同于背包,感觉比较有意思就在这里做个记录,在群里讨论和梳理成文字也使自己更清晰的了解自己知道什么。
问题描述
问题的精简描述为:购买商品时,有多张满减优惠券可用(可叠加使用),求最优策略(减免最多)。 准确描述为:
设共有n张优惠券C: [(V1, D1), (V2, D2), (V3, D3), ..., (Vn, Dn)],其中Vn为面值,Dn为减免值(对于一张优惠券Cx,满Vx减Dx),优惠券为单张,可叠加使用(使用过一张后,如果满足面值还可以使用其他优惠券)。求商品价值为M时,使用优惠券的最优策略:1.减免值最多,2.优惠券剩余最优(比如对于 C1 (2, 0.1) 、C2 (1, 0.1) 只能选择一张的最优取舍就是用C1留C2 )。
输入:
C = [(2, 1.9), (1, 1), (1, 0.1), (2, 0.1)] , M = 3
期望输出:
使用优惠券:[(2, 0.1), (2,1.9), (1,1)]
总减免:3
看到其他人推荐背包,由于没用过背包算法,通过 动态算法规划算法背包问题 学习了下背包的思想。顺便了解一下动态规划能解决什么问题:
适用动态规划方法求解的最优化问题应该具备的两个要素:最优子结构和子问题重叠。——《算法导论》动态规划原理
优惠券问题看起来和背包问题很像,但是有一点不同
一点不同
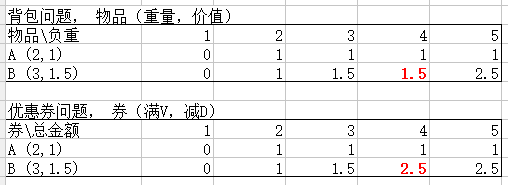
图1 背包问题和优惠券问题的不同
图中,背包问题里面的数据为:在负重已知的前提下能装物品的最优总价值;优惠券问题里面的数据为总金额能使用优惠券的最优总减免值。
对于背包问题,如果负重为4,策略只能是拿2号物品,因为拿取2号之后负重还剩(4-3=1),再拿不了1号物品了(最终价值为1.5);对于优惠券问题,如果金额为4,使用完2号优惠券之后,金额还剩(4-1.5=2.5),还可以再用1号优惠券的(最终减免值为2.5)。
总结这个不同就是:背包判断大于重量W,再减去W,得到剩余值再去上一层找最优解(统计价值);优惠券则是需要判断大于面额V,再减去减免值D,剩余值再去上一层找最优解(统计减免值D)。
而且因为这个不同,优惠券问题的数据对优惠券顺序是有要求的,不像背包问题中,总是负重减物品重量,剩余的重量直接去找上次最优再计算就好了。顺序问题分两种:
两种顺序
一、对于优惠券,不同面额的顺序
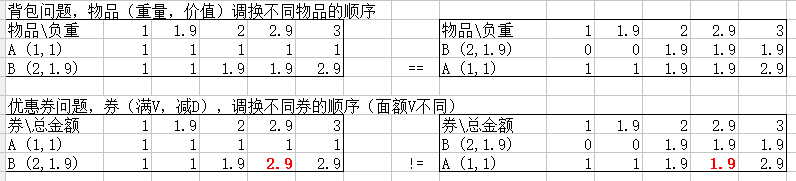
图2 优惠券面额顺序对结果的影响
图中,将物品和券的顺序颠倒,对于背包问题,最后一行数据完全相同,对结果无影响;对于优惠券问题,顺序变了结果会不一样。(因为需要满足优惠券(v,d), 中的v才能减去第二项,所以对顺序有要求)。所以,不同面额 (V不同) 的优惠券,应该升序排列。
二、面额相同,减免值不同

图3 优惠券面额相同,不同减免值的顺序对结果的影响
因为背包思想是通过上一次的结果来铺垫下一次的值,所以从上往下需要先生成同额度的最优值。所以,同面额不同减免值 (V同D不同) 的优惠券,应该降序排列。
排序示例为:
[
(2, 1.9),
(1, 1),
(1, 0.1),
(2, 0.1)
]
需排列为
[
(1, 1),
(1, 0.1),
(2, 1.9),
(2, 0.1),
]
综以上 一点不同两种顺序 的情况所述,使用背包之前需要排序(V升D降),按V升序,如果V相同,再按D降序排。再使用背包算法(大于V减去D)。
还没有优化的程序
本来想说一句,思路有了,程序都不重要。但是,在写的过程中,这个排序思路(V升D降),是试出来的,而不是先想好的。所以动手还是很重要的,不然我的脑子还想不长远。
用的多维数组,可以优化的点有:用一维数组存储;间隔优化(如果优惠券有分,span为100,那数组就很大了)。Python 版程序:
# coding:utf-8
# 背包算法,解决满减优惠券叠加使用问题
def coupon_bags(coupon, amount):
"""
优惠券背包算法
param: coupon 优惠券数组
param: amount 金额
"""
# 转换金额跨度(间隔): 元->角
span = 10
amount = int(amount*span)
for i, v in enumerate(coupon):
for j in range(len(v)):
coupon[i][j] = int(coupon[i][j]*span)
# 初始化结果数组,dps 存储满减值(背包算法结果) ,dps_coupons 存储优惠券
dps = []
dps_coupons = []
for i in range(len(coupon)+1):
dps.append(list((0,)*(amount+1)))
# list 直接 * 生成的是同一list,用循环生成
dps_coupons.append([])
for j in range(amount+1):
dps_coupons[i].append([])
for i in range(1, len(coupon)+1):
for j in range(1, amount+1):
if j < coupon[i-1][0]:
# 获取上个策略值
dps[i][j] = dps[i-1][j]
dps_coupons[i][j] = dps_coupons[i-1][j]
else:
if(dps[i-1][j] > dps[i-1][j-coupon[i-1][1]]+coupon[i-1][1]):
# 上一行同列数据 优于 当前优惠券+剩余的金额对应的上次数据,取之前数据
dps[i][j] = dps[i-1][j]
dps_coupons[i][j] = dps_coupons[i-1][j]
else:
# 选取当前+剩余 优于 上一行数据
dps[i][j] = dps[i-1][j-coupon[i-1][1]]+coupon[i-1][1]
dps_coupons[i][j] = dps_coupons[i-1][j-coupon[i-1][1]].copy()
dps_coupons[i][j].insert(0, tuple(coupon[i-1]))
# print(f"{i} {j}, {tuple(coupon[i-1])} dps {i-1} {j-coupon[i-1][1]}:{dps_coupons[i-1][j-coupon[i-1][1]]} ")
print('----------------------------------------------------')
# 结果需返回数据原单位(元)
result_coupons = dps_coupons[-1][-1].copy()
for i, v in enumerate(result_coupons):
result_coupons[i] = list(result_coupons[i])
for j in range(len(v)):
result_coupons[i][j] = result_coupons[i][j]/span
print(f"使用优惠券:{result_coupons} 总减免:{dps[-1][-1]/span}")
# 优惠券
coupon_items = [
[1, 1],
[1, 0.1],
[2, 1.9],
[2, 0.1],
]
# 举例中的优惠券是最终顺序。确保优惠券已经排序过,多维升序(V升D降),此处省略
# sorted_coupon(coupon)
coupon_bags(coupon_items, 3)
"""
coupon_items = [
[1, 0.6],
[2, 0.7],
[2, 1.3],
[3, 2.3],
]
coupon_bags(coupon_items, 5)
"""
输出:使用优惠券:[[2.0, 0.1], [2.0, 1.9], [1.0, 1.0]] 总减免:3.0
还写了PHP版本的,一并发上来吧。
<?php
/**
* 背包算法,解决优惠券问题
* @param array $coupon 优惠券数组
* @param float $amount 金额
*/
function coupon_bags($coupon, $amount)
{
# 转换金额单位(跨度):角
$span = 10;
$amount = intval($amount * $span);
foreach ($coupon as $i => $v) {
for ($j = 0; $j < count($v); $j++) {
$coupon[$i][$j] = intval($coupon[$i][$j] * $span);
}
}
# 结果,多数组
$dps = [];
$dps_coupons = [];
for ($i = 0; $i <= count($coupon); $i++) {
for ($j = 0; $j <= $amount; $j++) {
$dps[$i][$j] = 0;
$dps_coupons[$i][$j] = [];
}
}
# 排序,多维升序(内降)
# sort_coupon($coupon);
for ($i = 1; $i <= count($coupon); $i++) {
for ($j = 1; $j <= $amount; $j++) {
if ($j < $coupon[$i - 1][0]) {
# 获取上个策略值
$dps[$i][$j] = $dps[$i - 1][$j];
$dps_coupons[$i][$j] = $dps_coupons[$i - 1][$j];
} else {
if ($dps[$i - 1][$j] > $dps[$i - 1][$j - $coupon[$i - 1][1]] + $coupon[$i - 1][1]) {
# 上一行同列数据 优于 当前优惠券+剩余的金额对应的上次数据,取之前数据
$dps[$i][$j] = $dps[$i - 1][$j];
$dps_coupons[$i][$j] = $dps_coupons[$i - 1][$j];
} else {
# 选取当前+剩余 优于 上一行数据
$dps[$i][$j] = $dps[$i - 1][$j - $coupon[$i - 1][1]] + $coupon[$i - 1][1];
$dps_coupons[$i][$j] = $dps_coupons[$i - 1][$j - $coupon[$i - 1][1]];
$dps_coupons[$i][$j][] = $coupon[$i - 1];
}
}
}
}
# 结果需返回数据原单位(元)
$t = end($dps_coupons);
$t2 = end($dps);
$result_coupons = array_reverse(end($t));
$result_dps = end($t2);
foreach($result_coupons as &$v){
foreach($v as &$v2){
$v2 = $v2/$span;
}
}
$result_dps/=$span;
echo "\n使用优惠券:". print_r($result_coupons, true). "总减免:{$result_dps}.";
}
$coupon_items = [
[1, 1],
[1, 0.1],
[2, 1.9],
[2, 0.1],
];
coupon_bags($coupon_items, 3);
Java 版的代码:(粗糙)
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
class CouponTicket{
List<int[]> cp = new LinkedList<int[]>();
public CouponTicket copy(){
CouponTicket r = new CouponTicket();
for(int[] c : cp){
r.cp.add(c);
}
return r;
}
public String toString(){
StringBuilder s = new StringBuilder();
for(int[] c: cp){
s.append(Arrays.toString(c)).append(" - ");
}
return s.toString();
}
}
/**
* 背包算法,解决满减优惠券叠加使用问题
*
*/
public class Coupon{
public static void main(String[] args){
double [][]coupon_items = {
{1, 1},
{1, 0.1},
{2, 1.9},
{2, 0.1},
};
Coupon.couponBags(coupon_items, 3);
}
public static void couponBags(double[][] coupon, double amount){
// 转换成int的金额精度
int span = 10;
int amountInt = (int)(amount*span);
int couponInt[][] = new int[coupon.length][2];
// 初始化结果数组,dps 存储满减值(背包算法结果) ,dps_coupons 存储优惠券
int[][] dps = new int[coupon.length+1][amountInt+1];
CouponTicket[][] dps_coupons = new CouponTicket[coupon.length+1][amountInt+1];
for(int i=0; i<coupon.length; i++){
for(int j=0; j<coupon[i].length; j++){
couponInt[i][j] = (int)(coupon[i][j]*span);
}
}
// 计算
for(int i=1; i<=coupon.length; i++){
for(int j=1; j<=amountInt; j++){
// System.out.printf("%d %d coupon[%d][0]=%s %b " ,i,j,i-1,couponInt[i-1][0], (j<couponInt[i-1][0]));
if(j < couponInt[i-1][0]){
// 获取上个策略值
dps[i][j] = dps[i-1][j];
dps_coupons[i][j] = dps_coupons[i-1][j];
}else{
if(dps[i-1][j] > dps[i-1][j-couponInt[i-1][1]]+couponInt[i-1][1]){
// 上一行同列数据 优于 当前优惠券+剩余的金额对应的上次数据,取之前数据
dps[i][j] = dps[i-1][j];
dps_coupons[i][j] = dps_coupons[i-1][j];
}
else{
if(dps_coupons[i][j] == null){
dps_coupons[i][j] = new CouponTicket();
}
// 选取当前+剩余 优于 上一行数据
dps[i][j] = dps[i-1][j-couponInt[i-1][1]]+couponInt[i-1][1];
if(dps_coupons[i-1][j-couponInt[i-1][1]] != null){
dps_coupons[i][j] = dps_coupons[i-1][j-couponInt[i-1][1]].copy();
}
dps_coupons[i][j].cp.add(couponInt[i-1]);
// System.out.printf("%s dps %d %s", Arrays.toString(couponInt[i-1]), j-couponInt[i-1][1],dps_coupons[i-1][j-couponInt[i-1][1]]);
}
}
// System.out.println();
}
}
System.out.println("优惠券使用和总满减金额如下:(优惠券未转换原金额)");
System.out.println(dps_coupons[coupon.length][amountInt]);
System.out.println(dps[coupon.length][amountInt]/(double)span);
}
}
总结
算法思想很重要。多思考多动手多交流。如果发现了漏洞,请您不吝赐教。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号