POJ 1740

POJ 1740

先手必败状态为 偶数堆且为从小到大排序后(1,2)相等,(3,4)相等...，可以理解为每一堆都有与它对称的一堆
解释：在这种情况下，先手无论什么操作，后手都可以执行对称的操作，从而维持先手必败状态，而且总数量是减少的，所以先手必败

其他状态都是先手必胜状态

如果为奇数堆
解释:先从小到大排序，然后用最大的那一个填平所有(1,2),(3,4)...之间的差距，补完之后多出的部分全拿走。
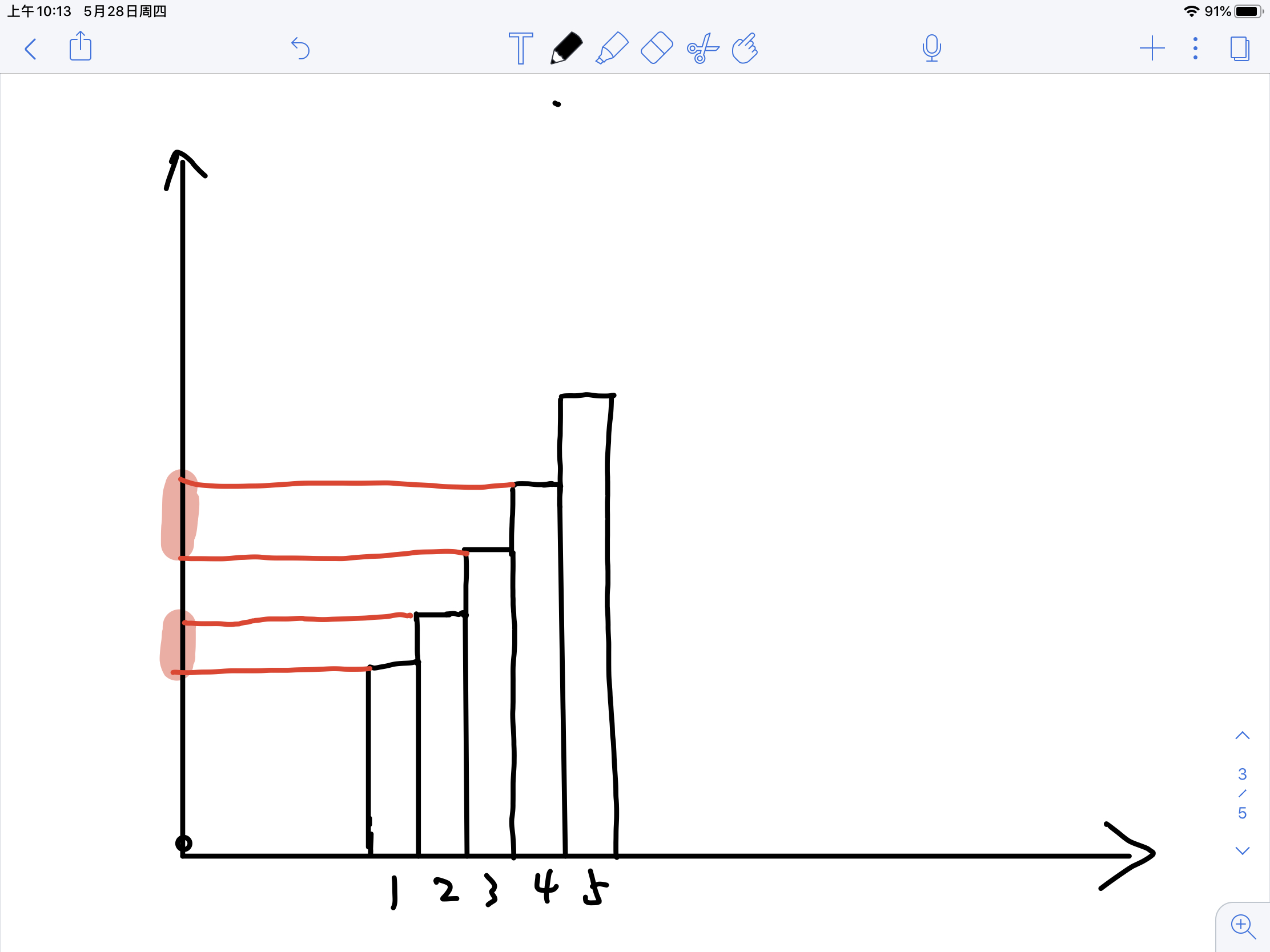
证明能填满：看这个图，红色区间指需要填平的地方，因为已经排序了，所以它们不会重叠，总长度加起来不会超过最大的长度

如果为偶数
解释:先从小到大排序，然后用（最大的-最小的）填平所有(1,2),(3,4)...之间的差距，补完之后多出的部分全拿走。
证明同理。

 

 

#include <bits/stdc++.h>
#define inf 2333333333333333
#define N 1000010
#define p(a) putchar(a)
#define For(i,a,b) for(int i=a;i<=b;++i)

using namespace std;
int n,flag;
int a[N];
void in(int &x){
    int y=1;char c=getchar();x=0;
    while(c<'0'||c>'9'){if(c=='-')y=-1;c=getchar();}
    while(c<='9'&&c>='0'){ x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    x*=y;
}
void o(int x){
    if(x<0){p('-');x=-x;}
    if(x>9)o(x/10);
    p(x%10+'0');
}

signed main(){
    while(cin>>n && n){
        flag=0;
        For(i,1,n) in(a[i]);
        if(n&1){
            o(1);p('\n');
            continue;
        }
        else{
            sort(a+1,a+n+1);
            for(int i=2;i<=n;i+=2)
                if(a[i]!=a[i-1]){
                    flag=1;
                    break;
                }
            if(flag) o(1);
            else o(0);
            p('\n');
        }
    }
    return 0;
}