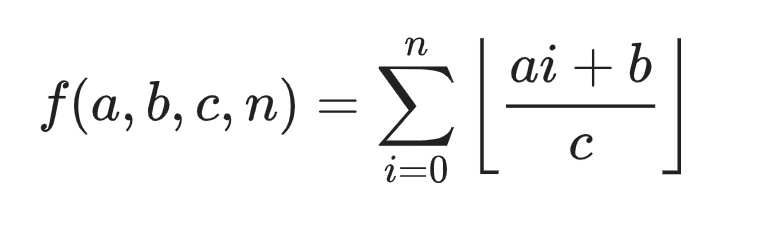
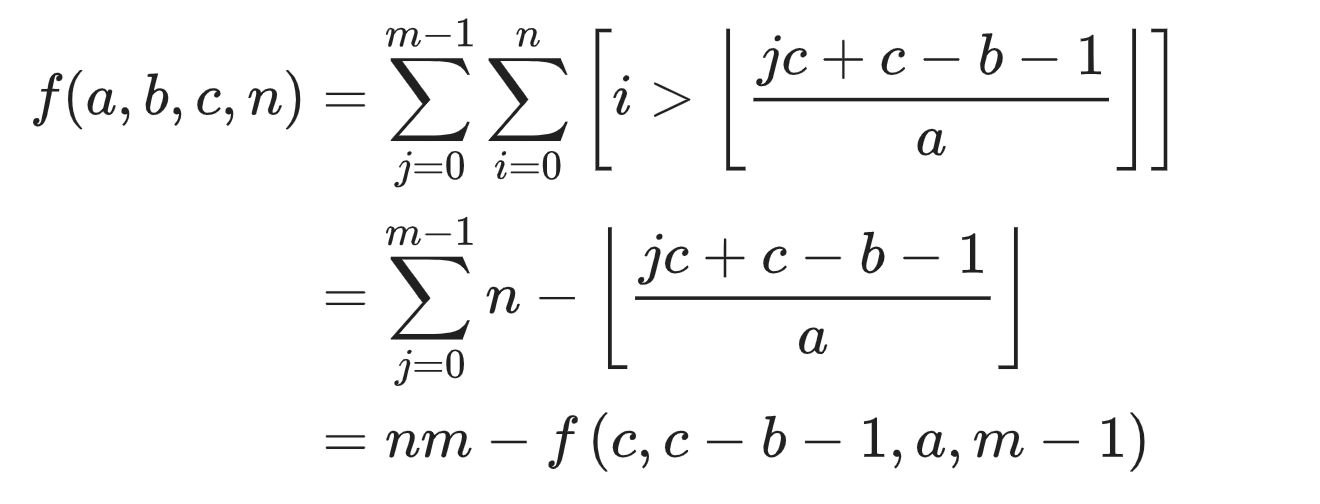
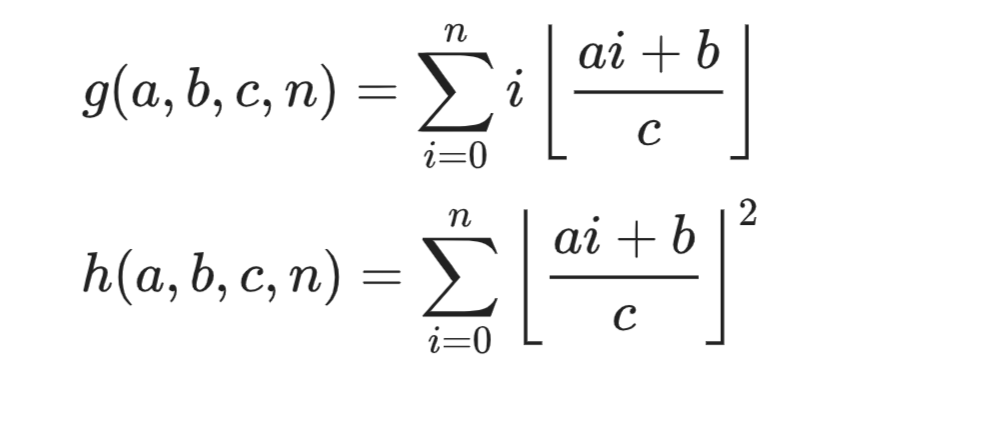
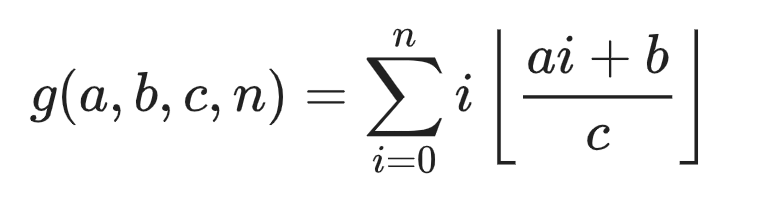
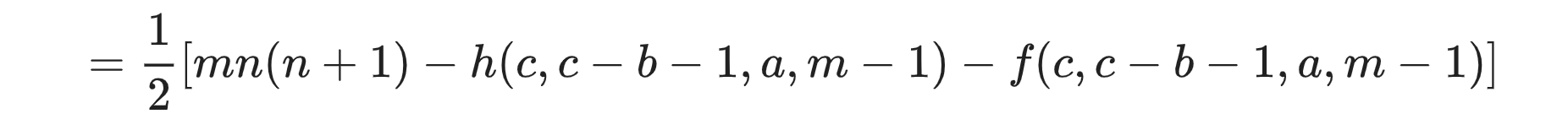
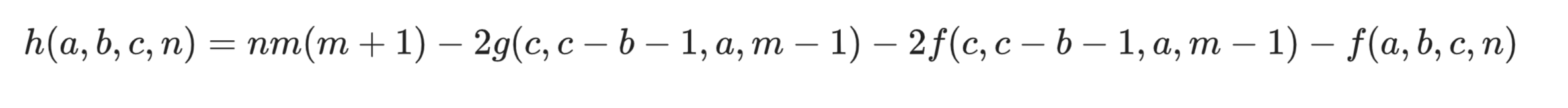
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
#include <cmath>
#include <cstring>
#define inf 2147483647
#define P 998244353
#define p(a) putchar(a)
#define For(i,a,b) for(long long i=a;i<=b;++i)
using namespace std;
long long T;
long long n,a,b,c;
long long i2 = 499122177, i6 = 166374059;//这是2,6在%P意义下的逆元
struct data{
long long f,g,h;
data calc(long long n,long long a,long long b,long long c){
long long ac = a / c, bc = b / c, m = (a * n + b) / c, n1 = n + 1, n21 = n * 2 + 1;
data d;
if (a == 0) {
d.f = bc * n1 % P;
d.g = bc * n % P * n1 % P * i2 % P;
d.h = bc * bc % P * n1 % P;
return d;
}
if (a >= c || b >= c){
d.f = n * n1 % P * i2 % P * ac % P + bc * n1 % P;
d.g = ac * n % P * n1 % P * n21 % P * i6 % P + bc * n % P * n1 % P * i2 % P;
d.h = ac * ac % P * n % P * n1 % P * n21 % P * i6 % P +
bc * bc % P * n1 % P + ac * bc % P * n % P * n1 % P;
d.f %= P, d.g %= P, d.h %= P;
data e = calc(n, a % c, b % c, c);
d.h += e.h + 2 * bc % P * e.f % P + 2 * ac % P * e.g % P;
d.g += e.g, d.f += e.f;
d.f %= P, d.g %= P, d.h %= P;
return d;
}
data e = calc(m - 1, c, c - b - 1, a);
d.f = n * m % P - e.f, d.f = (d.f % P + P) % P;
d.g = m * n % P * n1 % P - e.h - e.f, d.g = (d.g * i2 % P + P) % P;
d.h = n * m % P * (m + 1) % P - 2 * e.g - 2 * e.f - d.f;
d.h = (d.h % P + P) % P;
return d;
}
}ans;
void in(long long &x){
long long y=1;char c=getchar();x=0;
while(c<'0'||c>'9'){if(c=='-')y=-1;c=getchar();}
while(c<='9'&&c>='0'){ x=(x<<1)+(x<<3)+c-'0';c=getchar();}
x*=y;
}
void o(long long x){
if(x<0){p('-');x=-x;}
if(x>9)o(x/10);
p(x%10+'0');
}
signed main(){
in(T);
while(T--){
in(n);in(a);in(b);in(c);
ans=ans.calc(n,a,b,c);
o(ans.f);p(' ');o(ans.h);p(' ');o(ans.g);p('\n');
}
return 0;
}
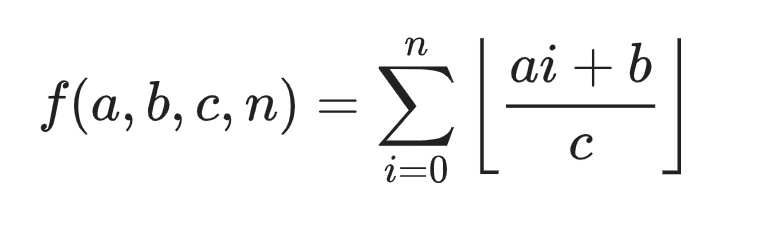
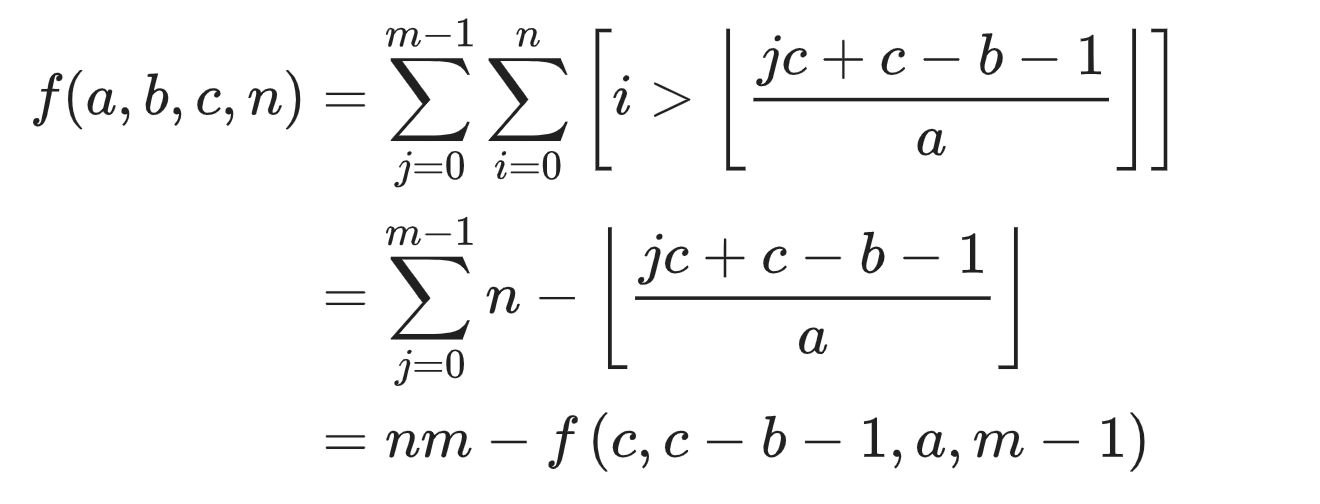


 浙公网安备 33010602011771号
浙公网安备 33010602011771号