poj3233

(g++比c++快不少

分治+矩阵快速幂

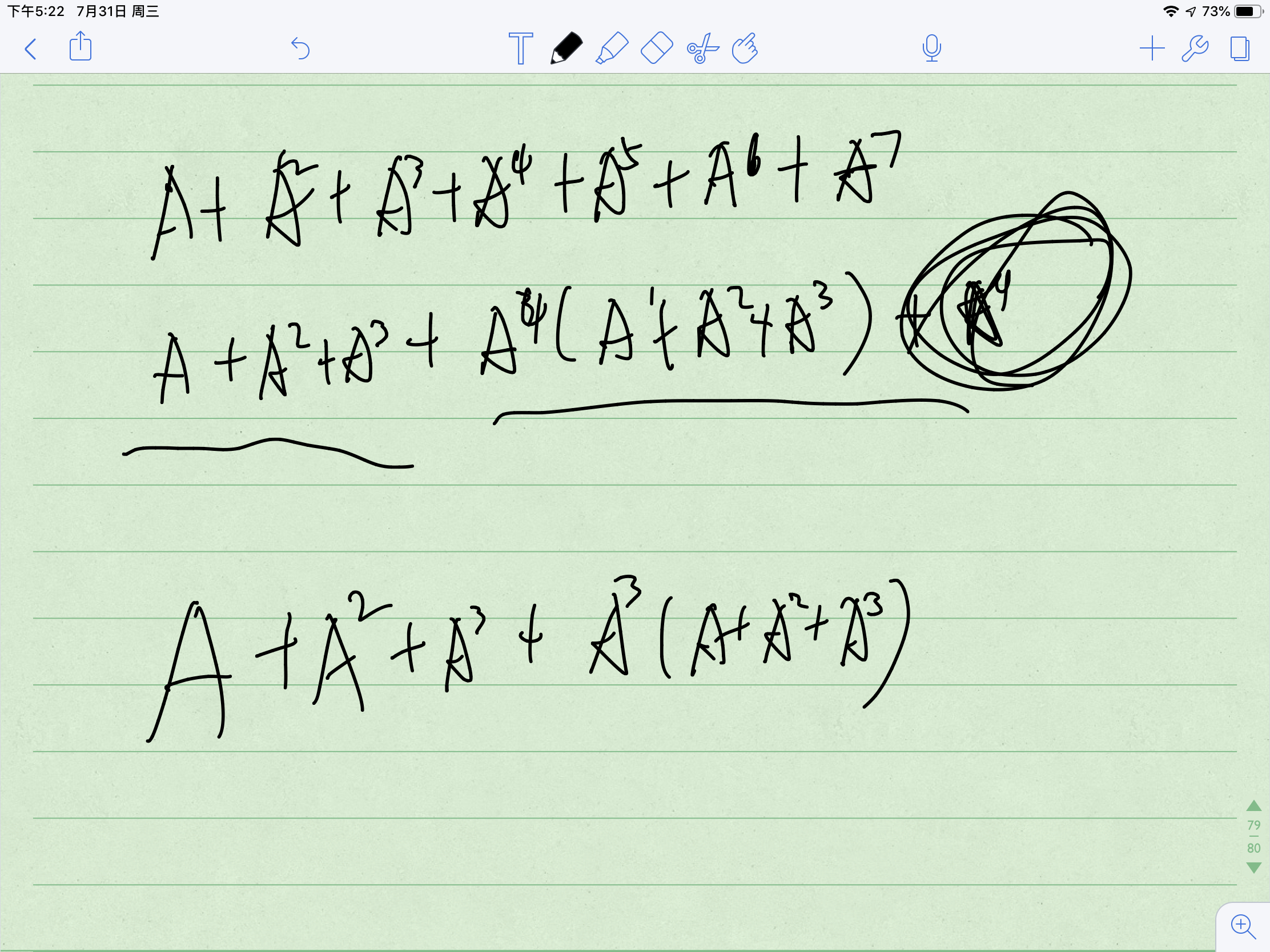
#include<iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<cmath>
#include<cstring>
#define inf 2147483647
#define N 1000010
#define p(a) putchar(a)
#define For(i,a,b) for(register long long i=a;i<=b;++i)

using namespace std;
long long n,k,m;

struct matrix{
    long long a[40][40];
    matrix operator * (const matrix & b) const{
        matrix r;
        For(i,1,n)
            For(j,1,n){
                r.a[i][j]=0;
                For(k,1,n)
                    r.a[i][j]+=a[i][k]*b.a[k][j]%m;
                    r.a[i][j]%=m;
            }
        return r;
    }
}init;

void in(long long &x){
    long long y=1;char c=getchar();x=0;
    while(c<'0'||c>'9'){if(c=='-')y=-1;c=getchar();}
    while(c<='9'&&c>='0'){ x=(x<<1)+(x<<3)+c-'0';c=getchar();}
    x*=y;
}
void o(long long x){
    if(x<0){p('-');x=-x;}
    if(x>9)o(x/10);
    p(x%10+'0');
}

matrix ksm(matrix a,long long k){
    matrix r=a;k--;
    if(k==0)
        return r;
    while(k>0){
        if(k%2==1)
            r=r*a;
        a=a*a;
        k>>=1;
    }
    return r;
}

matrix add(matrix A,matrix B){
    matrix r;
    For(i,1,n)
        For(j,1,n)
            r.a[i][j]=(A.a[i][j]+B.a[i][j])%m;
    return r;
}

matrix sum(matrix a,long long k){
    if(k==1)
        return a;
    matrix half,t,temp;
    half=sum(a,k>>1);
    if(k&1){
        t=ksm(a,(k>>1)+1);
        temp=half*t;
        return add(add(half,temp),t);
    }
    else{
        t=ksm(a,k>>1);
        temp=half*t;
        return add(temp,half);
    }
}

int main(){
    in(n);in(k);in(m);
    For(i,1,n)
        For(j,1,n){
            in(init.a[i][j]);
            init.a[i][j]%=m;
        }
    matrix r;
    r=sum(init,k);
    For(i,1,n){
        For(j,1,n)
            o(r.a[i][j]),p(' ');
        p('\n');
    }
    return 0;
}