软工个人项目作业
| 项目 | 内容 |
|---|---|
| 北航2020软工 | 班级博客 |
| 作业要求 | 个人项目作业 |
| 项目GitHub地址 | 个人项目 |
| 教学班级 | 006 |
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 10 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 270 | 280 |
| · Analysis | · 需求分析 (包括学习新技术) | 20 | 30 |
| · Design Spec | · 生成设计文档 | 10 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 30 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 20 | 20 |
| · Design | · 具体设计 | 30 | 30 |
| · Coding | · 具体编码 | 100 | 80 |
| · Code Review | · 代码复审 | 20 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 50 | 50 |
| Reporting | 报告 | 80 | 90 |
| · Test Report | · 测试报告 | 20 | 20 |
| · Size Measurement | · 计算工作量 | 30 | 40 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 30 |
| 合计 | 360 | 380 |
解题思路
拿到题目后,首先想到的是两两直线组合,因为答案是有限个,只有相交和平行两种情况。
参考https://blog.csdn.net/u010177286/article/details/46226183
每条直线表示为一般式方程\(Ax+By+C=0\)
那么两条直线\(a_0x+b_0y+c_0=0\) 和\(a_1x+b_1y+c_1=0\)
的交点为
\(x=(b_0*c_1-b_1*c_0)/D\)
\(y=(a_1*c_0-a_0*c_1)/D\)
\(D=a_0*b_1-a_1*b_0\)
当D=0时两直线平行
估计复杂度为O(n^2)
注:由于坐标范围为\((-10^5,10^5)\),相乘后可能溢出,因此使用long long。
设计实现
1.class dot:点类
bool dot::operator <(const dot& d)const
重写比较方法
根据坐标判断两点是否重合
2.class line:直线类
dot* line::cross(line l)
求两直线交点,若平行则返回nullpointer
3.class Cross:相交类
long long Cross::getDifCrossDotsNum(vector<line> lines)
计算非重合交点个数
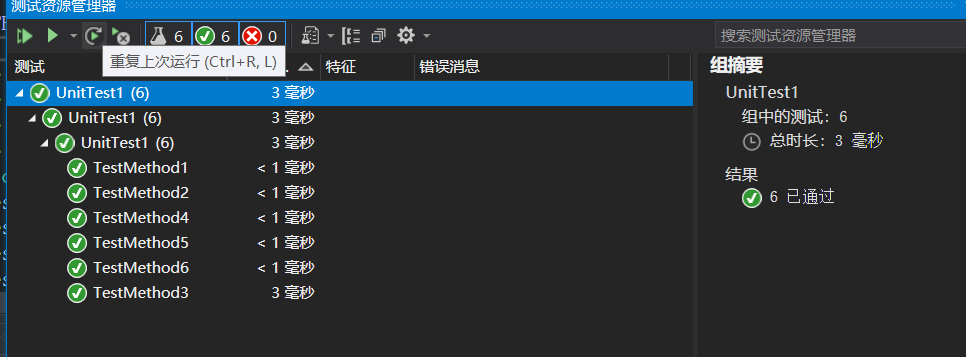
4.单元测试
采用Assert测试了上述三个函数
性能分析
思考了很多想法,都是复杂度为O(n^2),因此没有做过多优化。
性能分析图:
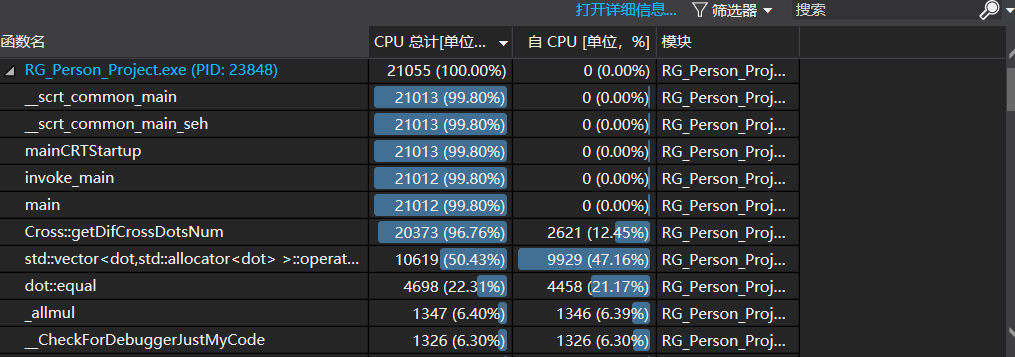
消耗最大的函数为
Cross::getDifCrossDotsNum()
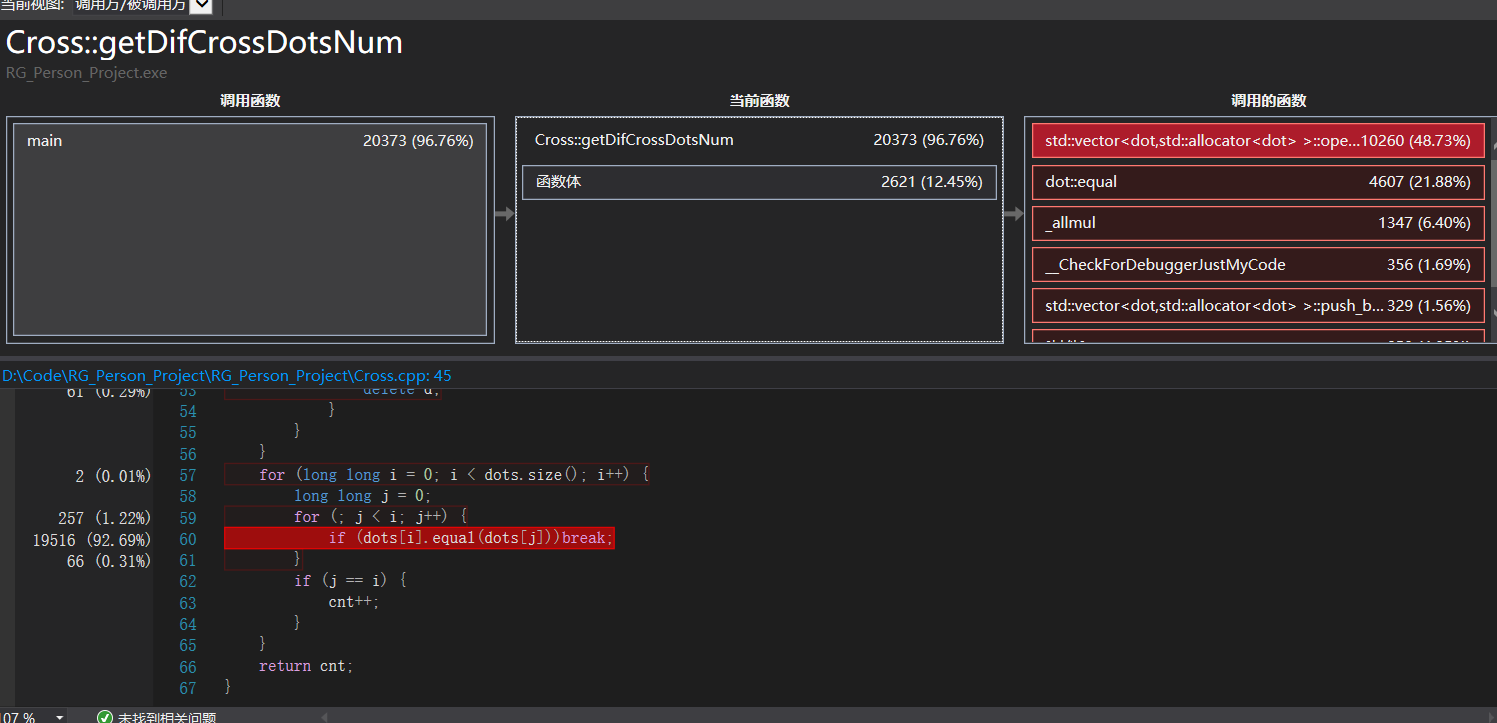
代码说明
bool dot::operator<(const dot& d)const
{
if (x_top * d.x_bottom != x_bottom * d.x_top) {
return x_top * d.x_bottom < x_bottom * d.x_top;
}
else {
return y_top * d.y_bottom < y_bottom * d.y_top;
}
}
因为交点可能是非整数点,因此利用分子分母交叉相乘的方法来判断两点是否重合。
dot* line::cross(line l) {
long long D = A * l.B - B * l.A;
long long x_top = B * l.C - C * l.B;
long long y_top = l.A * C - A * l.C;
dot* cross_dot = NULL;
if (D != 0)cross_dot = new dot(x_top, D, y_top, D);
return cross_dot;
}
根据前面的解题思路,若D==0则平行,返回NULL
否则返回交点的坐标
long long Cross::getDifCrossDotsNum(vector<line> lines)
{
for (unsigned int i = 0; i < lines.size() - 1; i++) {
for (unsigned int j = i + 1; j < lines.size(); j++) {
dot* d = lines[i].cross(lines[j]);
if (d != NULL) {
dots.insert(*d);
delete d;
}
}
}
return dots.size();
}
两两计算交点并存入dots;
TEST_METHOD(TestMethod1)
{
dot* d1 = new dot(1, 2, 1, 2);
dot* d2 = new dot(2, 4, 2, 4);
Assert::IsFalse(d1->operator <(*d2));
}
TEST_METHOD(TestMethod2)
{
line* l1 = new line(100000, 0, 0, 100000);
line* l2 = new line(-100000, 0, 0, -100000);
Assert::IsNull(l1->cross(*l2));
}
TEST_METHOD(TestMethod3)
{
line l1(1, 1, 2, 3);
line l2(2, 3, 4, 5);
line l3(7, 4, 3, 1);
vector<line> lines;
lines.push_back(l1);
lines.push_back(l2);
lines.push_back(l3);
Cross* cross = new Cross();
Assert::AreEqual(cross->getDifCrossDotsNum(lines),long long(3));
}
TEST_METHOD(TestMethod4)
{
line l1(1, 1, 2, 3);
vector<line> lines;
lines.push_back(l1);
Cross* cross = new Cross();
Assert::AreEqual(cross->getDifCrossDotsNum(lines), long long(0));
}
TEST_METHOD(TestMethod5)
{
line l1(1, 0, 1, 3);
line l2(2, 0, 2, 3);
vector<line> lines;
lines.push_back(l1);
lines.push_back(l2);
Cross* cross = new Cross();
Assert::AreEqual(cross->getDifCrossDotsNum(lines), long long(0));
}
TEST_METHOD(TestMethod6)
{
line l1(100000, 0, 0, 100000);
line l2(-100000, 0, 0, 100000);
line l3(-100000, 0, 0, -100000);
line l4(100000, 0, 0, -100000);
vector<line> lines;
lines.push_back(l1);
lines.push_back(l2);
lines.push_back(l3);
lines.push_back(l4);
Cross* cross = new Cross();
Assert::AreEqual(cross->getDifCrossDotsNum(lines), long long(4));
}
}
一部分单元测试代码,测试了三个函数
Code Quality Analysis