[数据结构] 栈

栈的定义及特点

栈（Stack）是只允许在一端进行插入或删除操作的线性表，如图所示：

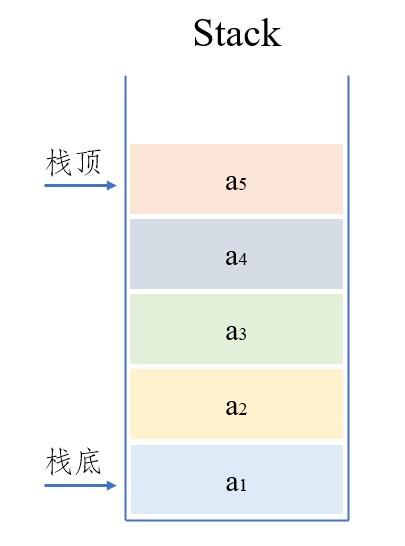
栈顶（top）：线性表允许进行插入、删除的一端；

栈底（bottom）：不允许进行插入和删除的一端；

空栈：不含任何元素的空表。

如上图所示，设某个栈\(S=(a_1, a_2, a_3, a_4, a_5)\)，则\(a_1\)为栈底元素，\(a_5\)为栈顶元素。进栈顺序为\(a_1, a_2, a_3, a_4, a_5\)，出栈顺序为\(a_5, a_4, a_3, a_2, a_1\)，由此可见，栈的操作特性可以明显地概括为先进后出、后进先出

栈的顺序存储

采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时设置一个指针top指示当前栈顶元素的位置

• 结构体

  #define MaxSize 50
  typedef struct {
      int data[MaxSize];
      int top;
  }Stack;
  

  栈顶指针 ：S.top，初始设置为-1；栈顶元素：S->data[S.top]；

  进栈操作：栈不满时，栈顶指针++，再送值到栈顶；

  出栈操作：栈非空时，取栈顶元素，栈顶指针--；

  栈空条件：S.top=-1，栈满条件：S.top==MaxSize - 1，栈长：S.top+1。

  bool StackEmpty(Stack *S) {
      if(S->top == -1)
          return true;
      else
          return false;
  }
  

• 入栈

  首先咱要初始化栈

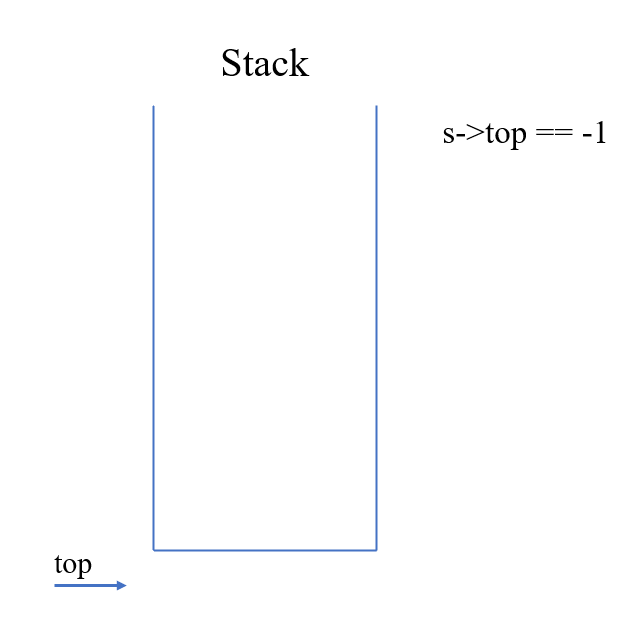
  void InitStack(Stack *s) {
      S->top == -1;
  }
  

  然后咱看图

  这是初始化的情况

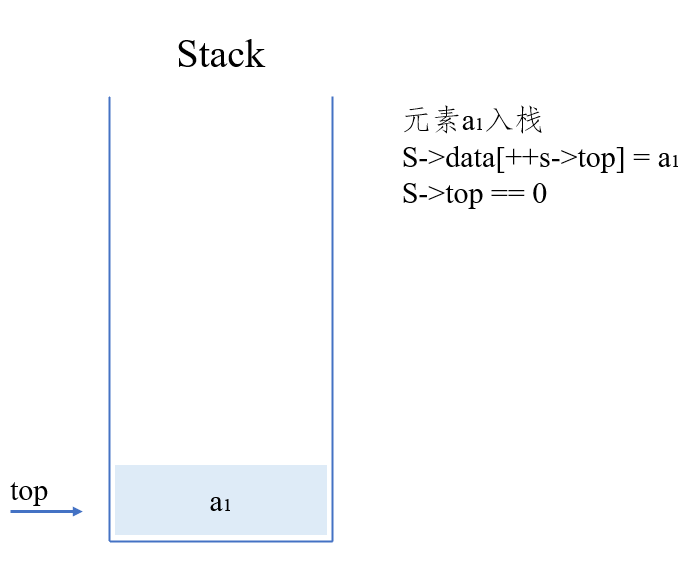
元素\(a_1\)入栈

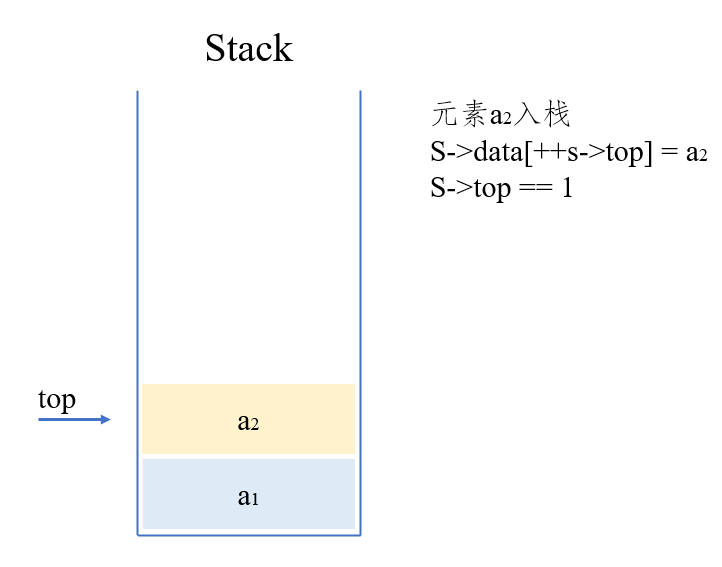
元素\(a_2\)入栈

以此类推

给出代码：

void Push(Stack *S, int x) {
    if(S->top == MaxSize - 1)
        return ; // 栈满
    S->top ++;
    S->data[S->top] = x;
}

• 出栈

  元素\(a_2\)出栈

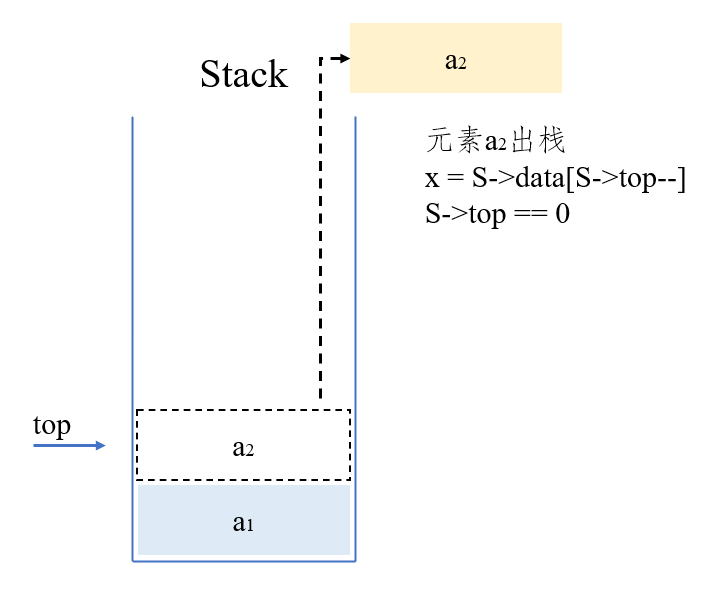
元素\(a_1\)出栈

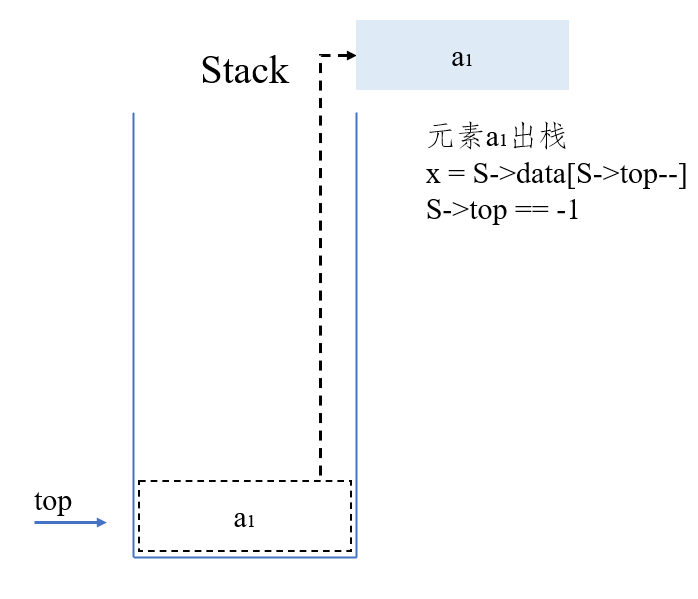
代码：

void Pop(Stack *S, int *x) {
    if(S->top == -1)
        return ; // 栈空
    *x = s->data[S->top --];
}

共享栈

利用栈底位置相对不变的特性，让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，栈顶分别向共享空间的中间延伸，如下图所示：

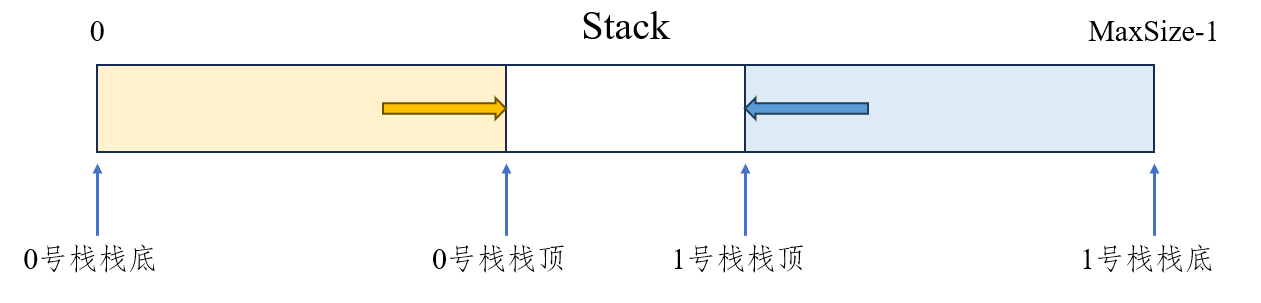
两个栈的栈顶指针都指向栈顶元素，top0 = -1时0号栈为空，top1 = MaxSize - 1时1号栈为空；当且仅当两个栈顶指针相邻（top1 - top0 = 1）时栈满。

共享栈是为了更好有效地利用存储空间，两个栈的空间相互调节，只有在整个存储空间被占满时才会发生上溢。其存取数据的时间复杂度均为O(1)。

链栈

采用链式存储的栈称为链栈，链栈的优点是便于多个栈共享存储空间和提高效率，且不存在栈满上溢的情况。通常采用单链表实现，并且规定所有的操作都是在单链表表头进行。这里规定链栈没有头节点。

下面给出一些基本操作的代码：

• 初始化

  typedef struct StackNode {
      int data; // 数据域
      struct StackNode *next; // 指向下一个节点的指针
  } StackNode;
  
  typedef struct Stack {
      StackNode *top; // 栈顶指针
  } Stack;
  
  void init_stack(Stack *S) {
      S->top = NULL; // 初始化栈顶指针为空，表示栈为空
  }
  

• 判空

  int is_empty(Stack *S) {
      return S->top == NULL; // 如果栈顶指针为空，表示栈为空，返回 1，否则返回 0
  }
  

• 进栈

  void push(Stack *S, int x) {
      StackNode *new_node = (StackNode*)malloc(sizeof(StackNode)); // 创建新结点
      new_node->data = x; // 将数据存入新结点的数据域
      new_node->next = S->top; // 将新结点插入到栈顶之后
      S->top = new_node; // 更新栈顶指针
  }
  

• 出栈

  int pop(Stack *S) {
      if (S->top == NULL) { // 如果栈为空，则输出错误信息并返回
          printf("栈为空\n");
          return -1;
      }
      int x = S->top->data; // 取出栈顶元素
      StackNode *temp = S->top; // 保存栈顶指针
      S->top = S->top->next; // 栈顶指针指向下一个节点
      free(temp); // 释放原栈顶节点的内存
      return x; // 返回栈顶元素
  }
  

写在最后

后续应该还会补充一个完整的代码，敬请等待。