NLP复习之神经网络

NLP复习之神经网络

前言

tips：

• 设计神经网络时，输入层与输出层节点数往往固定，中间层可以自由指定；
• 神经网络中的拓扑与箭头代表预测过程数据流向，与训练的数据流有一定区别；
• 我们不妨重点关注连接线，因为它们是权重，是要训练得到的

神经元

神经元模型是一个包含输入、输出、计算功能的模型，注意中间的箭头线，称之为“连接”，上面有“权值”

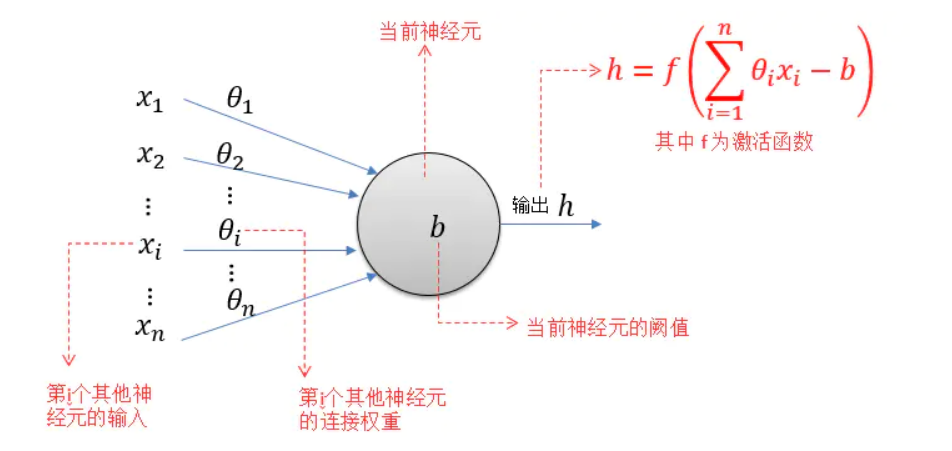
​ 一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。

MP神经元模型接收来自n个其他神经元传递过来的输入信号（x1~xn），这些输入信号通过带权重（θ或ω来表示权重，上图采用θ）的连接（Connection）进行传递，然后神经元（图示阈值为b）收到的总输入（所有输入和权重的乘积的和）与神经元的阈值b比较，并经由激活函数（Activation Function，又称响应函数）处理之后产生神经元的输出。

理想情况下，激活函数的形式应为阶跃函数（也就是修正线性单元ReLU），通常选择Sigmoid函数：

$$Sigmoid(x)=S(x)=\frac{1}{1+e^{-x}}$$

其值域为$(0,1)$。

​ 神经元可以看做一个计算与存储单元，计算是神经元对其的输入进行计算，存储是神经元会暂存计算结果，传递到下一层。

多层神经网络

单层神经网络（感知机）在此处暂时忽略不写，期末要挂科了

上图展现了基本两层神经网络，其中$x_i(i=1,2,3)$为输入层值，$a_i^{(k)}(k=1,2,\dots ,K;i=1,2,3,\dots ,N_k)$表示第k层中，第i个神经元的激活值，$N_k$表示第k层的神经元个数。当k=1时，即为输入层，即$a_i^{(1)}=x_i$，而$x_0=1$和$a_0^{(2)}=1$为偏置项

为了求最后的输出值$h_{\theta }(x)=a_1^{(3)}$，我们需要计算隐藏层中每个神经元的激活值$a_{ji}^{(k)}(k=2,3)$，而隐藏层/输出层的每一个神经元，都是由上一层神经元经过类似逻辑回归计算得到。

反向传播（BP算法）

给出一个示例，是我们的作业题目

（1）在该例子中什么是输入层，隐藏层，输出层，并对不同的层和层之间的权重矩阵进行维度标记。

（2）使用链式法则，在损失函数L上，分别对$z^{[2]}，z_1^{[1]}，z_2^{[1]}，x_1，x_2$，进行求偏导

解

（1）

输入层：$x_1,x_2$，维度为$2\times 1$;

输入层与隐藏层之间的权重矩阵：$w_{11}^{[1]},w_{12}^{[1]}，w_{21}^{[1]},w_{22}^{[1]}$，维度为$2\times 2$;

经过加权求和与偏置后，得到：$z_1^{[1]},z_2^{[1]}$，维度为$2\times 1$;

经过ReLU激活函数后得到隐藏层：$a_1^{[1]},a_2^{[1]}$，维度为$2\times 1$;

隐藏层与输出层之间的权重矩阵：$w_{11}^{[2]},w_{12}^{[2]}$，维度为$1\times 2$;

经过加权求和与偏置后，得到：$z^{[2]}$，维度为$1\times 1$;

经过sigmoid激活函数后得到输出层：$a^{[2]}$，维度为$1\times 1$。

（2）

损失函数：

$$L=-[y\log a^{[2]}+(1-y)\log (1-a^{[2]})]$$

所有表达式：

$$\begin{array}{rl}{a}^{[2]}& =\sigma (z^{[2]})\\ z^{[2]}& =w_{11}^{[2]}{a}_1^{[1]}+w_{12}^{[2]}{a}_2^{[1]}+b_1^{[2]}\\ a_1^{[1]}& =ReLU(z_1^{[1]})\\ a_2^{[1]}& =ReLU(z_2^{[1]})\\ z_1^{[1]}& =w_{11}^{[1]}{x}_1+w_{12}^{[1]}{x}_2+b_1^{[1]}\\ z_2^{[1]}& =w_{21}^{[1]}{x}_1+w_{22}^{[1]}{x}_2+b_2^{[1]}\end{array}$$

阶段求导：

$$\begin{array}{rl}\frac{\partial L}{\partial a^{[2]}}& =-[\frac{y}{a^{[2]}}+\frac{y-1}{1-a^{[2]}}]\\ \frac{\partial a^{[2]}}{\partial z^{[2]}}& =\sigma (z^{[2]})(1-\sigma (a^{[2]}))=a^{[2]}(1-a^{[2]})\\ \frac{\partial z^{[2]}}{\partial a_1^{[1]}}& =w_{11}^{[2]}\\ \frac{\partial z^{[2]}}{\partial a_2^{[1]}}& =w_{12}^{[2]}\\ \frac{\partial a_1^{[1]}}{\partial z_1^{[1]}}& =\{\begin{array}{l}0,\text{for }{z}_1^{[1]}<0\\ 1,\text{for }{z}_1^{[1]}\ge 0\end{array}\\ \frac{\partial a_1^{[1]}}{\partial z_2^{[1]}}& =\{\begin{array}{l}0,\text{for }{z}_2^{[1]}<0\\ 1,\text{for }{z}_2^{[1]}\ge 0\end{array}\\ \frac{\partial z_1^{[1]}}{\partial x_1}& =w_{11}^{[1]},\frac{\partial z_1^{[1]}}{\partial x_2}=w_{12}^{[1]},\frac{\partial z_2^{[1]}}{\partial x_1}=w_{21}^{[1]},\frac{\partial z_2^{[1]}}{\partial x_2}=w_{22}^{[1]}\end{array}$$

链式求导：